
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование второго уравнения системы с учетом начальногоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
т.е. показывает, что магнитное поле не влияет на компоненту скорости электрона в направлении силовых линий поля. Совместное решение первого и третьего уравнений системы, состоящее в дифференцировании первого по времени и подстановке значения dvz /dt из третьего, приводит к уравнению, связывающему скорость электрона vx со временем:
где Решение уравнений такого типа можно представить в виде:
причем из начальных условий при t=0, v x=vx0, dvx/dt=0 (что следует из первого уравнения системы, так как vz0 = 0) вытекает, что
Кроме того, дифференцирование этого уравнения с учетом первого уравнения системы приводит к выражению:
Заметим, что возведение в квадрат и сложение двух последних уравнений дает выражение:
которое еще раз подтверждает, что магнитное поле не изменяет величины полной скорости (энергии) электрона. В результате интегрирования уравнения, определяющего его vx, получаем:
постоянная интегрирования в соответствии с начальными условиями равна нулю. Интегрирование уравнения, определяющего скорость vz с учетом того, что при z = 0, t = 0 позволяет найти зависимость от времени координаты z электрона:
Решая два последних уравнения относительно квадрат и складывая, после несложных преобразований получаем уравнение проекции траектории электрона на плоскости XOZ:
Это уравнение окружности радиуса 22. Оптико-механическая аналогия, электронно-оптический показатель преломления. Оптико-механическая аналогия - это сходство траектории движения частицы в потенциальном силовом поле с траекторией лучей в оптически неоднородной среде. Траектория материальной точки и траектория светового луча совпадают при определенном соответствии потенциальной энергии и переменного в пространстве показателя преломления среды. Практическое значение оптико-механической аналогии связано с использованием ее в электронной оптике, которая занимается формированием и фокусировкой пучков электронов (или ионов) для получения с их помощью изображений и созданием на этой основе электронных и ионных микроскопов и проекторов. Электронно-оптич. показатель преломления п = р/р 0 в электрич. поле зависит только от координат, и такая среда для распространения электронных пучков изотропна. При наличии магн. поля (совместно с электрическим или без него) среда анизотропна, т. к. в этом случае п зависит ещё и от направления движения электронов, тогда
где т 0 - масса покоя электрона
23.
Движение заряженных частиц в электрическом и магнитном поле в веществе. Эффект Холла.
Электрический ток в вакууме. Виды электронных и ионных эмиссий. Классическое представление работы выходы электронов из твердых тел, как работа против сил зеркального изображения электрона в металлических проводниках. Для получения электрического тока в вакууме необходимо наличие свободных носителей. Получить их можно за счет испускания электронов металлами - электронной эмиссии. Виды эмиссий: · Термоэлектронная · Фотоэлектронная · Вторичная электронная · Вторичная ионно-ионная · Термоионная · Горячих электронов
26. Термоэлектронная эмиссия. Основное уравнение ТЭЭ
27. Эффект Шоттки. Влияние поправки Шоттки на ТЭЭ. Эмиссии электронов из металла препятствует потенциальный барьер, образованный из электрических сил изображения. Снижение этого барьера по мере увеличения прилагаемого внешнего электрического поля называется эффектом Шоттки. Рассмотрим сначала систему металл-вакуум. Минимальная энергия, которую необходимо передать электрону на уровне Ферми чтобы он покинул металл, называется работой выхода Электрон, который находится в условиях вакуума на некотором расстоянии
где
Эта работа отвечает потенциальной энергии электрона на расстоянии Если в системе есть внешнее электрическое поле
Снижение барьера Шоттки
Из этих уравнений находим значение снижения барьера и расстояние: Полученные выше результаты могут быть перенесены на системы металл-полупроводник. В данном случае электрическое поле
Значение ( Эффективная диэлектрическая проницаемость Эффект Шоттки используется в полупроводниковой технике и реализован в т. н. диодах Шоттки, имеющих высокие частотные характеристики.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.130.228 (0.008 с.) |

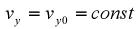
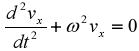
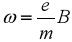 .
.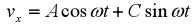
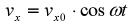
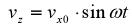
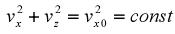
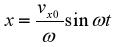 ,
,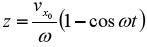
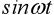 и
и 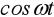 , возводя в
, возводя в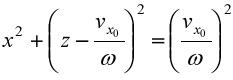
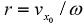 , центр которой расположен на оси z на расстоянии r от начала координат (рис. 2.2). Сама траектория электрона представляет собой цилиндрическую спираль радиуса
, центр которой расположен на оси z на расстоянии r от начала координат (рис. 2.2). Сама траектория электрона представляет собой цилиндрическую спираль радиуса  . Из полученных уравнений очевидно также, что величина
. Из полученных уравнений очевидно также, что величина 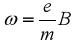 представляет собой круговую частоту движения электрона по этой траектории.
представляет собой круговую частоту движения электрона по этой траектории.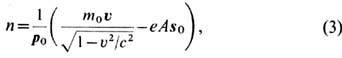












 (
( измеряется в электрон-вольтах). Для типичных металлов величина
измеряется в электрон-вольтах). Для типичных металлов величина 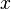 от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду
от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду 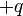 , который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна:
, который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна: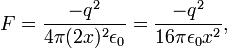
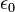 — диэлектрическая проницаемость вакуума. Работа, которую нужно совершить чтобы переместить электрон из точки
— диэлектрическая проницаемость вакуума. Работа, которую нужно совершить чтобы переместить электрон из точки 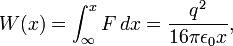
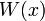 , обычно изображается на диаграммах прямой линией.
, обычно изображается на диаграммах прямой линией.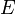 , то потенциальная энергия электрона
, то потенциальная энергия электрона 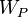 будет равна сумме:
будет равна сумме: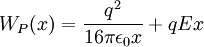 эВ.
эВ.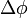 и расстояние
и расстояние  , при котором величина потенциала достигает максимума, определяется из условия
, при котором величина потенциала достигает максимума, определяется из условия 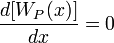 . Откуда находим:
. Откуда находим: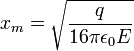 см,
см,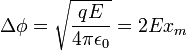 В.
В.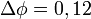 В,
В, 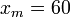 При
При 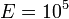 1/см и
1/см и 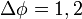 В,
В, 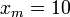 При
При 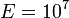 В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии
В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии 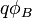 уменьшается.
уменьшается.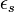 ), то есть:
), то есть: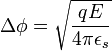
 для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 - 12,5. При
для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 - 12,5. При 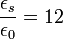 расстояние
расстояние 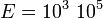 В/см. Если учесть, что скорость носителей около
В/см. Если учесть, что скорость носителей около 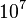 см/с, их время пролёта будет
см/с, их время пролёта будет 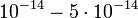 с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм). Поскольку диэлектрическая проницаемость кремния практически постоянна в диапазоне частот от нуля, соответствующей длине волны
с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм). Поскольку диэлектрическая проницаемость кремния практически постоянна в диапазоне частот от нуля, соответствующей длине волны 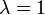 , в пролёта электрона через обеднённый слой решётка успевает поляризоваться. Поэтому значение диэлектрической проницаемости, полученные в фотоэлектрических и оптических опытах, близки друг к другу. Германий и арсенид галлия имеют аналогичные частотные зависимости диэлектрической проницаемости. Поэтому можно предположить, что в случае этих полупроводников значение диэлектрической проницаемости, определяющего силы изображения, в указанном выше интервале полей примерно совпадает со статичными значениями.
, в пролёта электрона через обеднённый слой решётка успевает поляризоваться. Поэтому значение диэлектрической проницаемости, полученные в фотоэлектрических и оптических опытах, близки друг к другу. Германий и арсенид галлия имеют аналогичные частотные зависимости диэлектрической проницаемости. Поэтому можно предположить, что в случае этих полупроводников значение диэлектрической проницаемости, определяющего силы изображения, в указанном выше интервале полей примерно совпадает со статичными значениями.


