
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной форме. Уравнения связи.Стр 1 из 4Следующая ⇒
Система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной форме. Уравнения связи.
Уравнения связи:
2. Методы расчета электрических полей дискретных зарядов. Поле двух точечных зарядов, поле диполя.
Поле двух точечных заряда для умных:
Пишем закон Кулона:
Для каждого зарядов. Пишем теорему косинусов для зарядов, теорему косинусов для расстояния между зарядами и расстоянием между зарядом и точкой (на рис. т. α). Из второго уравнения находим косинус и его подставляем в первое уравнение, затем находим общую напряженность.
Поле диполя:
Диполь во внешнем электрическом поле.
4. Расчет электрических полей методом «зеркального» изображения.
Теорема Гаусса для электрического поля. Поле равномерно заряженного цилиндра. Поле объемно заряженного шара.
Цилиндр:
Шар:
Дополнение:
Магнитное поле на оси кругового витка с током. Согласно закону Био-Савара-Лапласа, индукция магнитного поля, создаваемого элементом тока dl на расстоянии r от него есть
где В нашем случае α = π/2, sin α = 1; Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка:
Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR:
или, подставив значение r:
· Индукция магнитного поля в произвольной точке А, созданного отрезком проводника с током где
9, 10. Теорема о циркуляции векторов В и Н (закон полного тока). Магнитное поле бесконечно длинного соленоида. Магнитное поле тороида.
Электрическое поле в веществе. Поляризация диэлектриков. Три группы поляризации.
Характеристики поля поляризации. Связь векторов D, E, P. Теорема Гаусса для электрического поля в диэлектриках.
Условия на границе двух диэлектриков. Закон преломления векторов E и D.
14. Сегнетоэлектрики. Зависимости P(E), D(E), ε(E). Гистерезис. Пьезоэффект.
Намагниченность, магнитная восприимчивость. Связь B, J, H.
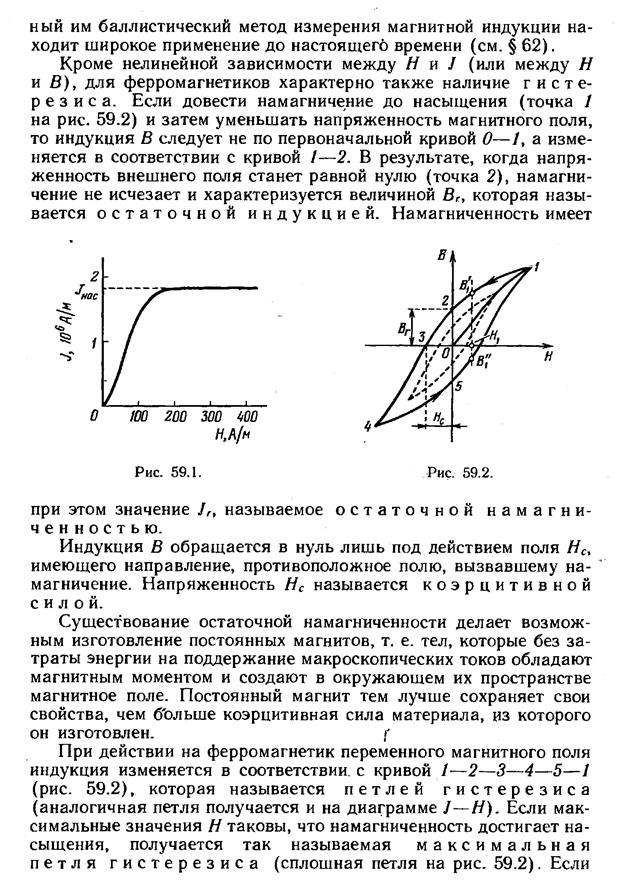
17. Ферромагнетики. Зависимости J(H), B(H), μ(Н). Гистерезис. Энергия, выделяемая в ферромагнетиках при перемагничивании.
Условия на границе двух магнетиков, закон преломления векторов Н и В. Магнитная защита, лабораторные магниты.
МАГНИТНОЕ ЭКРАНИРОВАНИЕ (магнитная защита) - защита объекта от воздействия магн. полей (постоянных и переменных). Совр. исследования в ряде областей науки (физика, геология, палеонтология, биомагнетизм) и техники (космич. исследования, атомная энергетика, материаловедение) часто связаны с измерениями очень слабых магн. полей ~10-14-10-9 Тл в широком частотном диапазоне. Внешние магнитные поля (например, поле Земли
Экранирующее действие полого цилиндра из ферромагнитного вещества с Движение заряженных частиц в электрическом и магнитном поле в веществе. Эффект Холла.
Электрический ток в вакууме. Виды электронных и ионных эмиссий. Классическое представление работы выходы электронов из твердых тел, как работа против сил зеркального изображения электрона в металлических проводниках.
Для получения электрического тока в вакууме необходимо наличие свободных носителей. Получить их можно за счет испускания электронов металлами - электронной эмиссии. Виды эмиссий: · Термоэлектронная · Фотоэлектронная · Вторичная электронная · Вторичная ионно-ионная · Термоионная · Горячих электронов
26. Термоэлектронная эмиссия. Основное уравнение ТЭЭ
27. Эффект Шоттки. Влияние поправки Шоттки на ТЭЭ. Эмиссии электронов из металла препятствует потенциальный барьер, образованный из электрических сил изображения. Снижение этого барьера по мере увеличения прилагаемого внешнего электрического поля называется эффектом Шоттки. Рассмотрим сначала систему металл-вакуум. Минимальная энергия, которую необходимо передать электрону на уровне Ферми чтобы он покинул металл, называется работой выхода Электрон, который находится в условиях вакуума на некотором расстоянии
где
Эта работа отвечает потенциальной энергии электрона на расстоянии Если в системе есть внешнее электрическое поле
Снижение барьера Шоттки
Из этих уравнений находим значение снижения барьера и расстояние: Полученные выше результаты могут быть перенесены на системы металл-полупроводник. В данном случае электрическое поле
Значение (
Эффективная диэлектрическая проницаемость Эффект Шоттки используется в полупроводниковой технике и реализован в т. н. диодах Шоттки, имеющих высокие частотные характеристики. Система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной форме. Уравнения связи.
Уравнения связи:
2. Методы расчета электрических полей дискретных зарядов. Поле двух точечных зарядов, поле диполя.
Поле двух точечных заряда для умных:
Пишем закон Кулона:
Для каждого зарядов. Пишем теорему косинусов для зарядов, теорему косинусов для расстояния между зарядами и расстоянием между зарядом и точкой (на рис. т. α). Из второго уравнения находим косинус и его подставляем в первое уравнение, затем находим общую напряженность.
Поле диполя:
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.130 (0.045 с.) |



























 ,
, α – угол между элементом тока
α – угол между элементом тока  и радиус-вектором
и радиус-вектором  , проведенным из этого элемента в точку наблюдения; r - расстояние от элемента тока до точки наблюдения.
, проведенным из этого элемента в точку наблюдения; r - расстояние от элемента тока до точки наблюдения. , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы
, где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы  образуют в этой точке конус с углом раствора при вершине 2
образуют в этой точке конус с углом раствора при вершине 2 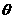 = π - 2β, где β – угол между отрезками а и r.
= π - 2β, где β – угол между отрезками а и r. .
.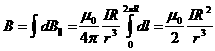
 .
. конечной длины,
конечной длины, , (3)
, (3) – расстояние от т. А до проводника;
– расстояние от т. А до проводника;  – углы, образованные радиус-вектором, проведенном в т.А соответственно из начала и конца проводника, с направлением тока.
– углы, образованные радиус-вектором, проведенном в т.А соответственно из начала и конца проводника, с направлением тока.


















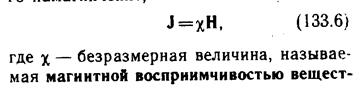









 Тл с шумом
Тл с шумом  Тл, магн. шумы от электрич. сетей и городского транспорта) создают сильные помехи для работы высокочувствит. магнитометрич. аппаратуры. Уменьшение влияния магн. полей в сильной степени определяет возможности проведения магн. измерений Среди методов М. э. наиболее распространены следующие.
Тл, магн. шумы от электрич. сетей и городского транспорта) создают сильные помехи для работы высокочувствит. магнитометрич. аппаратуры. Уменьшение влияния магн. полей в сильной степени определяет возможности проведения магн. измерений Среди методов М. э. наиболее распространены следующие.
 (1 - внеш. поверхность цилиндра, 2 -внутр. поверхность). Остаточное магнитное
(1 - внеш. поверхность цилиндра, 2 -внутр. поверхность). Остаточное магнитное  поле внутри цилиндра
поле внутри цилиндра







 (
( измеряется в электрон-вольтах). Для типичных металлов величина
измеряется в электрон-вольтах). Для типичных металлов величина 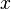 от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду
от поверхности металла, индуцирует на поверхности положительный заряд. Сила притяжения между электроном и этим индуцированным поверхностным зарядом равна по величине силе притяжения к эффективному положительному заряду 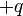 , который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна:
, который называют зарядом изображения. Эта сила, которая также называется силой изображения, равна: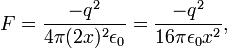
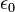 — диэлектрическая проницаемость вакуума. Работа, которую нужно совершить чтобы переместить электрон из точки
— диэлектрическая проницаемость вакуума. Работа, которую нужно совершить чтобы переместить электрон из точки 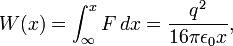
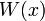 , обычно изображается на диаграммах прямой линией.
, обычно изображается на диаграммах прямой линией.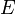 , то потенциальная энергия электрона
, то потенциальная энергия электрона 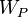 будет равна сумме:
будет равна сумме: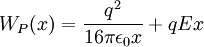 эВ.
эВ.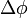 и расстояние
и расстояние  , при котором величина потенциала достигает максимума, определяется из условия
, при котором величина потенциала достигает максимума, определяется из условия 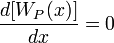 . Откуда находим:
. Откуда находим: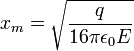 см,
см,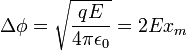 В.
В.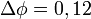 В,
В, 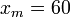 При
При 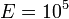 1/см и
1/см и 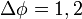 В,
В, 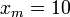 При
При 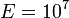 В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии
В/см. В результате, сильное электрическое поле вызывает значительное снижение барьера Шоттки. Вследствие этого эффективная работа выхода из металла для термоэлектронной эмиссии 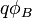 уменьшается.
уменьшается.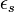 ), то есть:
), то есть: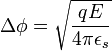
 для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 - 12,5. При
для контакта золото-кремний определённая по результатам фотоэлектрических измерений. На практике имеем, что эффективная диэлектрическая проницаемость сил изображения находится в диапазоне 11,5 - 12,5. При 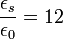 расстояние
расстояние 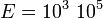 В/см. Если учесть, что скорость носителей около
В/см. Если учесть, что скорость носителей около 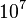 см/с, их время пролёта будет
см/с, их время пролёта будет 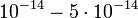 с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм). Поскольку диэлектрическая проницаемость кремния практически постоянна в диапазоне частот от нуля, соответствующей длине волны
с. Оказывается, что диэлектрическая проницаемость, полученная при учёте силы изображения, близко к значений проницаемости (~12) для электромагнитного излучения соответствующих частот (с длиной волны 3-15 мкм). Поскольку диэлектрическая проницаемость кремния практически постоянна в диапазоне частот от нуля, соответствующей длине волны 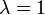 , в пролёта электрона через обеднённый слой решётка успевает поляризоваться. Поэтому значение диэлектрической проницаемости, полученные в фотоэлектрических и оптических опытах, близки друг к другу. Германий и арсенид галлия имеют аналогичные частотные зависимости диэлектрической проницаемости. Поэтому можно предположить, что в случае этих полупроводников значение диэлектрической проницаемости, определяющего силы изображения, в указанном выше интервале полей примерно совпадает со статичными значениями.
, в пролёта электрона через обеднённый слой решётка успевает поляризоваться. Поэтому значение диэлектрической проницаемости, полученные в фотоэлектрических и оптических опытах, близки друг к другу. Германий и арсенид галлия имеют аналогичные частотные зависимости диэлектрической проницаемости. Поэтому можно предположить, что в случае этих полупроводников значение диэлектрической проницаемости, определяющего силы изображения, в указанном выше интервале полей примерно совпадает со статичными значениями.


