
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие абсолютно твердого тела. Поступательное, вращательное и плоско-параллельное движение твердого тела. Связь между угловой и линейной скоростями твердого тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Твердое тело (абсолютно твердое тело) – это тело, которое ни при каких условиях не может деформироваться; в абсолютно твердом теле при всех условиях расстояние между точками остается постоянным.
Поступательное движение твердого тела – движение, при котором линия, соединяющая любые две точки тела, сохраняет неизменное направление в пространстве. При поступательном движении любая линия переносится параллельно самой себе, т.е. смещение всех точек тела одинаково. Поэтому при поступательном движении все точки твердого тела обладают одинаковыми линейными скоростями и одинаковыми линейными ускорениями.
Вращательное движение – движение, при котором траекторией всех точек являются концентрические окружности с центрами на одной прямой, называемой осью вращения. Концентрические окружности – окружности, у которых один центр.При вращательно движении все точки данного тела обладают одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями.
Линейные скорости вращающегося тела одинаковы: чем дальше от оси вращения отстоит точка, тем большей линейной скоростью она обладает. Плоскопараллельное движение – движение, при котором любая точка твердого тела во время движения остается в одной из параллельных плоскостей.
Связь между линейной и угловой скоростями:
Билет 6. Центр инерции твердого тела. Связь координат и масс твердого тела в системе координат, связанной с центром масс (лемма о центре масс). Координаты центра инерции. Закон движение центра инерции твердого тела.
Если укрепить тело в центре тяжести, то оно будет находиться в равновесии при любом положении тела, т.е. сумма моментов сил тяжести всех частиц тела относительно любой горизонтальной оси, проходящей через центр тяжести, будет равна нулю.
Если повернуть тело относительное оси
а)
б) ex – external – внешний in – internal – внутренний
Центр инерции твердого тела движется так, как если бы к нему были приложены все внешние силы и масса, всего тела была бы сосредоточена в центре масс.
Билет 7. Момент силы. Закон динамики вращения тела вокруг неподвижной оси (уравнение вращательного движения). Момент инерции.
Момент инерции зависит не только от величины массы тела, но и от распределения масс относительно оси.
Уравнение вращательного движения является аналогом II-го закона Ньютона. Что бы вызвать поступательное движение точки, нужно приложить силу; чтобы получить вращательное движение тела, необходимо приложить момент силы. Так же как сила вызывает линейное ускорение, так и момент силы вызывает появление углового ускорения. Коэффициентами в этих уравнениях является масса и момент инерции. Значит, масса является мерой инерции для поступательного движения, а момент инерции является мерой инерции для вращательного движения.
Билет 8. Момент импульса. Уравнение моментов (относительно оси). Закон сохранения момента импульса.
Если Закон сохранения момента импульса: Момент импульса твердого тела остается постоянным, если суммарный момент внешних сил равен нулю.
Билет 9. Момент импульса и момент силы относительно точки. Уравнение моментов (относительно точки).
Связь моментов относительно точки и моментов относительно оси: Момент силы, относительно оси есть проекция момента силы относительно точки на эту ось; при этом полюс должен лежать на оси вращения. Такая же связь существует между моментом относительно точки и моментом относительно оси.
Получим уравнение моментов относительно точки в случае плоского движения.
{левая часть}=
Билет 10.
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.248.129 (0.01 с.) |

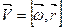
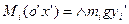
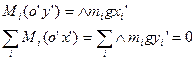
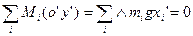
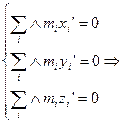
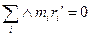 - лемма о центре масс
- лемма о центре масс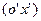 на
на  по часовой стрелке, то ось
по часовой стрелке, то ось 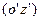 займет положение
займет положение  , и плечом силы тяжести относительно
, и плечом силы тяжести относительно 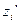 , т.е
, т.е 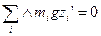
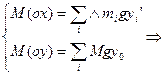

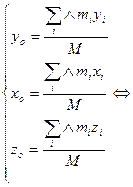
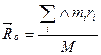
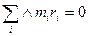 - саму произведения центра масс тела на его радиус-вектор.
- саму произведения центра масс тела на его радиус-вектор.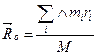
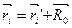
 , (
, ( - скорость движения системы отсчета относительно другой.)
- скорость движения системы отсчета относительно другой.)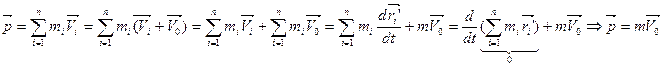 (масса всей системы на скорость центра масс)
(масса всей системы на скорость центра масс)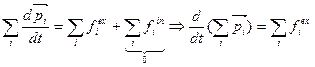

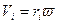 ,
, 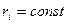
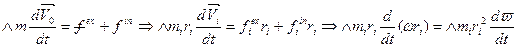
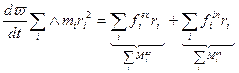 ,
, 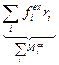 =0
=0 -уравнение вращательного движения
-уравнение вращательного движения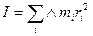 -момент инерции
-момент инерции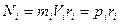 - момент импульса точки относительно оси
- момент импульса точки относительно оси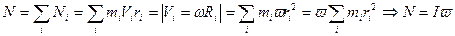 - момент импульса тела относительно оси
- момент импульса тела относительно оси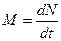 - уравнение моментов (относительно оси)
- уравнение моментов (относительно оси)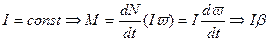

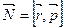
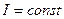
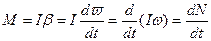
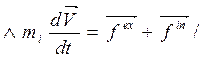 на
на  слева
слева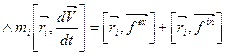
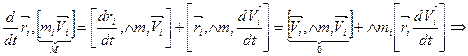
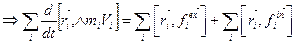
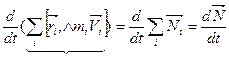
 - уравнение моментов относительно точки.
- уравнение моментов относительно точки.


