Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная формула теории управления с обратной связью и ее приложения. Мультипликатор Кейнса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть обратная связь осуществляется с коррекцией сигнала на основе дополнительного элемента системы - регулятора (корректора)
Схема 8. Управление с обратной связью и регулятором. Т.о., входной поток теперь увеличивается и становится
Формула (1) – основная формула теории регулирования.
Схема 9. Система с контуром Схема системы с обратной связью любой сложности представима в виде трех элементов: контура, последовательного соединения узлов и параллельного. В случае последовательного соединения имеем
При параллельном соединении узлов сложной системы:
Рассмотрим случай, когда
Получаем Т.о. для нелинейной зависимости мы получаем аналоговую формулу теории управления с обратной связью для скоростей изменения входного и выходного потоков( Мультипликатор Кейнса. Рассмотрим систему, состоящую из объекта управления (ОУ), субъекта управления (СУ) и внешней среды.
Из внешней среды в ОУ под наблюдением СУ направляются ресурсы в размере Пусть на ОУ поступают определенные финансовые ресурсы где Т.о.
Схема системы имеет вид
Схема 9. Мультипликатор Кейнса Т.о. основная формула теории регулирования (1) в данном случае записывается
Пример 1. Рассмотрим экономическую систему, в которой предполагается, что экономический цикл повторяется неограниченное число раз. Кроме того, в каждом периоде инвестиции постоянны и равны
…
Тогда предельный прирост конечного продукта рассчитывается по основной формуле теории регулирования Данная модель предложена Каном и Кларком. Пример 2. Рассмотрим модель Леонтьева в матричном виде Очевидно, что функционирование экономической системы, описываемой моделью Леонтьева, может быть представлена следующей схемой с контуром
Пример 3. Экономическая система выпускает продукцию Выпишем модель, соответствующую сформулированной задаче.
Полученная модель называется моделью Лурье. Рассчитаем мультипликатор Кейнса. Пример 4. Найдите коэффициент усиления системы, заданной схемой
Обозначим
Задачи 1. Рассматривается система с контуром. Коэффициент усиления входного сигнала 2. Необходимо с помощью контура усилить сигнал в
3. Найдите коэффициент усиления системы, заданной схемой
4. Найдите коэффициент усиления системы, заданной схемой
5. Рассчитайте предельную склонность к потреблению и мультипликатор Кейнса по модели Лурье для отрасли «Сельское хозяйство» Воронежской области, если известны следующие характеристики отрасли: производственная функция – функция Кобба-Дугласа
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.112.243 (0.01 с.) |

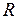 .
.
 . Считая, что
. Считая, что  и
и  :
: ,если
,если  , то
, то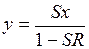 . (1)
. (1) , где
, где - коэффициент усиления новой системы, влияние преобразователя на вход. Новая система
- коэффициент усиления новой системы, влияние преобразователя на вход. Новая система 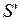 представлена на схеме 8 – такое соединение элементов назовем контуром
представлена на схеме 8 – такое соединение элементов назовем контуром
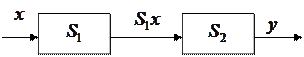
 .
.
 .
. ,
,  ,
,  - функции, зависящие от времени,
- функции, зависящие от времени,  - нелинейные, гладкие функции. Нелинейная зависимость сводится к основной теории в терминах производной.
- нелинейные, гладкие функции. Нелинейная зависимость сводится к основной теории в терминах производной. ,
,  .
. .
. ).
).
 ,
,  - входной поток от СУ к ОУ.
- входной поток от СУ к ОУ. , которые используются на накопление (капиталовложение)
, которые используются на накопление (капиталовложение)  и потребление
и потребление  :
:  . Тогда прирост финансовых ресурсов распределяется следующим образом
. Тогда прирост финансовых ресурсов распределяется следующим образом  , в то же время финансовые ресурсы увеличиваются при увеличении инвестиций
, в то же время финансовые ресурсы увеличиваются при увеличении инвестиций  ,
,  - величина прироста финансового ресурса приходящегося на единицу прироста накоплений. Получаем
- величина прироста финансового ресурса приходящегося на единицу прироста накоплений. Получаем  ,
,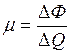 - предельная склонность к потреблению, доля прироста потребления во всем приросте финансов.
- предельная склонность к потреблению, доля прироста потребления во всем приросте финансов.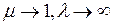 , т.е. увеличивая долю потребления, мы повышаем эффективность инвестиций – парадокс Кейнса. Величина
, т.е. увеличивая долю потребления, мы повышаем эффективность инвестиций – парадокс Кейнса. Величина  - мультипликатор Кейнса. Чем больше предельная склонность к потреблению, тем выше коэффициент мультипликации. Величина мультипликации — это результат прироста доходов и соответственно спроса в инвестиционных и сопряженных с ними отраслях.
- мультипликатор Кейнса. Чем больше предельная склонность к потреблению, тем выше коэффициент мультипликации. Величина мультипликации — это результат прироста доходов и соответственно спроса в инвестиционных и сопряженных с ними отраслях.
 (2).
(2). , а потребление составляет постоянную долю (
, а потребление составляет постоянную долю (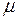 ) от конечного продукта
) от конечного продукта  , произведенного в предыдущем периоде.
, произведенного в предыдущем периоде. ,
, ,
, ,
, ,
, .
. .
.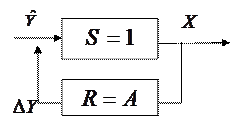

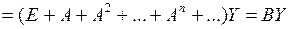 ,здесь
,здесь 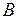 -матрица полных затрат.
-матрица полных затрат.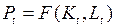 , используя основной капитал
, используя основной капитал  и трудовые ресурсы
и трудовые ресурсы  . Финансовый ресурс на начало года формирует основной капитал и потребление в году
. Финансовый ресурс на начало года формирует основной капитал и потребление в году 
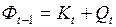 . С другой стороны, финансовый ресурс в конце года учитывает выпущенную в году
. С другой стороны, финансовый ресурс в конце года учитывает выпущенную в году  и капитал
и капитал  . Прирост финансовых средств пропорционален приросту капитала
. Прирост финансовых средств пропорционален приросту капитала  . Необходимо рассчитать мультипликатор Кейнса.
. Необходимо рассчитать мультипликатор Кейнса.



 ,
,  - предельная склонность к потреблению (доля прироста потребления в приросте финансовых средств).
- предельная склонность к потреблению (доля прироста потребления в приросте финансовых средств).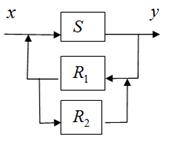
 - подсистему из усилителей
- подсистему из усилителей  , тогда для системы
, тогда для системы  . Для исходной системы подсистема
. Для исходной системы подсистема  .
. . Каким должен быть усилитель
. Каким должен быть усилитель 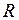 , чтобы входной сигнал усиливался в 100 раз.
, чтобы входной сигнал усиливался в 100 раз. раз, при этом плата за усиление в системе
раз, при этом плата за усиление в системе  , в регуляторе -
, в регуляторе -  . Каковы оптимальные усиления
. Каковы оптимальные усиления 
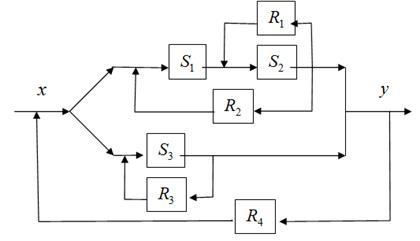
 с параметрами
с параметрами  ,
,  ,
,  .
.  тыс.руб. Ресурсы отрасли приведены в таблице (в тыс.руб.).
тыс.руб. Ресурсы отрасли приведены в таблице (в тыс.руб.).