
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические системы: сущность, структура, классификация, способы описания. Система как черный ящик.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Систему будем называть динамической, если параметры, характеристики, переменные, которые используются при ее описании, либо в явном виде зависят от времени, либо являются дискретными, меняющимися во времени величинами. При описании динамических систем вводится системное время Описатель динамической системы имеет вид
где
Начальное состояние системы
Схема 2. Простейшая модель динамической системы.
Схема 3. Модель динамической системы с задержкой выходного потока
Схема 4. Модель динамической системы со складом Т.о. видно, что описателю динамической системы могут соответствовать различные схемы функционирования системы. Кроме того, описатель используется для разработки модели динамической системы. Математически модель динамической системы представляется в виде а) задачи динамического программирования, б) задачи оптимального управления. Динамическое программирование – метод решения задач с оптимальной подструктурой и перекрывающимися подзадачами, который эффективнее, чем решение впрямую. Оптимальная подструктура – оптимальное решение подзадач меньшего размера, который может быть использован для решения исходной задачи. При решении задача разбивается на подзадачи, и решение каждой о переводе системы (нахождении управляющего воздействия) в новое состояние зависит только от текущего состояния и не зависит от предыстории (принцип Белмана). Постановка задачи динамического программирования:
В качестве функции цели чаще всего рассматривают некоторый обобщенный критерий: 1) 2) периода Решением данной задачи является вектор состояний системы При построении модели в виде задачи оптимального управления, необходимо знать закон, по которому происходит изменение величины
Функция цели
где Для решения задачи управления используется принцип максимума Понтрягина. На основе задачи управления строится функция Гамильтона, выписывается нормальное уравнение и получается нормальная система. После решения системы определяется точка, которая является необходимой точкой, доставляющей максимум функции цели. Система как черный ящик Рассмотрим функционирующую систему, реализующую свою миссию, для которой определены входы, выходы, но неизвестен закон преобразования входов в выходы, неизвестна передаточная функция. Для управления такой системой необходимо найти вид передаточной функции. С этой целью создается статистика накопления входных потоков Если потребовать, чтобы эта функция совпадала со статистическими данными, то можно подобрать множество таких функций. Т.о. при восстановлении функции, необходимо - выбрать класс аппроксимирующих функций, - точность аппроксимации, - критерий согласия между функцией и статистическими данными. Обычно на практике используют следующие классы функций: 1)линейные комбинации функций 1, x, x2,..., xn, т.е. функции из класса полиномов степени не выше n (аппроксимация алгебраическим многочленом заданной степени); 2)линейные комбинации функций Sin(akx) и Cos(akx) (аппроксимация тригонометрическим многочленом, или отрезком ряда Фурье); 3)комбинации экспоненциальных функций Exp( 4) классы функций, удовлетворяющие ранее заданным свойствам (производственные функции, функция затрат и т.д.) В качестве критерия согласия используют три условия: 1)точное совпадение значений искомой функции со статистическими данными (критерий интерполяции); 2)сумма квадратов отклонений значений искомой функции и заданных значений должна быть минимальной (критерий среднеквадратической аппроксимации);
3)максимальное по абсолютной величине из отклонений значений искомой функции заданных значений должно быть минимальным (критерий равномерной аппроксимации). Если же об аналитическом виде функции ничего неизвестно, то, полагая, что она является непрерывной функцией, вид ее можно найти, используя теорему Колмогорова. Теорема Колмогорова. Любая непрерывная функция от n переменных
При всей своей математической красоте теорема Колмогорова малоприменима на практике. Это связано с тем, что функции hij — негладкие и трудно вычислимые; также неясно, каким образом можно подбирать функции gj для данной функции F. Роль этой теоремы состоит в том, что она показала принципиальную возможность реализации сколь угодно сложных зависимостей с помощью относительно простых автоматов, например, нейронных сетей. Т.о., если система описана как черный ящик, и необходимо знать аналитический вид передаточной функции системы, то его можно восстановить по статистике функционирования системы. Другим способом является структурирование системы, т.е. введение элементов и связей между ними. Целевые структурированные системы описываются следующим образом
Цель системы может быть задана не функциональной зависимостью, а конечным целевым состоянием системы. Пусть
Путь, по которому развивается система в период времени Задача исследования целевой структурированной системы состоит в поиске такой траектории, благодаря которой будут использованы имеющиеся ресурсы и достигнуто максимальное значение выбранной цели. Каждой целевой системе можно поставить в соответствие модель:
Пример 1. Примером системы – черного ящика может служить экономический объект (предприятие, региональная экономика, экономика страны и т.д.), производящий некоторую продукцию или оказывающий услуги, использующий для этого определенные ресурсы. Пусть экономическая система выпускает один вид продукта. Если известны объем выпуска системы за некоторый период ( Основные свойства производственной функции: 1. Выпуск продукции равен нулю при отсутствии ресурсов и отсутствие только одного ресурса не дает выпуска продукции
2. При увеличении затрат или улучшении качества ресурсов выпуск продукции не уменьшается. Если ПФ непрерывно дифференцируема, то данное свойство записывается в виде 3. По мере увеличения количества одного ресурса при постоянных количествах других предельная эффективность использования этого ресурса не возрастает. Если ПФ дважды непрерывно дифференцируема, то данное свойство записывается в виде В исследованиях наиболее распространенными ПФ являются двухфакторные ПФ, отражающие зависимость объема выпуска от затрат двух факторов: трудовых ресурсов (
К основным видам ПФ можно отнести следующие: 1. Линейная 2. Кобба-Дугласа 3. ПФ с постоянной эластичностью замены (CES) Для восстановления аналитического вида линейной по параметрам ПФ и линеаризуемой (ПФ Кобба-Дугласа) используется метод наименьших квадратов (МНК), для других видов ПФ необходимо применение численных методов. Для восстановления аналитического вида ПФ Кобба-Дугласа МНК производят следующие преобразования:
Обозначим
Далее находят Пример 2. Пусть имеется
где В каждый момент времени распределяются дополнительные финансовые ресурсы Формирование капитала и труда в момент времени
Ограничение на дополнительный финансовый ресурс
Функция цели – максимизация суммарного выпуска всех отраслей за период времени
Модель (1)-(8) называется моделью Лисичкина. Данная задача – задача оптимального управления, которая решается составлением аналога функции Лейбница – Гамильтониана. Необходимо найти оптимальное управление, т.е. такое значение переменных Пример 3. Самолет находится на высоте Для решения задачи введем сетку изменения расстояния и скорости – разобьем интервал изменения скоростей Текущее состояние характеризуется парой
Т.о. получаем (0,0)-(0,1)-(1,1)-(2,1)-(2,2)-(2,3)-(2,4)-(3,4)-(4,4)-(5,4).
Пример 4. Проведено 15 экспериментов по измерению значений
Известно, что искомая функция принадлежит семейству функций F(x)= A·x + B/x. Найти параметры Будем решать данную задачу методом наименьших квадратов. Подберем параметры A и B так, чтобы обеспечить минимум суммы квадратов отклонений между экспериментальными значениями Yi и ожидаемыми (расчётными) значениями Yi =F(Xi):
В нашем случае так называемая остаточная дисперсия определяется выражением
Дифференцируя (1) по A и B, получаем систему уравнений
или
Введем следующие обозначения Тогда (3) можно записать в виде
Получили линейную систему из 2-х уравнений относительно 2-х неизвестных A и B. Главный определитель системы (4):
а вспомогательные
Тогда решение системы (4) можно найти по формулам Крамера:
Качество полученной аппроксимации определяется величиной остаточной дисперсии T(A,B) (чем ближе она к нулю, тем лучше подобранная зависимость аппроксимирует наблюдения). Далее необходимо подставить значения наблюдений в формулу (5) и найти численное значение параметров Задачи 1. Самолет находится на высоте а) б) в)
2. Найдите численное решение задачи из примера 4 п.1.3. 3. Проведено 15 экспериментов по отысканию значений линейной функции, получены следующие значения
Восстановите вид функции, используя метод наименьших квадратов. 4. Проведено 15 экспериментов по отысканию значений функции
Какая из функций точнее аппроксимирует функцию 5. Фирма выпускает продукцию, используя 2 основных ресурса: основные фонды и трудовые ресурсы. Найти, какая из ПФ: 1. Линейная 2. Кобба-Дугласа 3. Кобба-Дугласа с учетом НТП лучше описывает зависимость выпуска от затрачиваемых ресурсов, если известна история работы фирмы за 2 года: № п/п - № месяца,
Основы квалиметрии
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.6.24 (0.068 с.) |

 ,
,  - начальное время;
- начальное время;  - горизонт системного времени.
- горизонт системного времени. ,
, - простейший описатель системы, содержащий элементы, связи и структуру системы;
- простейший описатель системы, содержащий элементы, связи и структуру системы; - входной поток, заданный на множестве
- входной поток, заданный на множестве  ;
; - величина входа внешней среды,
- величина входа внешней среды,  - множество состояний, определяющее рамки, в которых система может существовать;
- множество состояний, определяющее рамки, в которых система может существовать; - выходной поток, рассчитываемый с помощью передаточной функции
- выходной поток, рассчитываемый с помощью передаточной функции  , зависящей от вектора состояний
, зависящей от вектора состояний  :
:  .
. считается заданным.
считается заданным.


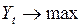 ,
, 


 ,
, 
 ,
, 
 .
.
 ,
,  - коэффициент предпочтения временного
- коэффициент предпочтения временного .
. ,
,  :
: .
. ,
,  - начальное состояния и начальное управление. Здесь
- начальное состояния и начальное управление. Здесь  - функция управления.
- функция управления. ,
, - функция качества,
- функция качества,  - оценка состояния. Функции
- оценка состояния. Функции  ,
,  полагаются такими, что интеграл существует.
полагаются такими, что интеграл существует. и соответствующих им выходных потоков
и соответствующих им выходных потоков  , т.е. история протекания процессов. Именно по этой информации восстанавливается аналитический вид функции
, т.е. история протекания процессов. Именно по этой информации восстанавливается аналитический вид функции  .
. kx) c вышеуказанными и некоторые другие;
kx) c вышеуказанными и некоторые другие; может быть представлена в виде суперпозиции
может быть представлена в виде суперпозиции  функции
функции , где
, где  и
и  - непрерывные функции, не зависящие от вида представляемой функции F.
- непрерывные функции, не зависящие от вида представляемой функции F.
 - функция цели.
- функция цели. - система в начальный момент времени,
- система в начальный момент времени, 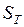 - характеристики конечной системы, целевое состояние системы.
- характеристики конечной системы, целевое состояние системы.
 , называется траекторией системы
, называется траекторией системы  .
. (
( )
)

 ) и затрачиваемые при этом ресурсы (
) и затрачиваемые при этом ресурсы (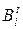 ,
,  ,
,  ), то передаточной функцией системы выступает производственная функция. Производственная функция (ПФ) представляет собой экономико-статистическую модель процесса производства продукции, отражающую устойчивую закономерную количественную зависимость между объёмным показателем ресурсов и максимально возможным выпуском при эффективном использовании ресурсов.
), то передаточной функцией системы выступает производственная функция. Производственная функция (ПФ) представляет собой экономико-статистическую модель процесса производства продукции, отражающую устойчивую закономерную количественную зависимость между объёмным показателем ресурсов и максимально возможным выпуском при эффективном использовании ресурсов. .
. ,
,  .
. ,
,  ) и основных фондов (
) и основных фондов ( ).
). ,
,  ,
, 
 ,
,  ,
, 
 ,
,  .
. ,
,

 ,
,  ,
,  ,
, .
. МНК и рассчитывают
МНК и рассчитывают  .
. отраслей (
отраслей ( ), производящих продукт в период времени
), производящих продукт в период времени  (1)
(1) - капитал,
- капитал,  - труд.
- труд. (их величина задана),
(их величина задана),  - доля, идущая в году
- доля, идущая в году  - доля финансовых ресурсов, идущая в году
- доля финансовых ресурсов, идущая в году 
 (2)
(2)
 ,
, 
 ,
, 
 ,
, 
 (6)
(6) (7)
(7) (8)
(8) , на которых Гамильтониан достигает своего максимума.
, на которых Гамильтониан достигает своего максимума. и летит со скоростью
и летит со скоростью  , необходимо рассчитать программу подъема самолета на высоту
, необходимо рассчитать программу подъема самолета на высоту  и развитие скорости
и развитие скорости  с минимальной затратой горючего, если задана норма расхода горючего при изменении высоты и неизменной скорости и изменении скорости при постоянной высоте.
с минимальной затратой горючего, если задана норма расхода горючего при изменении высоты и неизменной скорости и изменении скорости при постоянной высоте. на 5 равных частей, а интервал высот на 4. Затраты топлива
на 5 равных частей, а интервал высот на 4. Затраты топлива  заданы и записаны у ребер полученного графа.
заданы и записаны у ребер полученного графа. , а также минимальными затратами топлива
, а также минимальными затратами топлива  , необходимыми для перевода самолета из текущего в конечное состояние, управляющее воздействие заключается в выборе состояния, в которое необходимо перевести самолет в следующий момент времени. Будем решать задачу методом динамического программирования – оптимизировать переход в новое состояние, начиная с последнего. Очевидно, что
, необходимыми для перевода самолета из текущего в конечное состояние, управляющее воздействие заключается в выборе состояния, в которое необходимо перевести самолет в следующий момент времени. Будем решать задачу методом динамического программирования – оптимизировать переход в новое состояние, начиная с последнего. Очевидно, что  ,
,  ,
, 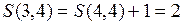 , …,
, …,  ,
,  , т.е. чтобы попасть из состояния (4,3) в конечное состояние (5,4) необходимо 2 ед. топлива. Далее
, т.е. чтобы попасть из состояния (4,3) в конечное состояние (5,4) необходимо 2 ед. топлива. Далее  .
.

 14 – минимальные затраты топлива для перехода из
14 – минимальные затраты топлива для перехода из  в
в  , очевидно, что следующим должен быть переход в состояние (0,1), т.к.
, очевидно, что следующим должен быть переход в состояние (0,1), т.к.  . Далее возможен любой переход, т.к. затраты топлива одинаковы и для перехода в (0,2) и в состояние (1,1):
. Далее возможен любой переход, т.к. затраты топлива одинаковы и для перехода в (0,2) и в состояние (1,1): 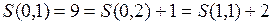 . Выберем, например, переход в (1,1). Т.о. получаем следующий режим перевода системы в конечное состояние:
. Выберем, например, переход в (1,1). Т.о. получаем следующий режим перевода системы в конечное состояние:
 функции
функции  в точках
в точках  , получена статистика
, получена статистика функции, измерения которой были получены.
функции, измерения которой были получены.
 (1)
(1) (2)
(2) (3)
(3) ,
,  ,
,  ,
,  .
. (4)
(4) ,
,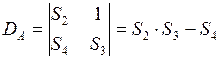 ,
, 
 (5)
(5)



 ,
,  ,
, ,
, 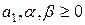 .
. - выпуск (шт.), К – основные фонды (тыс.руб.), L – трудовые ресурсы
- выпуск (шт.), К – основные фонды (тыс.руб.), L – трудовые ресурсы 


