
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок листових конструкційСодержание книги
Поиск на нашем сайте Розрахунок на міцність
1.10.1.1 Розрахунок на міцність листових конструкцій (оболонок обертання), які перебувають у безмоментному напруженому стані, слід виконувати за формулою
де x і y – нормальні напруження у двох взаємно перпендикулярних напрямках; с – коефіцієнт умов роботи конструкцій, який призначається згідно з табл. 1.1.1 цих норм. При цьому абсолютні значення головних напружень повинні бути не більшими за значення розрахункових опорів, помножених на с.
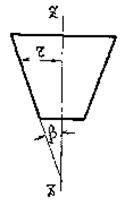
1.10.1.2 Напруження у безмоментних тонкостінних оболонках обертання (рис. 1.10.1), які перебувають під тиском рідини, газу або сипучого матеріалу, слід визначати за формулами:
де 1 і 2 – відповідно меридіальне і кільцеве напруження; F – проекція на вісь z – z оболонки повного розрахункового тиску, що діє на частину оболонки abc (рис. 1.10.1); r, – радіус і кут, показані на рис. 1.10.1; t – товщина оболонки; – розрахунковий тиск на одиницю поверхні оболонки; r 1, r 2 – радіуси кривизни у головних напрямках середньої поверхні оболонки.
1.10.1.3 Напруження у стиснутих безмоментних тонкостінних оболонках обертання, що перебувають під внутрішнім рівномірним тиском, слід визначити за формулами: – для циліндричних:
- для сферичних:
- для конічних:
де – розрахунковий внутрішній тиск на одиницю поверхні оболонки; r – радіус середньої поверхні оболонки; – кут між твірною конуса і його віссю z – z (рис. 1.10.1).
1.10.1.4 При перевірці міцності оболонок у місцях зміни їхньої форми чи товщини, а також зміни навантаження слід враховувати місцеві напруження (крайових ефект).
Розрахунок на стійкість
1.10.2.1 Розрахунок на стійкість замкнутих кругових циліндричних оболонок обертання, рівномірно стиснутих у паралельному до твірної напрямку, слід виконувати за формулою
де 1 – розрахункове напруження в оболонці; cr, 1 – критичне напруження, що дорівнює: – при – при тут r – радіус серединної поверхні оболонки; t – товщина оболонки. Значення коефіцієнтів при
Значення коефіцієнту c слід визначати за табл. 1.10.1. Таблиця 1.10.1 Коефіцієнти с для розрахунку оболонок на стійкість
У випадку позацентрового стиску у паралельному до твірної напрямку або в разі чистого згину в діаметральній площині при значеннях дотичних напруженнях у розрахунковому перерізі, де діє найбільший згинальний момент, що не перевищують значення 0,07 Е (t / r)3/2, напруження cr, 1 повинно бути збільшене в (1,1 – 0,1
1.10.2.2 У трубах, що розраховуються як стиснуті або позацентрово стиснуті стрижні при умовній гнучкості
Такі труби слід розраховувати на стійкість згідно з вимогами розділів 1.4 і 1.6 незалежно від розрахунку на стійкість їх стінок. У випадку, якщо
1.10.2.3 Циліндрична панель, обперта вздовж двох твірних і двох дугах напрямної, рівномірно стиснута вдовж твірних, при - при розрахунковому напруженні Ј 0,8 Ry:
- при розрахунковому напруженні = Ry:
При Якщо
1.10.2.4 Розрахунок на стійкість замкнутої кругової циліндричної оболонки обертання при дії зовнішнього рівномірного тиску , спрямованого нормально до бічної поверхні, слід виконувати за формулою
де cr, 2 – критичне напруження, що визначається за формулами: – при
- при
де l – довжина циліндричної оболонки. При 10 < l / r < 20 напруження cr, 2 слід визначати за лінійною інтерполяцією. Та ж сама оболонки, але підкріплена кільцевими ребрами жорсткості, розміщеними з кроком s і 0,5 r між осями ребер, повинна бути розрахована на стійкість за формулами (1.10.12) – (1.10.14) із заміною в них значення l на значення s. У цьому випадку повинна задовольнятися перевірка загальної стійкості ребра у своїй площині, виконана як для центрально стиснутого стрижня відповідно до вимог п. 1.4.1.3 на дію поздовжнього зусилля N = rs при розрахунковій довжині стрижня lef = 1,8 r; при цьому у розрахунковий переріз ребра жорсткості слід включати ділянки оболонки завширшки При використанні одностороннього ребра жорсткості його момент інерції слід обчислювати відносно осі, що збігається з найближчою поверхнею оболонки.
1.10.2.5 Розрахунок на стійкість замкнутої кругової циліндричної оболонки обертання, яка підлягає одночасній дії зусиль, зазначених у п. 1.10.2.1 і п. 1.10.2.4, слід виконувати за формулою
де cr, 1 обчислюють згідно з вимогами п. 1.10.2.1, а cr , 2 – відповідно до вимог п. 1.10.2.4.
1.10.2.6 Розрахунок на стійкість конічної оболонки обертання з кутом конусності Ј 60°, стиснутої поздовжньою силою N вдовж осі (рис. 1.10.3), слід виконувати за формулою
де Ncr – критична сила, що визначається за формулою
тут t – товщина оболонки; cr, 1 – значення критичного напруження, обчислене згідно з вимогами п. 1.10.2.1, із заміною радіуса r на радіус rm, що дорівнює
1.10.2.7 Розрахунок на стійкість конічної оболонки обертання при дії зовнішнього рівномірного тиску , спрямованого нормально до бічної поверхні, слід виконувати за формулою
тут 2 = rm / t – розрахункове кільцеве напруження в оболонці; cr ,2 – критичне напруження, що визначається за формулою
де rm – радіус, що визначається за формулою (1.10.18); h – висота конічної оболонки (між основами).
1.10.2.8 Розрахунок на стійкість конічної оболонки обертання, що підлягає одночасній дії навантажень, зазначених в п. 1.10.2.6 і п. 1.10.2.7, слід виконувати за формулою
де значення Ncr і cr, 2 слід обчислювати за формулами (1.10.17) і (1.10.20) відповідно.
1.10.2.9 Розрахунок на стійкість повної сферичної оболонки (чи її сегмента) при r / t Ј 750і дії зовнішнього рівномірного тиску , спрямованого нормально до її поверхні, слід виконувати за формулою
де
тут r – радіус серединної поверхні сферичної оболонки.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , (1.10.1)
, (1.10.1) ; (1.10.2)
; (1.10.2) , (1.10.3)
, (1.10.3)

 ;
;  ; (1.10.4)
; (1.10.4) ; (1.10.5)
; (1.10.5)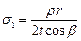 ;
;  , (1.10.6)
, (1.10.6) , (1.10.7)
, (1.10.7) – меншому із значень Ry чи cEt / r;
– меншому із значень Ry чи cEt / r; –
–  ;
; слід визначити за формулою
слід визначити за формулою . (1.10.8)
. (1.10.8)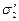 / 1) разів, де
/ 1) разів, де  0,65 повинна бути виконана умова
0,65 повинна бути виконана умова . (1.10.9)
. (1.10.9) , то розрахунок на стійкість стінок безшовних чи електрозварних труб не потрібен.
, то розрахунок на стійкість стінок безшовних чи електрозварних труб не потрібен.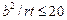 (де b – ширина панелі, виміряна вздовж дуги напрямної) повинна бути розрахована на стійкість як пластинка за формулами:
(де b – ширина панелі, виміряна вздовж дуги напрямної) повинна бути розрахована на стійкість як пластинка за формулами: ; (1.10.10)
; (1.10.10) . (1.10.11)
. (1.10.11) найбільше відношення
найбільше відношення  слід визначати лінійною інтерполяцією.
слід визначати лінійною інтерполяцією.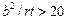 , то панель слід розраховувати на стійкість як оболонку відповідно до вимог п.п. 1.10.2.9.
, то панель слід розраховувати на стійкість як оболонку відповідно до вимог п.п. 1.10.2.9. , (1.10.12)
, (1.10.12) – розрахункове кільцеве напруження в оболонці;
– розрахункове кільцеве напруження в оболонці; :
: , (1.10.13)
, (1.10.13) :
: , (1.10.14)
, (1.10.14) з кожного боку від осі ребра, а умовна гнучкість стрижня
з кожного боку від осі ребра, а умовна гнучкість стрижня 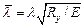 не повинна перевищувати 6,5.
не повинна перевищувати 6,5. , (1.10.15)
, (1.10.15) (1.10.16)
(1.10.16) (1.10.17)
(1.10.17) . (1.10.18)
. (1.10.18) , (1.10.20)
, (1.10.20)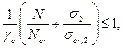 (1.10.21)
(1.10.21) , (1.10.22)
, (1.10.22) – розрахункове напруження;
– розрахункове напруження; – критичне напруження, що приймається не більшим за значення Ry;
– критичне напруження, що приймається не більшим за значення Ry;


