
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет размерных цепей методом максимума-минимумаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Метод расчета учитывает только предельные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания (например, все увеличивающие звенья имеют наибольшие предельные размеры, а все уменьшающие – наименьшие предельные размеры или наоборот). 5.1.1. Прямая задача может решаться двумя способами: способом назначения равных допусков или назначения допусков одного квалитета. Способ назначения равных допусков применяют в случаях, когда номинальные размеры составляющих звеньев входят в один интервал размеров и могут быть выполнены с одинаковой точностью. Допуск каждого составляющего звена в этом случае равен
где Полученный допуск
т.е. сумма допусков составляющих звеньев должна быть равна допуску исходного звена. При корректировке стремятся использовать стандартные поля допусков по ГОСТ 25347-82. Способ равных допусков находит ограниченное применение, поскольку сравнительно редко встречаются размерные цепи, составляющие звенья которых входили бы в один интервал размеров. Обычно этот способ используют для быстрой предварительной оценки среднего значения искомых допусков в целях установления их приемлемости и последующей корректировки. Способ назначения допусков одного квалитета исходит из условия, что составляющие звенья выполнены по какому-либо одному квалитету. В этом случае расчетное число единиц допуска, одинаковое для всех составляющих звеньев,
где Примечание. При решении по формулам (5.2) и (5.4) из числа составляющих звеньев цепи исключают размеры покупных деталей и сборочных единиц, точность которых уже установлена стандартами (например, размеры подшипников качения). Сравнивая полученное расчетное значение
По заданным предельным значениям исходного звена
где
Для увеличивающих звеньев предельные отклонения рекомендуется назначать как для основных отверстий, принимая Примечание. Если предельные отклонения исходного звена симметричны относительно его номинального размера, т.е. равны Сущность решения прямой задачи методом максимума-минимума рассмотрим на следующем примере. Пример. Определить допуски и предельные отклонения составляющих звеньев размерной цепи узла, представленного на рис. 5.1 ( Ввиду значительного различия составляющих звеньев цепи решение задачи способом назначения равных допусков нецелесообразно. Применяем способ назначения допусков одного квалитета. Порядок расчета 5.1.1.1. Пользуясь рис. 5.1, выявляем увеличивающие ( 5.1.1.2. По формуле (5.1) определяем номинальный размер исходного звена: 5.1.1.3. На основании зависимостей (5.5) и (5.6) находим предельные отклонения исходного звена:
Таким образом, исходное звено 5.1.1.4. Из табл. П.6 выписываем значения единицы допуска для интервалов, соответствующих номинальным размерам звеньев 5.1.1.5. По формуле (6.4) определяем расчетное число единиц допуска:
5.1.1.6. Сравнивая полученное значение 5.1.1.7. Пользуясь формулой (5.3), находим, что
5.1.1.8. Назначаем предельные отклонения составляющих звеньев размерной цепи:
5.1.1.9. На основании формул (5.7) и (5.8) получаем, что
Следовательно, предельные отклонения составляющих звеньев выбраны правильно. 5.1.2. Обратная задача. Сущность её решения методом максимума-минимума рассмотрим на следующем примере. Пример. Определить номинальный размер, допуск и предельные отклонения замыкающего звена (зазора) размерной цепи узла, представленного на рис. 5.3 ( Порядок расчета 5.1.2.1. Пользуясь рис. 5.3, выявляем увеличивающие ( 5.1.2.2. По формуле (5.1) определяем номинальный размер замыкающего звена:
5.1.2.3. По табл. 7 и 8 ГОСТ 25347-82 находим предельные отклонения составляющих звеньев:
5.1.2.4. На основании формул (5.7) и (5.8) устанавливаем предельные отклонения и допуск замыкающего звена:
5.1.2.5. По формуле (5.3) получаем, что
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 1737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.142.94 (0.009 с.) |

 (5.2)
(5.2)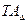 – допуск исходного звена, мкм.
– допуск исходного звена, мкм.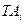 корректируют для отдельных составляющих звеньев в зависимости от их значений, конструктивных и технологических требований так, чтобы удовлетворялось уравнение
корректируют для отдельных составляющих звеньев в зависимости от их значений, конструктивных и технологических требований так, чтобы удовлетворялось уравнение (5.3)
(5.3) (5.4)
(5.4)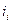 – единица допуска i- того составляющего звена, определяемая по табл. П.6, мкм;
– единица допуска i- того составляющего звена, определяемая по табл. П.6, мкм; 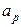 с ближайшим в табл. П.7 табличным значением
с ближайшим в табл. П.7 табличным значением 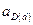 , устанавливают квалитет и по табл. 6 ГОСТ 25346-89 назначают допуски составляющих звеньев. В общем случае
, устанавливают квалитет и по табл. 6 ГОСТ 25346-89 назначают допуски составляющих звеньев. В общем случае  и
и  находят его верхнее и нижнее предельные отклонения:
находят его верхнее и нижнее предельные отклонения: (5.5)
(5.5) (5.6)
(5.6)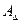 – номинальный размер исходного звена, определяемый по формуле (5.1), мм. С учетом принятых допусков назначают предельные отклонения
– номинальный размер исходного звена, определяемый по формуле (5.1), мм. С учетом принятых допусков назначают предельные отклонения 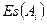 и
и 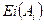 составляющих размеров так, чтобы выполнялись условия:
составляющих размеров так, чтобы выполнялись условия: , (5.7)
, (5.7) . (5.8)
. (5.8) и
и  , а для уменьшающих звеньев – как для основных валов, принимая
, а для уменьшающих звеньев – как для основных валов, принимая  и
и 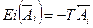 .
. , то предельные отклонения составляющих звеньев рекомендуется также выбирать равными
, то предельные отклонения составляющих звеньев рекомендуется также выбирать равными  .
.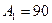 мм,
мм, 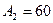 мм,
мм,  мм,
мм,  мм,
мм, 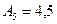 мм), если предельные значения исходного звена (зазора) равны
мм), если предельные значения исходного звена (зазора) равны 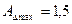 мм и
мм и  мм.
мм.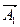 ,
, 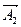 ) и уменьшающие (
) и уменьшающие (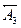 ,
, 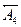 ,
, 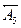 ) звенья, строим схему размерной цепи (рис. 5.2).
) звенья, строим схему размерной цепи (рис. 5.2).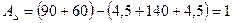 мм.
мм.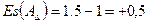 мм,
мм,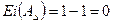 .
.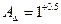 мм, а его допуск
мм, а его допуск 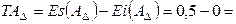 = 0,5 мм = 500 мкм.
= 0,5 мм = 500 мкм.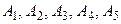 :
: 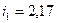 мкм,
мкм, 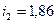 мкм,
мкм, 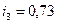 мкм,
мкм, 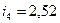 мкм,
мкм, 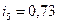 мкм.
мкм.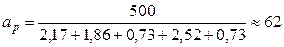 .
.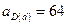 , устанавливаем квалитет 10 и по табл. 6 ГОСТ 25346-89 назначаем допуски составляющих звеньев:
, устанавливаем квалитет 10 и по табл. 6 ГОСТ 25346-89 назначаем допуски составляющих звеньев: 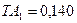 мм,
мм, 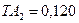 мм,
мм, 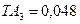 мм,
мм, 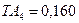 мм,
мм, 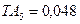 мм.
мм.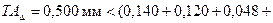
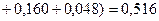 мм, и поэтому допуск одного или сумму допусков нескольких составляющих звеньев необходимо уменьшить на 0,016 мм. Выбираем для этого звенья
мм, и поэтому допуск одного или сумму допусков нескольких составляющих звеньев необходимо уменьшить на 0,016 мм. Выбираем для этого звенья 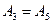 , которые легко обработать с более высокой точностью, и вместо допусков
, которые легко обработать с более высокой точностью, и вместо допусков 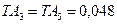 мм устанавливаем для них допуски
мм устанавливаем для них допуски 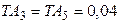 мм, т.е. уменьшаем в сумме на 0,016 мм.
мм, т.е. уменьшаем в сумме на 0,016 мм.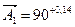 мм,
мм, 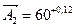 мм,
мм, 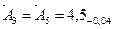 мм,
мм, 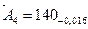 мм.
мм.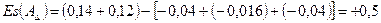 мм,
мм,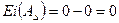 .
.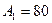 мм,
мм, 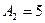 мм,
мм, 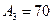 мм и
мм и 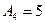 мм), если для увеличивающих звеньев установлены поля допусков F8, а для уменьшающих – d9.
мм), если для увеличивающих звеньев установлены поля допусков F8, а для уменьшающих – d9.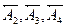 ) звенья, строим схему размерной цепи (рис. 5.4).
) звенья, строим схему размерной цепи (рис. 5.4).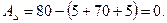
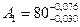 мм,
мм, 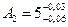 мм,
мм, 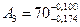 мм,
мм, 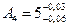 мм.
мм.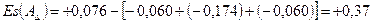 мм,
мм,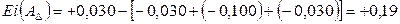 мм,
мм,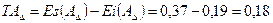 мм.
мм.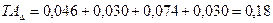 мм, следовательно, задача решена правильно:
мм, следовательно, задача решена правильно: 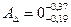 мм.
мм.


