Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стрілець робить 3 постріла. Знайти число потраплень в ціль при трьох вистрілах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На базе 10 автомашин. Чтоб не меньше 8 вышло. Найти вероятность нормальной работы. Так как n-мало, то нужно применить формулу Бернулли:
Р10(8)= Р10(9)= Р10(10)=
При даному технологічному процесі 80% всієї виготовленої продукції являється продукцією найвищого ґатунку. Яким повинен бути об’єм вибірки, щоб з ймовірністю 0,95 відхилення фактичної частоти m/n від ймовірності 0,8 було не менше чім 4%. Рішення:
Найдем n: Ответ:400
В пачке 20 карт (от 100 до 120) и произвольно расположены. Извлекают 2 карты. Найти вероятность того, что будут извлечены карты с номерами 101 и 120. Решим по классическому определению вероятности:
Монета брошена 2 раза. Найти вероятность того, что хотя бы 1 раз появится герб. Решим по классическому определению вероятности:
Общее число исходов опыта n=4, так как может выпасть: Герб Решка Решка Герб Решка Решка Герб Герб Число благоприятных исходов m=3, так как встречается герб в 3 парах. Ответ: 3/4. В коробке 6 одинаковых занумерованных кубиков. По одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке. Решим по классическому определению вероятности:
Общее число исходов опыта n=6! – число перестановок 6 кубиков по 6 местам.Число благоприятных исходов m=1 – (1,2,3,4,5,6). Ответ: 1/720.
В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вер-ть того, что среди извлеченных деталей: а) нет бракованных; б) нет годных. Решение. Т.к. порядок извлечения деталей не важен, используем формулу для сочетаний С m эл-тов из n данных. По классическому определению вер-ти: а) В партии из N деталей имеется nстандартных. Наудачу отобраны m деталей. Найти вер-ть того, что среди отобранных ровно k стандартных. Решение. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти Р того, что среди 5 взятых наудачу кинескопов окажется 3 львовских. Решение. Воспользуемся формулой:
N=15; n=10; k=3; m=5.
В группе 12 студентов, из которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вер-ть того, что среди отобранных студентов 5 отличников. Решение. Воспользуемся формулой:
Задумано двузначное число, цифры которого различны. Найти Р того, что задуманным числом окажется: а) случайно названное двузначное число; б) двузначное число, цифры которого различны. Решение. а) Р=1/90; б) Р=1/81. В конверте среди 100 фотокарточек находится 1 разыскиваемая. Из конверта наудачу извлекли 10 карточек. Найти Р того, что среди них окажется нужная. Решение. Т.к. порядок извлечения деталей не важен, используем формулу для сочетаний С m эл-тов из n данных. По классическому определению вер-ти:
Устройство состоит из 5 элементов, из которых 2 изношены. При включении устройства включаются случайным образом 2 эл-та. Найти Р того, что включенными окажутся неизношенные Эл-ты. Решение. Т.к. порядок извлечения деталей не важен, используем формулу для сочетаний С m эл-тов из n данных. По классическому определению вер-ти:
Набирая номер телефона, абонент забыл последние 3 цифры, но помня лишь то, что те цифры различны, набрал их наугад. Найти вер-ть того, что набраны нужные цифры. Решение. Т.к. порядок извлечения деталей важен, используем формулу для размещений А m эл-тов из n данных. Благоприятный исход m=1.
В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти Р того, что среди 2 извлеченных изделий окажутся: а) одно окрашенное; б) 2 окрашенных; в) хотя бы одно окрашенное. а) Пусть событие А-1 из изделий окрашенное. В- не окрашенное изделие. Тогда А1-при 1-м вытягивании 1 окрашенное изделие. В1- при 1-м вытягивании 1 неокрашенное изделие. А1-при 2-м вытягивании 1 окрашенное изделие. В2- при 2-м вытягивании 1 неокрашенное изделие. Отсюда, Р(А)=Р(А1В2)+Р(В1А2). Р(А)= б) Событие А – 2 изделия из 2 окрашенные. Р(А)=Р(А1А2)= в) Событие А – хотя бы одно изделие окрашенное. Р(А)=Р(А1В1)+Р(А2В1)+Р(А1А2). События А и В составляют полную группу. Отсюда: Р(А)=Р( На столі в довільному порядку лежать 32 екзаменаційних білета. Чому дорівнює ймовірність того, що номер навмання взятого білету буде числом, кратним 3 або 7? Решение. В совокупности чисел от 1 до 32 содержится 4 числа, кратных 7, и 10 чисел, кратных 3.
Отсюда, Р(А)=4/32 + 10/32 = 14/32 = 7/16.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.134 (0.01 с.) |






 , де
, де 
 2Ф(х)=0,95 отсюда х=1,96
2Ф(х)=0,95 отсюда х=1,96 n= 400
n= 400
 Ответ: 1/190.
Ответ: 1/190.
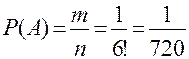
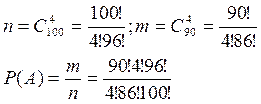 б)
б) 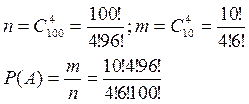


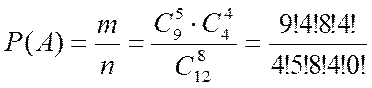
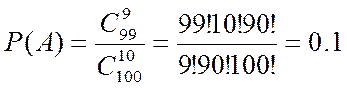
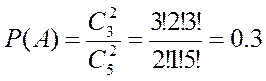
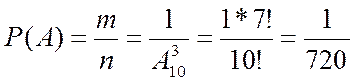


 -В1В2)=
-В1В2)=