
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вер-ть того, что среди отобранных лиц окажутся 3 женщины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вироб перевіряється на якість одним з двох товарознавців. Ймовірність того, що вироб попаде до першого товарознавця, дорівнює 0,33, до другого – 0,45. Ймовірність того, що вироб буде признано стандарним першим товарознавцем, дорівнює 0,9, другим – 0,95. Вироб при перевірці було признано стандартним. Знайти ймовірність того, що вироб перевірив другий товарознавець. Н1={изделие попало к первому товароведу} Н2={изделие попало ко второму товароведу} Р(Н1)=0,33; Р(Н2)=0,45. А= {изделие признано стандартным} РН1(А)=Р(изделие признано стандартным первым товароведом)=0,9 РН2(А)=Р(изделие признано стандартным вторым товароведом)=0,95 По формуле Байеса:
Р(А)=0,33*0,9+0,45*0,95=0,297+0,427=0,724 РА(Н2)=0,45*0,95/0,724=0,591 Значит, вероятность того, что изделие проверил второй товаровед равна 59,1%.
Середня кількість замовлень на таксі, що надходить на диспетчерський пункт за 1 хвилину, дорівнює 4. Знайти ймовірність того, що за 2 хвилини надійде: а) 5 викликів; б) менше 4 викликів. Решение. Задачу решаем с помощью формулы Пуассона.
а) Рn(5)= б) Рn(x<4)=Pn(3)+ Pn(2)+ Pn(1)+ Pn(0) Воспользуемся формулой:
Рn(0)= Рn(1)= Рn(2)= Рn(3)= Рn(x<4)=0,195367+0,146525+0,073263+0,018316=0,433471 Відомо, що 4% чоловіків і 21% жінок дальтоніки. А – навмання взята людина - дальтонік. Знайти ймовірність того, що це буде чоловік. Розв’язок: Будем использовать формулу Байеса Н1 – наугад взятый человек – мужчина Н2 – наугад взятый человек – женщина Р(Ні)=1/2 и составляет полную группу. Выдвинутые события образуют группу событий, т.к. наугад взятый человек может быть либо мужчина либо женщина.
Ответ:0,16 Завод випускає 80% продукції вищої якості. В вибірку взято 200 одиниць. Яке найвірогідніше число виробів вищої якості? Яка ймовірність найвірогіднішого числа? Яка ймовірність того, що продукції вищої якості не менше 150 одиниць? Розв’язок: Найдем наивероятнейшее число изделий высшего качества m0
200*0.8-0.2< m0<200*0.8+0.8 159.8< m0<160.8, отсюда m0=160 Вероятность наивероятнейшего числа:
А – выпущенная продукция высшего качества. Если вероятность р появления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно большое, то вероятность того, что в этих испытаниях соб. А произойдет не менее m1 и не более m2 раз, как и в нашей задаче, то надо использовать формулу Лапласа:
Т.к. Ответ:1 Випадкова величина розподілена за законом Пуассона з параметром Решение. а) Р(m>5) = 1- Р(5)- Р(4)- Р(3)- Р(2)- Р(1)- Р(0). Воспользуемся формулой Пуассона: Рn(0)= Рn(3)= Р(m>5)=1- (е-1+ е-1+ 2е-1+ 6е-1+ 24е-1 + 120е-1) б) P(m=4)=Р(4)= 24е-1; в) P(10<m<=13)= Р(11)+ Р(12)+ Р(13) Рn(11)= Три студенти йдуть на іспит. Імовірність того, що перший студент складе іспит, дорівнює 0,6; для другого – 0,7; для третього – 0,75. Знайти імовірність того, що хоча б один студент складе іспит. Решение. Пусть А1, А2 и А3 – события, которые состоят в том, что экзамен будет сдан соответственно первым, вторым и третим студентом. А событие А том, что экзамен сдаст хотя бы один студент. По условию задачи известно, что р1=0,6; р2=0,7 и р3=0,75. Тогда q1=0,4;q2=0,3;q3=0,25. Итак, вероятность того, что хотя бы один студент сдаст экзамен, равна: Р(А)=Р(А1+А2+А3)=1-0,4*0,3*0,25=0,97 Пусть нужно найти вер-ть того, что хотя бы два студента сдадут экзамен. Распишем событие А через элементарные:
В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вер-ть того, что среди отобранных лиц окажутся 3 женщины. Решение. Интересующее нас событие А состоит в том, что среди отобранных 7 человек 3 женщины.
Для каждой тройки женщин (m=4) можно выбрать С46 четверок мужчин:
Стрілець робить 3 постріла. Знайти число потраплень в ціль при трьох вистрілах.
На базе 10 автомашин. Чтоб не меньше 8 вышло. Найти вероятность нормальной работы. Так как n-мало, то нужно применить формулу Бернулли:
Р10(8)= Р10(9)= Р10(10)=
При даному технологічному процесі 80% всієї виготовленої продукції являється продукцією найвищого ґатунку. Яким повинен бути об’єм вибірки, щоб з ймовірністю 0,95 відхилення фактичної частоти m/n від ймовірності 0,8 було не менше чім 4%. Рішення:
Найдем n: Ответ:400
В пачке 20 карт (от 100 до 120) и произвольно расположены. Извлекают 2 карты. Найти вероятность того, что будут извлечены карты с номерами 101 и 120. Решим по классическому определению вероятности:
Вироб перевіряється на якість одним з двох товарознавців. Ймовірність того, що вироб попаде до першого товарознавця, дорівнює 0,33, до другого – 0,45. Ймовірність того, що вироб буде признано стандарним першим товарознавцем, дорівнює 0,9, другим – 0,95. Вироб при перевірці було признано стандартним. Знайти ймовірність того, що вироб перевірив другий товарознавець. Н1={изделие попало к первому товароведу} Н2={изделие попало ко второму товароведу} Р(Н1)=0,33; Р(Н2)=0,45. А= {изделие признано стандартным} РН1(А)=Р(изделие признано стандартным первым товароведом)=0,9 РН2(А)=Р(изделие признано стандартным вторым товароведом)=0,95 По формуле Байеса:
Р(А)=0,33*0,9+0,45*0,95=0,297+0,427=0,724 РА(Н2)=0,45*0,95/0,724=0,591 Значит, вероятность того, что изделие проверил второй товаровед равна 59,1%.
Середня кількість замовлень на таксі, що надходить на диспетчерський пункт за 1 хвилину, дорівнює 4. Знайти ймовірність того, що за 2 хвилини надійде: а) 5 викликів; б) менше 4 викликів. Решение. Задачу решаем с помощью формулы Пуассона.
а) Рn(5)= б) Рn(x<4)=Pn(3)+ Pn(2)+ Pn(1)+ Pn(0) Воспользуемся формулой:
Рn(0)= Рn(1)= Рn(2)= Рn(3)= Рn(x<4)=0,195367+0,146525+0,073263+0,018316=0,433471 Відомо, що 4% чоловіків і 21% жінок дальтоніки. А – навмання взята людина - дальтонік. Знайти ймовірність того, що це буде чоловік. Розв’язок: Будем использовать формулу Байеса Н1 – наугад взятый человек – мужчина Н2 – наугад взятый человек – женщина Р(Ні)=1/2 и составляет полную группу. Выдвинутые события образуют группу событий, т.к. наугад взятый человек может быть либо мужчина либо женщина.
Ответ:0,16 Завод випускає 80% продукції вищої якості. В вибірку взято 200 одиниць. Яке найвірогідніше число виробів вищої якості? Яка ймовірність найвірогіднішого числа? Яка ймовірність того, що продукції вищої якості не менше 150 одиниць? Розв’язок: Найдем наивероятнейшее число изделий высшего качества m0
200*0.8-0.2< m0<200*0.8+0.8 159.8< m0<160.8, отсюда m0=160 Вероятность наивероятнейшего числа:
А – выпущенная продукция высшего качества. Если вероятность р появления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно большое, то вероятность того, что в этих испытаниях соб. А произойдет не менее m1 и не более m2 раз, как и в нашей задаче, то надо использовать формулу Лапласа:
Т.к. Ответ:1 Випадкова величина розподілена за законом Пуассона з параметром Решение. а) Р(m>5) = 1- Р(5)- Р(4)- Р(3)- Р(2)- Р(1)- Р(0). Воспользуемся формулой Пуассона: Рn(0)= Рn(3)= Р(m>5)=1- (е-1+ е-1+ 2е-1+ 6е-1+ 24е-1 + 120е-1) б) P(m=4)=Р(4)= 24е-1; в) P(10<m<=13)= Р(11)+ Р(12)+ Р(13) Рn(11)= Три студенти йдуть на іспит. Імовірність того, що перший студент складе іспит, дорівнює 0,6; для другого – 0,7; для третього – 0,75. Знайти імовірність того, що хоча б один студент складе іспит. Решение. Пусть А1, А2 и А3 – события, которые состоят в том, что экзамен будет сдан соответственно первым, вторым и третим студентом. А событие А том, что экзамен сдаст хотя бы один студент. По условию задачи известно, что р1=0,6; р2=0,7 и р3=0,75. Тогда q1=0,4;q2=0,3;q3=0,25. Итак, вероятность того, что хотя бы один студент сдаст экзамен, равна: Р(А)=Р(А1+А2+А3)=1-0,4*0,3*0,25=0,97 Пусть нужно найти вер-ть того, что хотя бы два студента сдадут экзамен. Распишем событие А через элементарные:
В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вер-ть того, что среди отобранных лиц окажутся 3 женщины. Решение. Интересующее нас событие А состоит в том, что среди отобранных 7 человек 3 женщины.
Для каждой тройки женщин (m=4) можно выбрать С46 четверок мужчин:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1683; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.008 с.) |


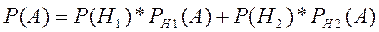
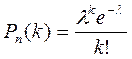 , где
, где  =np=M(x)=D(x)=4, х – число вызовов за 1 минуту.
=np=M(x)=D(x)=4, х – число вызовов за 1 минуту.
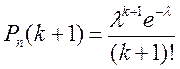







 ,
, 
 , тогда
, тогда  =0,3989
=0,3989
 , где
, где  ,
,  ,
,  - интегральная функция Лапласа
- интегральная функция Лапласа
 =1. Знати ймовірність таких подій: а) Р(m>5), б) P(m=4), в) P(10<m<=13).
=1. Знати ймовірність таких подій: а) Р(m>5), б) P(m=4), в) P(10<m<=13). .
. Рn(1)=
Рn(1)=  Рn(2)=
Рn(2)= 
 Рn(4)=
Рn(4)=  Рn(5)=
Рn(5)= 
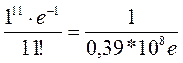 Рn(12)=
Рn(12)=  Рn(13)=
Рn(13)= 








 , де
, де 
 2Ф(х)=0,95 отсюда х=1,96
2Ф(х)=0,95 отсюда х=1,96 n= 400
n= 400
 Ответ: 1/190.
Ответ: 1/190.


