Інтегральний допплерівський рахунок

Звернемося тепер до геодезичного режиму роботи глобальних систем - фазовим вимірюванням на несучій частоті. В цьому випадку вимірюється не час розповсюдження сигналу від супутника до приймача, а зсув фази коливань несучої частоти (випромінюваної супутником) за цей час, але - і це створює головну проблему - не повний зсув j_SR, пов'язаний з відстанню від супутника S до приймача R, а лише його дробова частина, менша 2 p. Це та ж проблема вирішення неоднозначності, яка виникає і в наземних фазових віддалемірах. Зсув вимірюваних фаз реалізується в приймачі як різниця фаз між сигналом, прийнятим від супутника, і опорним сигналом, що генерується в приймачі. Припустимо, що для якогось фіксованого моменту часу ми зміряли дробову частину фазового зсуву Dj. Але, щоб визначити відстань, нам потрібен повний фазовий зсув, який дорівнює

j_SR = 2pN + Dj = wt = 2pf (P/c) (8.3)

де N - невідоме ціле число, f - несуча частота, Р - псевдодальність, що містить геометричну відстань r. З формули 8.3 легко отримати Р, враховуючи, що с/f = l (довжина хвилі у вакуумі):

Р = lN + l (Dj/2p). (8.4)

Це майже та ж псевдодальність, що і при кодових вимірюваннях, і її можна представити виразом вигляду (6.2), але з двома характерними відмінностями. По-перше, іоносферний член D_і при фазових вимірюваннях матиме інший знак (див. наступний розділ). А по-друге, величина Dt_г, яка фігурує в (6.2), матиме дещо інше трактування. При кодових вимірюваннях вона відображає несинхронність ходу годинника супутника і приймача. При фазових же вимірюваннях вона є слідством несинфазності (неспівпадання початкових фаз) коливань опорних генераторів супутника і приймача, яку ми позначатимемо через dj. Саме наявність величини dj призводить до того, що ми і з фазових вимірювань одержуємо псевдодальність. Зрозуміло Dt_г і dj жорстко пов'язані один з одним (dj = 2pf ·Dt_г), оскільки, внаслідок єдності еталона часу і частоти, “годинник” - це і є генератори коливань.

В літературі часто вживають вирази “кодова псевдодальність” і “фазова псевдодальність”. Додамо їм індекси “ к ” і “ ф ” і запишемо, з урахуванням зроблених зауважень, у вигляді:

Р_к = r + D_т + D_і + с Dt_г (8.5)

Р_ф = r + D_т - D_і + c( dj/2pf). (8.6)

Прирівнюючи (8.4) і (8.6), визначимо величину Dj/2p, позначаючи її через Ф (виміряна величина різниці фаз, виражена в частках циклу - те, що в наземній фазовій віддалеметрії позначають як DN):

Ф = (r/l) - N + (D_т/ l) - (D_и/l) + (dj/2p). (8.7)

Присутність невідомого цілого числа N приводить, як вже згадувалося, до проблеми вирішення неоднозначності.

Звичайно в літературі рівняння фазових вимірювань використовують у вигляді (8.7).

Якщо ми якимсь чином визначили число N, то можна отримати виміряне значення фазової псевдодальності Р_ф. Проте вона містить невідому величину dj. Фазові вимірювання з двома приймачами дозволяють виключити цю величину, використовуючи так званий метод фазових різниць.

Метод фазових різниць. Для виключення dj достатньо виконати вимірювання не до чотирьох, як при кодових вимірюваннях, а тільки до двох супутників. Величину dj можна представити різницею dj_S - dj_R (тобто різницею початкових фаз коливань генераторів на супутнику і в приймачі). Якщо виконати спостереження одного і того ж супутника одночасно двома приймачами, що рознесені на деяку відстань (в пункти А і В), то в різниці двох рівнянь вигляду (8.7) виключається величина dj_S для спостережуваного супутника.

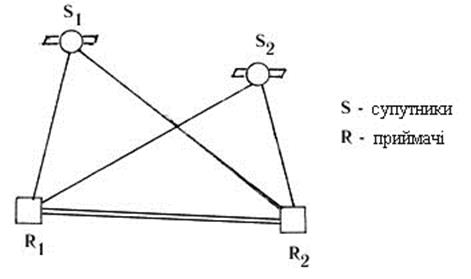
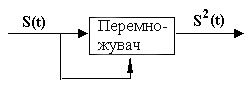
Рис.8.2. Геометрія спостережень для отримання другої фазової різниці

Якщо виконати тими ж приймачами і в ту ж епоху спостереження другого супутника, то в різниці виключається величина dj_S для цього другого супутника. Якщо тепер скласти різницю різниць - так звану другу різницю (позначимо її DФ_II), - то виключається величина dj_R для обох приймачів. Геометрія вимірювань показана на рис.8.2.

Таким чином, в другій різниці ліквідовується крупний недолік одностороннього (беззапитного) фазового методу – невідома відмінність початкових фаз коливань на супутнику і в приймачі. Тому спосіб других різниць є основним при точних геодезичних вимірюваннях.

Проте цей спосіб не ліквідовує іншого крупного недоліку фазових вимірювань - необхідності вирішення неоднозначності.

Відмітимо, що якщо повторити вищеописану процедуру спостереження двох супутників двома приймачами в інший момент часу, тобто коли ці супутники займуть інше положення, і так само отримати другу різницю, а потім скласти різницю других різниць – третю різницю (DФ_III), то неоднозначність, як часто говорять, виключається. Насправді це не так: неоднозначність в цьому випадку не виключається, а, так би мовити, ігнорується. Суть справи тут полягає в тому, що при утворенні третьої різниці в неї входять не самі відстані між супутниками і приймачами, а їх прирости за час переміщення супутників по орбіті. Відповідно в третій різниці фігурують не невідомі значення N фазових циклів, а їх прирости DN. Ці прирости можуть вимірюватися за показниками фазометричного пристрою при безперервному відстежуванні сигналу супутника. Знаходження ж цілих чисел N (по всіх відстанях), які мають порядок»10⁸ і повинні бути визначений з точністю до одиниці, є виключно складною задачею. Вважається, що неоднозначність вирішена, якщо точно визначені цілі числа No = (N_A – N_B)^S1 – (N_A – N_B)^S2, фігуруючі в других різницях. Процес визначення No називають ініціалізацією.

Існує декілька можливих способів визначення Nо. Проте в процесі спостережень оператор не може взнати, чи вирішена багатозначність - він дізнається про це тільки після так званої постобробки, здійснюваної на офісному комп'ютері, на який перекачуються всі дані, отримані під час роботи супутникового приймача.

Фазові вимірювання, як основа відносного методу. Якщо багатозначність вирішена, то другу фазову різницю DФ_II можна перевести в лінійну міру (множенням на довжину хвилі l). Це буде друга різниця фазових псевдодальностей, що містить величини r_А¹, r_В¹, r_А², r_В² - геометричні відстані від приймачів А і В до супутників 1 і 2. Позначимо вказану другу різницю фазових псевдодальностей через Р¹². Вона пов'язана з координатами двох супутників (X₁, Y₁, Z₁), (X₂, Y₂, Z₂) і приймачів (Х_А, У_А, Z_A), (X_B, Y_B, Z_B) співвідношенням:

Р¹² = [(X₁-X_A)² + (Y₁-Y_A)² + (Z₁-Z_A)²]^1/2 -

- [(X₁-X_B)² + (Y₁-Y_B)² + (Z₁-Z_B)²]^1/2 -

- [(X₂-X_A)² + (Y₂-Y_B)² + (Z₂-Z_B)²]^1/2 +

+ [(X₂-X_B)² + (Y₂-Y_B)² + (Z₂-Z_B)²]^1/2 + dD_а¹² (8.8)

де останній член є “подвійна різниця атмосферних затримок”, що відображає залишковий вплив атмосфери на трасах розповсюдження сигналів від супутників 1 і 2 до пунктів А і В.

Оскільки координати супутників відомі, то в (8.8) залишаються невідомими координати пунктів А і В. Якщо ми виконаємо на пунктах А і В відповідні спостереження (вимірювання фазових псевдодальностей Р_ф) до ЧОТИРЬОХ супутників (тобто як і у разі кодових вимірювань), то отримаємо три незалежні рівняння вигляду (8.8): для Р¹², Р¹³ і Р¹⁴, в котрих в якості невідомих виступатимуть три РІЗНИЦІ однойменних координат пунктів А і В - кінцевих точок базової лінії: (X_A-X_B), (Y_A-Y_B) і (Z_A-Z_B), які і визначаються з рішення системи рівнянь_. Якщо один з приймачів помістити в пункті з відомими координатами (що звичайно і роблять), то за отриманими різницями легко знаходяться координати другого пункту.

По різницях координат можна обчислити і відстань між приймачами (довжину бази):

АВ = [(X_A-X_B)² + (Y_A-Y_B)² + (Z_A-Z_B)²]^1/2. (8.9)

Точність фазових вимірювань істотно перевершує точність кодових вимірювань і складає в середньому [(5-10) + (1-2) D ] мм, де D - довжина бази в кілометрах. По висоті точність виходить дещо менше ніж в плані.

Відновлення несучої частоти при фазових вимірюваннях. В підрозділі “Кодові вимірювання” ми згадували, що зняття кодової модуляції можливо, якщо в приймачі виробляється копія такого ж коду, яким модулюється супутниковий сигнал. Але і за відсутності копії (наприклад, несуча L2 модулюється тільки Р -кодом, якого може не бути в приймачі) задача відновлення несучої розв'язується достатньо просто. Для цього використовують квадратування сигналу, що приходить від супутника. Ідея способу пояснюється на рис.8.3. Кодований сигнал від супутника розділяється на дві частини, що поступають на два входи перемножуючого пристрою. На виході утворюється сигнал, помножений сам на себе, тобто зведений в квадрат.

Рис.8.3. До способу квадратування сигналу

 

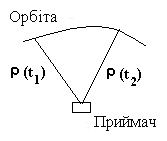
Нехай сигнал, що проходить з несучою частотою f, має вигляд:

S(t)= А cos (2pf t + j_м) (8.10)

де - індекс “ м ” при початковій фазі j означає маніпуляцію на 180^о при зміні символів коду. Використовуючи відоме співвідношення cos²a = (1/2)(1+cos2a), для вихідного сигналу знайдемо:

S²(t)= A²cos²(2pf t + j_м) = (А²/2) + (А²/2)cos(2p2f t + 2j_м). (8.11)

Множення фази j_м на 2 знімає фазову маніпуляцію, оскільки перекидання на 180^о перетворюється на зміну на 360^о, і на виході одержуємо сигнал, що складається з постійної складової (А²/2) і немодульованої несучої з амплітудою (А²/2) і подвоєною частотою 2f, яку легко можна перетворити в зручне для фазових вимірювань значення.

Інтегральний допплерівський рахунок. Під цим розуміється рахунок періодів допплерівського зсуву частоти Df_д, виникаючого через рух супутника, за деякий проміжок часу Dt = t₂ - t₁, де t₁ і t₂ - моменти початку і кінця вимірювання. Наприклад, можна таким чином підрахувати прирости фазових циклів при переміщенні супутника по орбіті з однієї точки в іншу, а значить, визначити і приріст відстані від приймача. Це дає можливість фіксувати положення супутника в різні епохи (що нагадує метод третіх різниць при фазових вимірюваннях), або, іншими словами, фіксувати послідовні зміни відстані від наземного приймача до супутника. А це, у свою чергу, означає, що можуть бути визначені відповідні різниці відстаней, що дозволяють обчислити положення приймача гіперболічною засічкою (див. розділ 6, підрозділ «Геометричні принципи позиціонування»).

Чому рахунок називається інтегральним? В приймачі частота f_пр, що приходить = f + Df_д змішується з частотою f_o опорного генератора, як правило, дещо відмінної від частоти f випромінюваних супутником коливань, і різниця частот (f_o - f_пр), яка називають частотою биття, що виділяється, інтегрується за часом на інтервалі (t₂ - t₁). Можна показати, що в результаті інтеграції визначається різниця відстаней від приймача до двох положень супутника, відповідних моментам t₁ і t₂ (рис.8.4). Фактично тут відбувається те ж, що і при інтеграції допплерівського зсуву в лазерних інтерферометрах при переміщенні відбивача, яке визначається як різниця двох положень відбивача в початковий і кінцевий моменти його руху (див. розділ 5).

За допплерівським зсувом можна знайти і швидкість зміни відстані між супутником і приймачем (див. розділ 2).

 

Рис.8.4. До допплерівського підрахунку фазових циклів при русі супутника

ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ

1. До чого відносяться фазові виміри?

2. Що являється виміряною величиною при фазових вимірах?

3. Що являється основною проблемою при фазових вимірах?

4. В чому відмінність фазової псевдодальності від кодової псевдодальності?

5. Що виключається в другій фазовій різниці?

6. При вирішенні яких рівнянь отримують остаточні значення різниць координат двох пунктів при фазових вимірах?

7. Фазові виміри виконуються на несучій частоті. Що необхідно для зняття кодової модуляції з ціллю відновлення несучої?

8. Що виключає перша, друга, третя фазові різниці на початковій фазі?

9. Супутник рухається по майже правильному колу, в центрі якого знаходиться приймач. При переміщенні супутника з точки орбіти А в точку В відстань до приймача збільшилась на 2,64 м. Чому дорівнює приріст фазових циклів на частоті L1?

10. Що дозволяє визначити число періодів при інтегральному допплерівському рахунку?