Перетворення гармонійних коливань

Модуляція. Модуляцією називається зміна параметрів коливання в часі за певним законом. Відповідно до того, який параметр модулюється (А, w або j_о), розрізняють амплітудну модуляцію (АМ), частотну (ЧМ) і фазову (ФМ). В світловіддалемірах іноді використовують ще один вид модуляції – поляризаційну (ПМ), при якій змінюється стан поляризації світлових коливань. Коливання, параметр якого модулюється, називається несучим коливанням, а його частота f = w/2p – несучою частотою. Модуляція полягає в тому, що вибраний параметр піддається дії модулюючого коливання, який задає закон зміни параметра. В найпростішому випадку модуляція здійснюється за гармонійним законом. При цьому модульований параметр P представляється у вигляді

P(t)= Р_о + DP cos Wt = Р_о (1 + m cos Wt), (2.7)

де Р_о – відповідний параметр не модульованого коливання,

DP – амплітуда зміни параметра, W = 2pF – кругова частота модуляції (F – частота модуляції, тобто частота модулюючого коливання). Величину m = DP/Po називають коефіцієнтом модуляції. Частота модуляції завжди набагато менше несучої частоти, тобто F<< f (відповідно W << w).

В наземних віддалемірних пристроях найбільш часто застосовується амплітудна модуляція за гармонійним законом. Розглянемо цей випадок докладніше.

Хай не модульоване (несуче) коливання має вигляд (2.4), в якому для простоти покладемо початкову фазу j_о = 0:

S = А_о cos wt. (2.8)

При гармонійній АМ амплітуда, у відповідності з (2.7), міняється в часі згідно із законом

А(t)= Ат + DА cos Wt = Ат (1 + m cos Wt) (2.9)

 

 

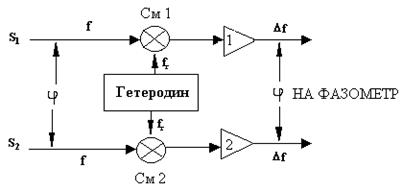
Рис.2.2. а) АМ-коливання, в якому амплітуда змінюється за гармонійним законом,

б) Частотний спектр АМ-коливання.

і рівняння АМ - коливання буде

S_AM = Ат (1 + m cos Wt) cos wt. (2.10).

Графік такого коливання показаний вище (рис.2.2,а). Застосувавши до (2.10) відому з тригонометрії формулу для добутку косинусів:

cosa · cosb = (1/2) [cos (a - b) + cos (a + b)] (2.10)

можна представити у вигляді

S_AM = А_оcos wt + (mA_o /2)cos (w - W)t + (mAo /2)cos (w + W)t. (2.11)

Обговоримо вирази (2.10) і (2.11). Формула (2.10) показує, що АМ -коливання –це коливання однієї частоти w (несучої), але із змінною амплітудою Ao(1 + mcos Wt), величина якої міняється в часі з частотою модуляції W. Формула ж (2.11) говорить про те, що АМ -коливання складається з трьох гармонійних складових з частотами w, w-W і w+W і постійними амплітудами (А_о, mAo/2 і mAо/2 відповідно). Питання «що ж є АМ -коливання насправді?» некоректне: обидва уявлення еквівалентні. В одних випадках доцільно використовувати запис (2.10), в інших – (2.11). Вираз (2.11) показує частотний спектр АМ -коливання (рис.2.2., б). Частоти w-W і w+W називаються боковими частотами. Таким чином, амплітудно-модульоване коливання полягає в загальному випадку з несучої частоти і двох бокових частот.

Цікавим окремим випадком є биття, про яке згадувалося вище – результат складання двох близьких частот w₁ і w₂. Биття – це теж АМ -коливання, але його спектр складається з двох цих частот.

Окрім гармонійної модуляції, часто використовується модуляція по прямокутному закону, коли значення модульованого параметра стрибкоподібно міняється від Р1 до Р2 і через деякий час – назад, і цей процес повторюється через однакові або різні інтервали часу. Модуляцію по прямокутному закону називають маніпуляцією. Маніпуляція фази використовується, наприклад, в глобальних супутникових навігаційних системах.

Демодуляція. Демодуляцією або детектуванням називається процес, в результаті якого з складного модульованого коливання виділяється модулююче коливання. Це процедура, зворотна модуляції. Існують детектори АМ-, ЧМ - і ФМ -коливань. Звичайно ЧМ - і ФМ коливання перетворять в АМ -коливання, яке детектується найбільш просто. Детектування АМ -коливання є нелінійною операцією, в процесі якої відбувається перемножування цього коливання або на несуче коливання, або саме на себе. Перший варіант називають синхронним детектуванням, другий – квадратичним детектуванням. В обох випадках в результаті перемножування виходить сума доданків (спектр), один з яких буде коливанням модулюючої частоти, яке виділяють за допомогою відповідного фільтру, який пропускає тільки цю частоту.

Гетеродинування. Так називають операцію перетворення частоти коливання з метою отримати коливання іншої частоти. Звичайно ця операція використовується для пониження частоти. Для здійснення гетеродинування початкове коливання частоти f змішується в радіотехнічному змішувачі з коливанням, частота якого відрізняється від f на невелику величину Df. Це коливання одержують від гетеродина – допоміжного генератора. Під змішенням звичайно розуміється перемножування коливань. В результаті перемножування утворюється спектр частот, що містить, зокрема, коливання різницевої частоти Df, яке можна виділити за допомогою відповідного фільтру. Таким чином, коливання високої частоти f перетвориться в коливання низької частоти Df. При цьому фаза низькочастотного коливання дорівнює різниці фаз змішуваних коливань.

Гетеродинування широко використовується в геодезичних фазових віддалемірах, в яких виникає задача вимірювання різниці фаз двох високочастотних сигналів. Хай є два коливання однакової високої частоти f:

S₁ = A₁ cos (2pf t + j₁) (2.12)

S₂ = А₂ cos (2pf t + j₂) (2.13)

різниця фаз яких

j = j₂ - j₁ (2.14)

необхідно виміряти. Змішавши кожне з цих коливань з коливаннями гетеродина частоти f_г

S_г = B cos (2pf_г t + j_г) (2.15)

в змішувачах См1 і См 2 (рис.2.3) і направивши вихідні сигнали змішувачів в підсилювачі низької частоти 1 і 2, отримаємо на виходах підсилювачів коливання різницевої частоти

çf - fг ê= Df вигляду

s₁ = C₁ cos [(2p Df t + (j₁ - j_г)] (2.16)

s₂ = C₂ cos [(2p Df t + (j₂ - j_г)]. (2.17)

Різниця фаз цих коливань

(j₂ - j_г) – (j₁ - j_г) = j₂ - j₁ = j (2.18)

тобто різниця фаз коливань низької (різницевої) частоти Df дорівнює різниці фаз початкових коливань високої частоти f, або, іншими словами, при гетеродинуванні фазові співвідношення не змінюються. Цей вельми важливий висновок говорить про те, що вимірювання різниці фаз двох коливань високої частоти можна, застосувавши гетеродинуванні, замінити вимірюванням різниці фаз двох низькочастотних коливань, що виконується технічно простіше і точніше.

Рис.2.3. Гетеродинна схема вимірювання різниці фаз

Кореляційна обробка негармонійних сигналів. Поняття «кореляційна обробка» застосовується до широкосмугових сигналів, тобто до сигналів, володіючих широким спектром. Метою кореляційної обробки є вимірювання часу затримки між двома однаковими, але зсунутими за часом широкосмуговими сигналами. Якщо є два такі сигнали: S1 (t) і S2 (t + t), де t - часова затримка другого сигналу щодо першого, то вводиться поняття кореляційної функції цих сигналів К_1.2, рівної

К_1.2 = < S₁(t)· S₂ (t + t)>, (2.19)

де кутові дужки означають усереднювання за великий проміжок часу – такий, який більше періоду самої низькочастотної складової спектру сигналів S₁ і S₂. Значення кореляційної функції набувають на виході корелятора – пристрою, що реалізовує операцію (2.19) перемножування і усереднювання при подачі сигналів S₁ і S₂ на його входи. Кореляційна функція К_1.2 має один різко виражений максимум при t = 0. Отже, якщо примусово змінювати затримку t до отримання максимуму вихідного сигналу корелятора і виміряти потрібно величину зміни, ми тим самим визначимо цю затримку. По суті справи, це компенсаційний спосіб, в якому індикатором моменту компенсації затримки служить максимум кореляційній функції. Позитивною якістю кореляційного методу є малий вплив шумів, супроводжуючих сигнали S₁ і S₂, на результат вимірювань. Кореляційна обробка сигналів використовується в радіоінтерферометрії з наддовгою базою (РНДБ) і при так званих кодових вимірюваннях в глобальних супутникових системах.

ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ:

Що таке частота модуляції?

2. Складаються дві когерентні хвилі однакової амплітуди, лінійно поляризовані в ортогональних площинах. Яке відношення різниці фаз цих хвиль, при якій результуюча хвиля буде мати відповідну поляризацію?