
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основи розрахунку залізобетонних конструкційСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
План 1. Стадії напружено-деформованого стану зігнутих елементів. 2. Нормативні та розрахункові опори бетону та арматури. 3. Розрахунок міцності за нормальними перерізами для елементів прямокутного профілю з одиночною арматурою 4. Три типи задач.
1. Сукупність напружень та деформацій в перерізі по всіх його ділянках називають напружено-деформованим станом (НДС). При поступовому збільшенні навантаження на елемент послідовно виникають три основні стадії НДС. Стадія І. При малих навантаженнях (згинальних моментах) напруження в бетоні та арматурі невеликі, деформації мають пружний характер. Залежність між напруженнями і деформаціями лінійна і епюри напружень як у стиснутій, так і в розтягнутій зонах трикутні (рис.12, а). При збільшенні навантаження в розтягнутій зоні бетону розвиваються пластичні деформації, епюра напружень стає криволінійною і напруження досягають межі міцності на розтягання Стадія ІІ. Оскільки
Рис.12. Стадії напружено-деформованого стану при згині: а – І; б – Іа; в – ІІ; г – ІІІ (випадок 1); д – ІІІ (випадок 2).
Стадія ІІІ – це стадія руйнування. Розрізняють два характерних випадки руйнування елементів. Випадок 1. В нормально армованих перерізах несуча здатність розтягненої арматури дещо менша за несучу здатність стиснутої зони бетону, тому напруження в арматурі раніше досягають своїх граничних значень ( Випадок 2. При перенасиченні перерізу арматурою елемент руйнується внаслідок роздавлювання бетону стиснутої зони; при цьому напруження в розтягнутій арматурі не досягають межі текучості ( 2. Клас бетону за міцністю В - це кубикова міцність, тобто межа міцності на стиск куба зі стороною 15см, витриманого в нормальних умовах 28 діб з врахуванням статистичної змінності.
Рис.13. Випробування куба для визначення класу бетону.
Для розрахунків використовують призмовуміцність Rb – це межа міцності на стиск призми зі стороною основи 15см та висотою в 4 рази більшою у віці 28 діб. Нормативна призмова міцність – це нормативний опір бетону стиску Rbn. Розрахункова призмова міцність – розрахунковий опір бетону стиску
де
Рис.14. Випробування бетонної призми на стиск.
Нормативна призмова міцність розтягу – це нормативний опір бетону розтягу Rbtn. Він у 10…20 разів менший за Rbn.. Розрахункова призмова міцність розтягу – розрахунковий опір бетону розтягу
Міцність при зрізі та сколюванні. На міцність при зрізі суттєво впливають крупні зерна заповнювача, які, потрапляючи у площину зрізу працюють як шпонки. Міцність при зрізі визначається за емпіричною формулою
Нормативний опір арматури з урахуванням розкиду міцності дорівнює найменшому контрольованому значенню текучості фізичному або умовному з вірогідністю 95%.
Виключення складає дріт класу Вр-ІІ, для якого
Рис.15. Випробування арматури на розтяг.
Розрахунковий опір арматури розтягу отримують шляхом ділення нормативного на коефіцієнт надійності за арматурою γsi.
За розрахунковий опір арматури стиску Rsc приймають опір арматури розтягу, але не більше ніж 400МПа, в деяких випадках 500МПа.
3. Передумови для визначення граничних зусиль в перерізі: 1. В розтягненій зоні бетон не працює ( 2. Напруження стиску в бетоні дорівнюють розрахунковому опору бетону стиску ( 3. Напруження розтягу в арматурі приймають рівними розрахунковому опору арматури розтягу ( 4. Деформації та напруження в арматурі визначаються в залежності від висоти стиснутої зони бетону. Для визначення внутрішніх зусиль застосовується метод перерізів, тобто елемент розрізається по нормальному перерізу, відкидається права частина та для витримки рівноваги дію відкинутої частини замінюють внутрішніми зусиллями (рис.16). В основу розрахунку покладена третя стадія НДС – стадія руйнування.
Рис. 16. Розрахункова схема нормального перерізу при розрахунках міцності прямокутних елементів з одиночним армуванням.
На рис.16 М – згинальний момент від зовнішнього навантаження;
z = h0 - x/2, (17) h0 – робоча висота перерізу – відстань від стиснутої грані бетону до центру розтягненої арматури,
h0=h-a, (18) де а – відстань від центру розтягненої арматури до розтягненої грані бетону,
а = ЗШ+ds/2. (19)
Якщо арматура розташована в два ряди
а = ЗШ+ds+(в світлі/2). (20)
Повинні бути дотримані рівняння рівноваги:
Застосуємо рівняння
Міцність нормального перерізу елементів буде забезпечена, якщо згинальний момент від зовнішніх розрахункових зусиль М не перевищуватиме розрахункової несучої здатності того самого перерізу за згинальним моментом Мu (розрахунковий момент, який може витримати переріз при досягненні ним граничного стану), тобто
Складемо рівняння рівноваги моментів відносно вісі, яка проходить через центр ваги стиснутої зони бетону:
Умова рівності нулю суми проекцій усіх нормальних зусиль на поздовжню вісь елемента має вигляд:
Вирішуючи систему цих рівнянь ми знаходимо дві невідомі х, As. Відносна висота стиснутої зони бетону Проаналізувавши рівняння (25) зрозуміло, що зі збільшенням кількості арматури збільшується площа стиснутої зони бетону З рівняння (25) знаходимо:
де Оптимальний відсоток армування становить: для балок На практиці для розрахунку прямокутних перерізів використовують таблиці (таблиця 20 [7]). Для цього вводять позначення
Для знаходження другої невідомої в рівняння (9.5) підставимо значення
В рівняння (25) підставимо значення х
Також As можна знайти з рівняння (24):
4. При розв¢язанні задач міцності можливі різні варіанти. Перший тип - перевірка міцності нормального перерізу. При цьому задано розміри поперечного перерізу, армування, характеристики міцності матеріалів та зовнішній згинальний момент. Розрахунки виконуються у наступній послідовності: - знаходимо відносну висоту стиснутої зони бетону - визначаємо Mu попередньо знайшовши в табл. 20 [7]
за x ® z і am:
- перевіряємо умову:
Другий тип - підбір перерізу робочої арматури. Дано: b, h, Rb, Rs, M. Знайти As? Розрахунок виконується у такій послідовності: - знаходимо - за am ® x, z; - перевіряємо умову - визначаємо площу арматури - здійснюємо конструювання перерізу.
Третій тип - Підбір перерізів бетону і арматури одночасно. Дано: Rb, Rs, M. Визначити: b, h, As? Послідовність розрахунку: - задаються оптимальним коефіцієнтом армування m і визначають відносну висоту стиснутої зони бетону: - за x® am; - конструктивно призначаємо b; - знаходимо робочу висоту перерізу - підраховуємо загальну висоту перерізу: - уточнюємо - за am ® x, z; - перевіряємо умову - визначаємо площу поздовжньої робочої арматури
Лекція 5
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 844; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.108.201 (0.007 с.) |

 (рис.12, б). У стиснутій зоні бетону переважають пружні деформації і епюра напружень близька до трикутної (стадія 1а) Цю стадію беруть за основу при розрахунку за утворенням тріщин.
(рис.12, б). У стиснутій зоні бетону переважають пружні деформації і епюра напружень близька до трикутної (стадія 1а) Цю стадію беруть за основу при розрахунку за утворенням тріщин. а) б) в) г) д)
а) б) в) г) д) ), в наслідок чого зменшується висота стиснутої зони бетону х. Напруження в бетоні стиснутої зони зростають і досягають граничних (
), в наслідок чого зменшується висота стиснутої зони бетону х. Напруження в бетоні стиснутої зони зростають і досягають граничних (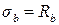 ). Руйнування носить пластичний характер (рис.12, г).
). Руйнування носить пластичний характер (рис.12, г). ) і її міцність використовується не повністю (рис.12, д). Таке руйнування носить крихкий характер.
) і її міцність використовується не повністю (рис.12, д). Таке руйнування носить крихкий характер.

 , (12)
, (12) - коефіцієнт надійності за матеріалом для бетону.
- коефіцієнт надійності за матеріалом для бетону.
 . (13)
. (13) . (14)
. (14) . (15)
. (15) .
.
 . (16)
. (16) ).
).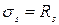 ).
).
 - рівнодіюча зусиль в стиснутому бетоні; х – висота стиснутої зони бетону;
- рівнодіюча зусиль в стиснутому бетоні; х – висота стиснутої зони бетону;  - рівнодіюча зусиль в розтягненій арматурі; z – плече внутрішньої пари сил
- рівнодіюча зусиль в розтягненій арматурі; z – плече внутрішньої пари сил (21)
(21) Складемо рівняння рівноваги моментів відносно вісі, яка проходить через центр розтягненої арматури
Складемо рівняння рівноваги моментів відносно вісі, яка проходить через центр розтягненої арматури (22)
(22) . (23)
. (23)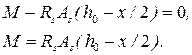 (24)
(24)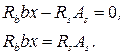 (25)
(25) , звідси
, звідси  .
. , тобто збільшується
, тобто збільшується  та х. Вочевидь існує граничне значення відносної висоти стиснутої зони бетону
та х. Вочевидь існує граничне значення відносної висоти стиснутої зони бетону  (табл.18 [7]). Цьому значенню буде відповідати граничне армування, при перевищенні якого руйнування елементу почнеться зі стиснутої зони бетону, а не з розтягненої арматури. Якщо
(табл.18 [7]). Цьому значенню буде відповідати граничне армування, при перевищенні якого руйнування елементу почнеться зі стиснутої зони бетону, а не з розтягненої арматури. Якщо 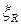 - це перший випадок руйнування, якщо
- це перший випадок руйнування, якщо  , (26)
, (26) - коефіцієнт або відсоток армування. Згідно з вимогами норм мінімальний відсоток армування залізобетонних елементів при згині має становити 0,05%.
- коефіцієнт або відсоток армування. Згідно з вимогами норм мінімальний відсоток армування залізобетонних елементів при згині має становити 0,05%. , для плит
, для плит  .
.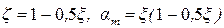 . (27)
. (27) (28)
(28) . (29)
. (29)

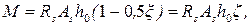 (30)
(30) .
. ;
;
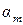 за формулою (28);
за формулою (28); ;
; за формулою (29, або 30)
за формулою (29, або 30) ;
; ;
; ;
;


