
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритми виконання операцій додавання і віднімання двійкових чиселСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Алгоритми виконання операцій додавання і віднімання в позиційній однорідній системі числення з основою k відповідає алгоритмам в звичайній десятковій системі числення. Результати операцій додавання / віднімання цифр х та у в одному розряді представляються двома цифрами: ü цифрою q результат операції у даному розряді; ü цифрою р перенесення в старшому розряді. Правила формування цифр q та р для будь-якого k можна записати наступним чином. а) для додавання б) для віднімання
q = q = х + у – k, якщо х + у ≥ k k + х – у, якщо х < у
р = р = 1, якщо х + у ≥ k - 1, якщо х < у Функції q (x, y) та р (х, у) для операцій додавання/віднімання для k =2 можна представити таблично, рис. 1.1. а) додавання б) віднімання
рис.1.1. Оскільки при виконанні операцій додавання / віднімання може виникнути переповнення розрядної сітки, тобто результат буде сформовано неправильно, тому використовують модифіковані коди. Особливістю цих кодів є наявність двох знакових розрядів, у яких знак відображається двома однаковими цифрами. Ці цифри обробляються при виконанні також як і числові розряди. Поява в знакових розрядах модифікованого коду різних цифр"01" або „10" свідчать про переповнення розрядної сітки. Приклад 1. х = -9 у = -3 Хпрм = 11,1001; Упрм = 11,0011 Хоб.м = 11,0110; Уоб.м = 11,1100
+ + Уоб.м – 11,1100 11,0010 циклічний перенос + 1
Zоб.м – 11,0011 Запишемо результат Zоб. м у прямому коді, використовуючи правила перетворення із оберненого коду в прямий. Zпрm = 11,1100 це відповідає числу-12. При виконанні модифікованого додаткового коду може з'явитися така комбінація 11.000...0 - це фіксується як переповнення розрядної сітки, тому що отримане число не вміщається в розрядній сітці. Приклад 2. х = -7 у = -9 z = -16 Хпрм= 11,0111, Упрм= 11,1001 Хдк,м – 11,1001 + + Удкм - 11,0111 Zдкм - 11,0000 Бачимо, що для представлення числа -16 потрібно 5 двійкових розрядів. Zдкм - 11,0000 Zп.к.м - 11,01111 ____ + 1 11,10000, що відповідає числу -16. Слід відмітити, що модифікований код дозволяє формувати вірний знак результату навіть при появі переповнення. Цей знак зберігається у другому (старшому) знаковому розряді. 01 - свідчать про позитивне переповнення розрядної сітки 10 - свідчать про від'ємне переповнення розрядної сітки. Алгоритм додавання / віднімання чисел з фіксованою комою у прямих та додаткових кодах розглянемо на прикладах. Приклад 3. х = ±15, у = ±7 а) х + у Хпрм = Хдкм = 00,01111 Упрм = Уд.к.м = 00,00111 z = 22 00,01111 + 00,00111 00.10110, що відповідає числу 22. b) х - у; Хд.к.м = 00,01111; У д.к.м = 11,11001 z = 8
00,0111 + 11,11001 Zп.к.м = 00,01000, що відповідає +8 с) - х + у; Хд.к.м = 11,10001; У д.к.м = 00,00111 z = - 8 11,10001 + 00,00111 Zп.к.м = 11,11000 → Znp.м = 11,01000, що відповідає -8 d) –x - y; Хд.к.м = 11,10001; У д.к.м = 11,11001; z = -22
11,10001 + 11,11001 Zп.к.м = 11,01010 → Znp.м = 11,10110, що відповідає -22 Алгоритм додавання/ віднімання чисел з ,,блукаючою" комою будемо розглядати для k = 2, тоді операнди X та У можна записати так X = 2А х, У = 2Ву, де А, В порядок операндів; X, У, які представлені „m" розрядами; Мантиси х та у є n - розрядні правильні нормалізовані дроби, тобто 1/2≤|х|<1, 1/2≤|у|<1. Операція додавання (віднімання) з „блукаючою комою" здійснюється в декілька етапів: — вирівнюються порядки доданків; молодший порядок збільшується до більшого, при цьому відбувається корекція мантиси числа, яке перетворюється; — виконується перетворення мантис в додаткові коди; — виконується додавання мантис за правилами, які розглядались для чисел з фіксованою комою; — до отриманої суми дописується порядок доданків і якщо буде потрібно виконується нормалізація результату. Можливі два випадки денормалізації: а) денормалізація вліво відповідає переповненню розрядної сітки; б) денормалізація вправо, яка виникає, коли у прямому коді мантиси після Приклад 4. Потрібно додати два числа X = + 0,10101 ∙ 10101; У = - 0,11001 ∙ 10011 - Вирівнюємо порядок числа В до порядку числа А У = - 0,0011001 ∙ 10+101 Оскільки РХдоп.м = 00,101 + РУдоп.м = 11,101 00, 010 Рх > Ру на 2, то виконуємо зсув вправо на 2р. мантиси числа У.
— Додаємо мантиси чисел X та У в модифікованому додатковому коді: Хдм = 00,1010100 + Улм = 11,1100111 00,0111011 це прямий код додатної мантиси. Результат отримали в ненормалізованій формі, оскільки після коми розряд мантиси має нульове значення. Для нормалізації цього числа необхідно зсунути всі розряди мантиси вліво на один розряд та зменшити на одиницю значення порядку. Запишемо результат: 00,1110110 • 10100 Цей результат буде розміщено в розрядній сітці обчислювального пристрою.
ДОМАЩНЄ ЗАВДАННЯ. 3.1. Вивчити за конспектом та підручником правила отримання прямих, обернених та додаткових модифікованих кодів як для додатних так і для від’ємних чисел. 3.2. Записати у прямому, оберненому та додатковому кодах числа ± 15 та ±13. 3.3. Записати у прямому, оберненому та додатковому модифікованих кодах числа ±22 та ±27. ВИКОНАННЯ РОБОТИ. 4.1. Скласти цілі 10-ві числа А, В, С, D за наступним правилом А = 27 + (# - 1)24 + **; B= 28- (# - l)24 - **; С= 27 + (# - 1)24 + @; D = 28 - (# - l)24- @ # - друга цифра номера групи ** - дві останні цифри студентського квитка @ - дорівнює сумі цифр у числі # 19** Наприклад, число # 19** складає 41927, тоді @ = 4+1+9+2+7=23 4.2. Перевести числа, отримані в п.4.1. та 4.2., в двійкову систему числення 4.3. Записати у прямому, оберненому та додатковому модифікованих кодах двійкові числа ±А, ±В, ±С, ±D, які були отримані при виконанні завдання п.4.2. Результат представити у вигляді наступної таблиці:
4.4. Скласти цифрові діаграми виконання операцій А+В; -В+С; С-D; -С-А, використовуючи модифіковані прямий, обернений та додатковий коди. Відмітити можливі випадки переповнення розрядної сітки. Зробити перевірку отриманих результатів, шляхом їх переведення в десяткову систему. Результати виконання записати у таблицю, наприклад:
КОНТРОЛЬНІ ЗАПИТАННЯ. 5.1. Які форми представлення двійкових чисел ви знаєте, наведіть приклади. 5.2. Переваги та недоліки представлення чисел з фіксованою (блукаючою) комою. 5.3. Яке двійкове число називається нормалізованим? 5.5. Запишіть етапи виконання отримання прямого, оберненого та додаткового коду для додатного (від’ємного) числа. 5.7. За допомогою чого в ККС можна від слідкувати переповнення розрядної сітки. Що для цього використовується. 5.8. Запишіть етапи виконання додавання / віднімання двійкових чисел з блукаючою комою. 5.9. Додати в модифікованому додатковому коді двійкові числа з блукаючою комою: a) A = - 0,110011 ∙ 211; В = - 0,100001 ∙ 2 -10 b) А = 0,101101 ∙ 2101; В = - 0,100101 ∙ 2 -10 c) А = - 0,100010 ∙ 2-11; В = 0,111101 ∙ 2 -111 ЗМІСТ ЗВІТУ 6.1. Тема та мета практичної роботи. 6.2. Виконання домашнього завдання. 6.3. Короткий звіт за пунктами виконаної лабораторної роботи. 6.4. Відповіді на контрольні запитання.
ЛАБОРАТОРНА РОБОТА №2
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1802; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.163 (0.01 с.) |

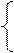
 x + y, якщо х + у < k x - y, якщо х ≥ у
x + y, якщо х + у < k x - y, якщо х ≥ у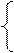
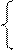 0, якщо х + у < k 0, якщо х ≥ у
0, якщо х + у < k 0, якщо х ≥ у

 Хоб.м – 11,0110
Хоб.м – 11,0110

 відкидається 1
відкидається 1 відкидається 1
відкидається 1


