
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коледж інформаційних систем і технологійСодержание книги
Поиск на нашем сайте
КОЛЕДЖ ІНФОРМАЦІЙНИХ СИСТЕМ І ТЕХНОЛОГІЙ ДЕРЖАВНОГО ВИЩОГО НАВЧАЛЬНОГО ЗАКЛАДУ “КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ імені Вадима Гетьмана”
Збірник лабораторних робіт з дисципліни: „Комп’ютерна схемотехніка”
для студентів спеціальностей:
Зміст Пояснювальна записка...................................................................................................................... 3 Перелік лабораторних робіт включених у збірник.................................................................... 10 Лабораторна робота №1.................................................................................................................. 11 Лабораторна робота №2.................................................................................................................. 15 Лабораторна робота №3.................................................................................................................. 21 Лабораторна робота №4.................................................................................................................. 29 Лабораторна робота №5.................................................................................................................. 38 Лабораторна робота №6.................................................................................................................. 43 Лабораторна робота №7.................................................................................................................. 47 Лабораторна робота №8.................................................................................................................. 55 Лабораторна робота №9.................................................................................................................. 57 Рекомендована література............................................................................................................. 61 ПОЯСНЮВАЛЬНА ЗАПИСКА
Збірник лабораторних робіт містить лабораторні роботи з предмету «Комп’ютерна схемотехніка». Лабораторні роботи призначені для: ¨ознайомлення студентів з принципом роботи логічних схем та найпростіших схем цифрових автоматів; ¨отримання навичок використання синтезу логічних схем у різних базисах та аналізувати їх роботи; ¨ознайомлення студентів з типами та класифікацією цифрових пристроїв, способами синтезу цих пристроїв та їх застосуванням при побудові різноманітних цифрових схем;
¨отримання навичок побудови найпростіших та складних цифрових пристроїв, модулів пам’яті з заданою ємністю; ¨ набуття навиків їх контролю та діагностики; ¨ отримання навичок дослідження роботи пристроїв комбінаційного та послідовнісного типів, які використовуються в сучасній обчислювальній техніці. Підготовка до лабораторних робіт частково передбачає самостійну роботу студента. Теоретичні положення, необхідні для їх ефективного виконання наведені в ході опису робіт та в кінці збірника присутній перелік рекомендованої літератури та посилань.
ПЕРЕЛІК ЛАБОРАТОРНИХ РОБІТ ВКЛЮЧЕНИХ У ЗБІРНИК
ЛАБОРАТОРНА РОБОТА №1 ТЕМА: ВИКОНАННЯ ОПЕРАЦІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ ЧИСЕЛ З ФІКСОВАНОЮ ТА ПЛАВАЮЧОЮ КОМОЮ
МЕТА РОБОТИ 1.1 Ознайомитись із зображенням чисел в комп’ютерній арифметиці в форматі з фіксованою комою. 1.2. Ознайомитись із зображенням чисел в комп’ютерній арифметиці в форматі з плаваючою комою. 1.3. Ознайомитись з представленням чисел в прямому, оберненому та додатковому кодах. 1.4. Ознайомитись з виконанням операцій додавання та віднімання чисел з фіксованою комою. 1.5. Ознайомитись з виконанням операцій додавання та віднімання чисел з плаваючою комою. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ Форми представлення чисел в комп’ютерах Будь-яке число можна записати різними формами, наприклад Х=0,0357 можна записати так 357*10-4; 0,036; 3,57*10-2 і т.д. Різноманітність форми у записі одного числа може служити причиною труднощів для роботи цифрових пристроїв. Щоб цього уникнути використовують форму запису числа. Сучасні універсальні ККС використовують дві форми представлення чисел:
Наприклад, машинне число можна записати так
Розглянемо представлення числа з фіксованою комою. Зображення числа має постійну розрядність, а положення коми фіксується в визначеному місці відносно розрядів числа [або перед старшим розрядом(рис.1.) або після молодшого(рис.2.)] Вірний дріб -1<[AФ]<1, то А=[AФ]КА Діапазон чисел від ±(1-2-31) до ±2-31
0.111…1=1-2-31 – найбільше позитивне число 0.000…1=2-31 – найменше позитивне число Діапазон чисел 1≤|x|≤231-1
При виконанні на ЕОМ обчислювань необхідно щоб усі вихідні та отримані дані не виходили за діапазон чисел, які представлені в розрядній сітці. Для цього при програмуванні задачі дані записуються з відповідними масштабними коефіцієнтами. Використання чисел з фіксованою комою дозволяє спростити схеми ЕОМ, підвищити її швидкодію, але створює труднощі при програмуванні.
Представлення числа з блукаючою комою в загальному вигляді має вид:
Для двійкових чисел вираз буде записаний так Х=2Р*q; |q|<1 Розглянемо приклад: Нехай слово має 32 2х-розрядів, а число “Х” зображується у машині 2м словом а0в0в1…в6а1а2…а24 та має такий формат
в0…в6 – використовуються для представлення порядку, при цьому розряд в0 зображує знак порядку, розряди в1…в6 – модуль порядку. Розряди а0…а24 – зображують мантису, де а0 – знак мантиси. Двійкове число Х=2Р*q називають нормалізованим, якщо у старшому розряді мантиси записана “1”. Порядок (в0…в6) має 7 розрядів, то порядок може бути від -63 до 63
Тому у розрядній сітці може бути представлено число від -263 до -264 і від 263 до 2-64, що значно перевищує діапазон чисел з фіксованою комою для 32-розрядних слів. Представлення чисел з блукаючою комою використовується в ККС, які обслуговують рішення задач науково-технічного характеру. В МП-х засобах ОТ (МП має короткий формат даних, наприклад 16р.), звичайно використовують форму представлення чисел з фіксованою комою. Робота ж з числами з блукаючою комою в МП засобах реалізується як окремий режим, який забезпечується програмним способом.. Нормальна форма представлення числа має великий діапазон відображення чисел та є основною в сучасних ЕОМ ДОМАЩНЄ ЗАВДАННЯ. 3.1. Вивчити за конспектом та підручником правила отримання прямих, обернених та додаткових модифікованих кодів як для додатних так і для від’ємних чисел. 3.2. Записати у прямому, оберненому та додатковому кодах числа ± 15 та ±13. 3.3. Записати у прямому, оберненому та додатковому модифікованих кодах числа ±22 та ±27. ВИКОНАННЯ РОБОТИ. 4.1. Скласти цілі 10-ві числа А, В, С, D за наступним правилом А = 27 + (# - 1)24 + **; B= 28- (# - l)24 - **; С= 27 + (# - 1)24 + @; D = 28 - (# - l)24- @ # - друга цифра номера групи ** - дві останні цифри студентського квитка @ - дорівнює сумі цифр у числі # 19** Наприклад, число # 19** складає 41927, тоді @ = 4+1+9+2+7=23 4.2. Перевести числа, отримані в п.4.1. та 4.2., в двійкову систему числення 4.3. Записати у прямому, оберненому та додатковому модифікованих кодах двійкові числа ±А, ±В, ±С, ±D, які були отримані при виконанні завдання п.4.2. Результат представити у вигляді наступної таблиці:
4.4. Скласти цифрові діаграми виконання операцій А+В; -В+С; С-D; -С-А, використовуючи модифіковані прямий, обернений та додатковий коди. Відмітити можливі випадки переповнення розрядної сітки. Зробити перевірку отриманих результатів, шляхом їх переведення в десяткову систему. Результати виконання записати у таблицю, наприклад:
КОНТРОЛЬНІ ЗАПИТАННЯ. 5.1. Які форми представлення двійкових чисел ви знаєте, наведіть приклади. 5.2. Переваги та недоліки представлення чисел з фіксованою (блукаючою) комою. 5.3. Яке двійкове число називається нормалізованим? 5.5. Запишіть етапи виконання отримання прямого, оберненого та додаткового коду для додатного (від’ємного) числа. 5.7. За допомогою чого в ККС можна від слідкувати переповнення розрядної сітки. Що для цього використовується. 5.8. Запишіть етапи виконання додавання / віднімання двійкових чисел з блукаючою комою. 5.9. Додати в модифікованому додатковому коді двійкові числа з блукаючою комою: a) A = - 0,110011 ∙ 211; В = - 0,100001 ∙ 2 -10 b) А = 0,101101 ∙ 2101; В = - 0,100101 ∙ 2 -10 c) А = - 0,100010 ∙ 2-11; В = 0,111101 ∙ 2 -111 ЗМІСТ ЗВІТУ 6.1. Тема та мета практичної роботи. 6.2. Виконання домашнього завдання. 6.3. Короткий звіт за пунктами виконаної лабораторної роботи. 6.4. Відповіді на контрольні запитання.
ЛАБОРАТОРНА РОБОТА №2
МЕТА РОБОТИ 1.1 Ознайомитись з алгоритмами множення в ЕОМ.. 1.2. Ознайомитись з алгоритмами ділення в ЕОМ.. 1.3. Ознайомитись з виконанням операцій множення та ділення для чисел з фіксованою та плаваючою комою. ДОМАШНЄ ЗАВДАННЯ. 3.1. Вивчити за конспектом та підручником правила множення чисел за I, II, III та IV основними алгоритмами. 3.2. Вивчити за конспектом та підручником алгоритми ділення без відновлення залишку. 3.3. Скласти цифрову діаграму ділення чисел 20/32 на 27/32 без відновлення залишку. Зробити перевірку отриманого результату.
ВИКОНАННЯ РОБОТИ. 4.1. Скласти цифрові діаграми множення двійкових чисел X на Y та V на W відповідно до таблиці 2.1 (варіант визначається по порядковому номері в журналі) Таблиця 2.1
4.2. Зробити перевірку вірності отриманих добутків, шляхом їх переведення у десяткову систему. 4.3. Скласти цифрову діаграму ділення чисел А та В без відновлення залишку відповідно до таблиці 2.2 (варіант визначається по останній цифрі студентського квитка) Таблиця 2.2
КОНТРОЛЬНІ ЗАПИТАННЯ. 5.1. Яку арифметичну операцію визначає зсув інформації вліво на один, два розряди?. 5.2. Яку арифметичну операцію визначає зсув інформації вправо на один, два розрядів?. 5.3. Який з 4 основних алгоритмів множення є найшвидшим? 5.5. Які елементарні операції лежать в основі алгоритмів множення та ділення? 5.7. Що є недоліком алгоритму ділення без відновлення залишку? 5.8. Запишіть етапи виконання множення / ділення двійкових чисел з блукаючою комою. 5.9. Наведіть по два приклади на реалізацію множення / ділення чисел з плаваючою комою ЗМІСТ ЗВІТУ 6.1. Тема та мета практичної роботи. 6.2. Виконання домашнього завдання. 6.3. Короткий звіт за пунктами виконаної лабораторної роботи. 6.4. Відповіді на контрольні запитання. 6.5. Зробити висновки.
ЛАБОРАТОРНА РОБОТА №3 МЕТА РОБОТИ 1.1. Вивчити і практично закріпити основні правила і закони алгебри логіки 1.2. Закріпити знання про перетворення логічних виразів методами Квайна-МакКласкі і карти Карно (діаграм Вейча). Мінімізація методом Квайна. Мінімізацію по Квайну потрібно починати із ДДНФ функції. Якщо функція задається в довільній формі, то її необхідно перетворити до ДДНФ. Для цього член в записі функції, який не містить якого-небудь аргумента, множимо на логічну одиницю, і таким чином одержуємо два члена, які містять весь набір аргументів, а потім до функції застосовуємо операції склеювання і поглинання, щоб одержати скорочену ДНФ функцію. Розглянемо етапи мінімізації логічної функції В даній функції У результаті застосування правила склеювання у виразі логічної функції зменшується число підсумовуваних добутків і число змінних. Таким чином, мінімізація функцій Буля проводиться за допомогою законів і теорем алгебри логіки, теореми де Моргана, закона подвійного заперечення і правил поглинання і склеювання. Мінімізація функцій Буля за допомогою карт Карно (табличний метод). Карта Карно — це прямокутник, розбитий на квадрати (комірки), число яких дорівнює 2n, де n- число логічних змінних. Структура карт Карно для 2-х, 3-х, 4-х змінних показана на рис. 3.1.
Рис.3.1. Карти Карно: а) для функції 2-х аргументів; б) для функції 3-х аргументів; в) для функції 4-х аргументів; Комірки карти відповідають значенням вхідних змінних. Наприклад, верхній рядок карти для функції 3-х змінних відповідає "1", тобто значення х1=1, а нижній рядок - нульовому значенню х1=0 кожний стовпчик характеризується значенням двух змінних х2 і х3. Для табличної заданої функції у комірки карта Карно проставляють значення функції для відповідних наборів аргументів, рис.2. Пошуки мінімальної форми функції зводяться до визначення областей, які містять по 2k комірок, де 2- число, k-ціле число (0, 1, 2...). В області об'єднуються сусідні комірки, які відповідають сусіднім елементарним добуткам рис.3.
Рис. 3.1 Такій мінімізації відповідає вираз:
Рис. 3.2. Карти Карно і мінімальний запис логічних функцій: а) для 3-х змінних; б),в) для 4-х змінних
Аналізуючи карти Карно, рис. 3, бачимо, що одна і таж комірка (наприклад, комірка з координатами х2х3) може покриватися два або декілька разів. Таким чином, формула, одержана в результаті мінімізації логічної функції за допомогою карт Карно, містить суму стількох елементарних добутків, скільки областей є в карті. Чим більше комірок в області, тим меньше змінних міститься у відповідному йому симентарному добутку.
ДОМАШНЄ ЗАВДАННЯ. 3.1. Вивчити за опорним конспектом способи мінімізації логічних функцій. 3.2.Довести тотожність, відмічаючи закон і правила алгебри логіки застосовувані на кожному кроці перетворення: 3.3. Логічна функція задана картою Карно. Вибрати правильну відповідь, що відповідатиме мінімізованій формі. На карті Карно проставити відповідні змінні та виділити відповідні області при мінімізації..
ВИКОНАННЯ РОБОТИ. 4.1. Визначити свій варіант логічної функції. Для цього необхідно свій порядковий номер по журналу перевести в двійкову систему числення і записати п'ятьма розрядами у вигляді слова А5А4А3А2А1. Визначивши значення Аі, підставити їх в таблицю 5. Наприклад, якщо порядковий номер по журналу1010=010102, то А5= 0, А4= 1, А3= 0, А2= 1, А1 = 0
Таблиця 3.3.
4.2. Продовжити роботу по схемі алгоритму
4.3. Порівняти мінімізовані функції отримані в п.4.2, зробити відповідні висновки. 4.4. Дати відповіді на контрольні запитання. 4.5. Зробити висновки по роботі.
КОНТРОЛЬНІ ЗАПИТАННЯ. 5.1. Які існують способи задания логічних функцій? Наведіть приклади функцій заданих різними способами. 5.2. Використовуючи основні закони Булевої алгебри, спростити наступні вирази:
5.3. Отримайте заперечення наступних виразів та спростіть їх:
5.4. Мінімізуйте логічні функції
ЗМІСТ ЗВІТУ 6.1. Тема та мета практичної роботи. 6.2. Виконання домашнього завдання. 6.3. Звіт за пунктами виконаної практичної роботи. 6.4. Відповіді на контрольні запитання. 6.5. Висновки.
ЛАБОРАТОРНА РОБОТА №4 МЕТА РОБОТИ 1.1. Вивчити методи проектування комбінаційних схем 1.2. Ознайомитись з особливостями будування схем логічних пристроїв на реальних ІМС. 1.3. Оволодіти методами контролю та діагностики роботи логічних пристроїв ДОМАШНЄ ЗАВДАННЯ. 3.1. Вивчити основні теоретичні відомості даної лабораторної роботи. 3.2. Проведіть мінімізацію логічних функцій та побудуйте схему в базисі І, АБО, НЕ.
3.3. Напишіть булеві вирази по логічних схемах.
3.4. Побудуйте логічні схеми для недовизначених функцій пред'явленими картами Карно.
ВИКОНАННЯ РОБОТИ. 4.1. Побудувати логічну схему для мінімізованої функції f (Л.Р.№3, п. 4.2.) в базисі І, АБО, НЕ. 4.2. Побудувати логічну схему для мінімізованої функції f (Л.Р.№3, п. 4.2.) в базисі І- НЕ на ІМС серії КР1533 (див додаток). 4.3. Побудувати логічну схему для мінімізованої функції f (Л.Р.№3, п. 4.2.) в базисі АБО-НЕ на ІМС серії КР1533. (див.додаток) 4.4. Визначте і запишіть на логічній схемі в базисі І, АБО, НЕ значення логічних сигналів на виході кожного логічного елементу і на виході схеми, якщо на її вході х1=0; х2=1; х3=0 4.5. Визначте і запишіть на логічній схемі в базисі І-НЕ (ІМС серії КР1533) значення логічних сигналів на виході кожного логічного елементу і на виході схеми, якщо на її вході х1=1; х2=0; х3=1. 4.6. Визначте і запишіть на логічній схемі в базисі АБО-НЕ (мікросхеми серії KP 1533) значення логічних сигналів на виході кожного логічного елементу і на виході схеми, якщо на її вході х1=0; х2=1; х3=1. 4.7. Зібрати на стенді схеми представлені на рис.4.10 та 4.11. Скласти таблиці істинності, табл..4.2 і 4.3, та записати аналітичну форму функцій, що реалізовані на цих схемах. Перевірити роботу схеми для чого вхідні сигнали подати від тумблерів, що є на стенах, а вихідні – підключити до елементів індикації. Отримані значення внеси до табл.4.2. і 4.3. відповідно. 4.8. Дати відповіді на контрольні запитання. 4.9. Зробити висновки по роботі.
КОНТРОЛЬНІ ЗАПИТАННЯ. 5.1. По заданим виразам побудуйте схему в базисі І, АБО, НЕ
5.2. 3адати роботу логічного пристрою логічним виразом та таблицею істинності. Визначити значення сигналу на виході, якщо х1 = 1, х2 = 0, х3 = 0, х4 = 1
5.3. Визначити та записати вихідні сигнали для кожного вхідного сигналу /а,b,с,d,e,f/
ЗМІСТ ЗВІТУ 6.1. Тема та мета практичної роботи. 6.2. Виконання домашнього завдання. 6.3. Звіт за пунктами виконаної практичної роботи. 6.4. Відповіді на контрольні запитання. 6.5. Висновки.
ЛАБОРАТОРНА РОБОТА №5
МЕТА РОБОТИ 1.1. Вивчити елементну базу дешифраторів 1.2. Ознайомитись з роботою лінійного дешифратора 1.3. Дослідити двоступеневий дешифратор 1.4. Отримати практичні навики роботи із довідниковою літературою 1.5. Оволодіти методами контролю та діагностики роботи комбінаційних пристроїв ДОМАШНЄ ЗАВДАННЯ 3.1. Вивчити основні теоретичні відомості лабораторної роботи та опорного конспекту. 3.2. З довідника виписати функціональне призначення і навести УГП мікросхеми, яка пропонується за варіантом (Таблиця 5.3). Номер варіанту співпадає з парністю/непарністю порядкового номеру по журналу (парні номери пишуть 1 варіант, непарні - 2) Таблиця 5.3
3.3. Дати визначення одноступеневого(лінійного дешифратору). 3.4. Дати визначення двохступеневого дешифратора.
ВИКОНАННЯ РОБОТИ 4.1. Скласти схему, яка подана на рис. 5.4 і перевірити її роботу. Скласти таблицю істинності, табл.5.4. Вхідні сигнали подавати від тумблерів на стенді, а виводи підключити до елементів індикації.
4.2. Зібрати схему, яка подана на рис.5.5 і перевірити роботу першої ступені DC1, DC2, а також роботу чотирьох входового дешифратора. Отримані дані занести в таблицю 5.5. 4.3. Зробити висновки по роботі.
Двохступеневий дешифратор
Рис.5.5. Схема електрична функціональна
Таблиця 5.5
|

 , заданій в ДДНФ.
, заданій в ДДНФ.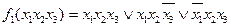 - об'єднуємо елементарні добути, отримаємо -
- об'єднуємо елементарні добути, отримаємо -  , маємо
, маємо 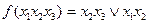 .
.

 . Карти Карно можна уявно звертати, що дасть змогу побачити найбільш короткі імплеканти результуючі кон'юнкції, рис.3.2.
. Карти Карно можна уявно звертати, що дасть змогу побачити найбільш короткі імплеканти результуючі кон'юнкції, рис.3.2.
 .
. 2.
2. 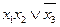 3.
3.  4.
4.  5.
5. 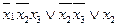
 2.
2.  3.
3. 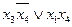 4.
4. 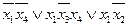 5.
5. 



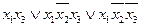






 Рис. 4.10
Рис. 4.10
 Рис.4.11
Рис.4.11

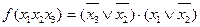


 Рис. 5.4. Схема електрична функціональна
Рис. 5.4. Схема електрична функціональна




