
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Допускаемое контактное напряжениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Допускаемое контактное напряжение
Для косозубых передач с твердостью колеса
При этом должно выполняться условие:
Допускаемые напряжения
Предел контактной выносливости Таблица 2.3 Предел контактной выносливости
Коэффициент долговечности Коэффициент запаса прочности
где
Таблица 2.4 Значение коэффициента
Допускаемые напряжения изгиба
Допускаемые напряжения изгиба зубьев шестерни
Предел выносливости Таблица 2.5 Предел выносливости
Коэффициент долговечности:
где Требуемый ресурс Коэффициент запаса прочности равен произведению трех частных коэффициентов запаса:
Коэффициент запаса прочности Для нитроцементированных и цементированных (с автоматическим регулированием процесса) зубчатых колес коэффициент запаса прочности Коэффициент запаса прочности Коэффициент запаса прочности
Проектировочный расчет цилиндрических зубчатых передач Исходные данные для проектировочного расчета Исходные данные для проведения проектного расчета зубчатой передачи: · вращающий момент на шестерне (т.е. наибольший из действующих моментов при нормально протекающем процессе эксплуатации) · частота вращения шестерни · передаточное число u; · требуемый ресурс передачи
Кроме того, должны быть известны особые технологические и эксплуатационные требования:
· условия смазывания (закрытая или открытая передача); · тип передачи (с наружным или внутренним зацеплением); · схема механизма (редуктора), уточняющая расположение рассчитываемой передачи относительно опор; · ограничения по габаритным размерам; · масштаб производства (массовое или индивидуальное); · ограничения по шумности; · ограничения по применяемым материалам, по точности обработки и т.д.
Предварительные расчеты 2.11.2.1 Предварительное (в первом приближении) значение межосевого расстояния
где знак «+» относят к внешнему зацеплению, знак «–» – к внутреннему;
u – передаточное число. Коэффициент K в зависимости от твердости поверхности H 1 и H 2 зубьев шестерни и колеса соответственно имеет следующие значения: Твердость H H 1 £ 350 HB H 1 ³ 45 HRC H 1 ³ 45 HRC H 2 £ 350 HB H 2 £ 350 HB H 2 ³ 45 HRC Коэффициент K 10 8 6 Примечание: Для обеспечения максимальной компактности передачи применяются колеса с твердостью зубьев H 1, H 2 ³ 45 HRC. Но они требуют более дорогих сталей, повышенной точности изготовления и отличаются высокой стоимостью изготовления. Применение колес с твердостью зубьев H 1, H 2 £ 350 HB облегчает механическую обработку, улучшает прирабатываемость (т.е. требуется менее высокая точность) и значительно снижает себестоимость изготовления, но значительно увеличивает габариты и массу передачи. 2.11.2.2 По предварительному межосевому расстоянию и приведенными выше рекомендациями, надлежит, прежде всего, определить размеры заготовок шестерни и колеса, что необходимо для определения технологии изготовления (см. п. 2.3 и п. 2.4), и выбрать материалы для колес и их термообработку (твердость поверхности и сердцевины зубьев шестерни
2.11.2.3 Предварительная окружная скорость:
По предварительной окружной скорости можно оценить быстроходность передачи, выбрать вид передачи – прямозубая, косозубая или шевронная (см. п. 2.2), назначить степень точности изготовления (см. п. 2.5 и табл. 2.1).
Коэффициент нагрузки В расчетах на контактную выносливость при действии постоянной нагрузки в качестве расчетной нагрузки принимают номинальный момент на шестерне
В расчетах на изгибную выносливость коэффициент нагрузки
2.11.3.1 Коэффициенты Таблица 2.6 Коэффициента динамической нагрузки
2.11.3.2 Коэффициенты
Значения коэффициента ширины Таблица 2.7 Значения коэффициента ширины
Меньшие значения
2.11.3.3 Коэффициенты для прямозубых передач:
для косозубых передач:
где а - коэффициент, равный 0,15 для зубчатых колес с твердостью
Последовательность расчета 2.11.4.1 Межосевое расстояние (второе приближение):
Коэффициент ширины Коэффициент нагрузки Допускаемое напряжение Полученное значение 2.11.4.2 Ширина венца колеса равна рабочей ширине передачи, т.е. Ширину венца шестерни принимают большую, чем у колеса, мм: 2.11.4.3 Нормальный модуль зубчатых колес определяют (с дальнейшим округлением по ГОСТ 9563-60) из следующих соотношений:
Значение коэффициента
Таблица 2.8 Рекомендуемые значения
Минимальный модуль
где
Допускаемое напряжение изгиба для колеса Максимально допустимый модуль
Полученное при расчете значение m округляют до ближайшего большего (согласно ГОСТ 9563-60), мм: 1-й ряд - 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10 2-й ряд - 1,12; 1,37; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9
2.11.4.4 Суммарное число зубьев для прямозубых передач определяют по формуле:
Учитывая, что Для косозубых передач – минимальный угол наклона зубьев:
Для шевронных передач угол Затем определяют суммарное число зубьев по формуле:
Полученное значение
2.11.4.5 Числа зубьев шестерни
(значение Для прямозубых и косозубых зубчатых колес, нарезанных без смещения инструмента ( Число зубьев колеса
2.11.4.6 Фактическое значение передаточного числа u с точностью до 0,01:
2.11.4.7 Определение геометрических параметров передачи: делительный диаметр: диаметр вершин зубьев: диаметр впадин зубьев: 2.11.4.8 Для расчета валов и подшипников определяют силы в зацеплении (рис. 2.9):
где
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.168 (0.015 с.) |

 , принимаемое для расчетов зависит от твердости зубьев шестерни и колеса. Для всех прямозубых и для косозубых передач с твердостью
, принимаемое для расчетов зависит от твердости зубьев шестерни и колеса. Для всех прямозубых и для косозубых передач с твердостью 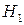 и
и  ≥ 350 HB
≥ 350 HB  и колеса
и колеса  :
: .
. > 350 НВ:
> 350 НВ: .
. .
. .
.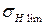 выбирают по табл. 2.3, в зависимости от материала зубчатого колеса и средней твердости поверхности зубьев Н, равной полусумме верхнего и нижнего значений их твердости. Например, при твердости зубьев шестерни
выбирают по табл. 2.3, в зависимости от материала зубчатого колеса и средней твердости поверхности зубьев Н, равной полусумме верхнего и нижнего значений их твердости. Например, при твердости зубьев шестерни 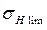 , МПа
, МПа



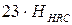
 определяют по табл. 2.4.
определяют по табл. 2.4. равен произведению трех частных коэффициентов запаса:
равен произведению трех частных коэффициентов запаса:
 – минимальный коэффициент запаса: 1,1 - для зубчатых колес с однородной структурой материала (нормализованных, улучшенных, объемно закаленных); 1,2 - для зубчатых колес с поверхностным упрочнением;
– минимальный коэффициент запаса: 1,1 - для зубчатых колес с однородной структурой материала (нормализованных, улучшенных, объемно закаленных); 1,2 - для зубчатых колес с поверхностным упрочнением; – коэффициент запаса: 1,13 - для передач, выход которых из строя связан с тяжелыми последствиями, 1,0 - для остальных случаев;
– коэффициент запаса: 1,13 - для передач, выход которых из строя связан с тяжелыми последствиями, 1,0 - для остальных случаев; – коэффициент запаса, учитывающий упрощения (допущения) при определении действующих и допускаемых напряжений (
– коэффициент запаса, учитывающий упрощения (допущения) при определении действующих и допускаемых напряжений ( ,
,  = 2,6.
= 2,6.

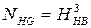 Если твердость задана в HRC, то ее перевод можно осуществить по рис 2.12.
Если твердость задана в HRC, то ее перевод можно осуществить по рис 2.12.

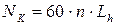 ,
где
,
где  – ресурс передачи в часах.
– ресурс передачи в часах.

 и колеса
и колеса  определяют по формуле:
определяют по формуле: .
. при ''отнулевом" (пульсационном) цикле нагружений выбирают по табл. 2.5, в зависимости от материала и твердости зубьев.
при ''отнулевом" (пульсационном) цикле нагружений выбирают по табл. 2.5, в зависимости от материала и твердости зубьев.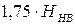


 ,
, 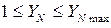 ,
, = 6,
= 6, 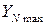 = 4 – для нормализованных и улучшенных зубчатых колес;
= 4 – для нормализованных и улучшенных зубчатых колес; 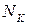 –см. табл. 2.4.
–см. табл. 2.4.
 = 1,7.
= 1,7.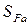 = 1,3 для передач, выход которых из строя связан с тяжелыми последствиями; для обычных условий
= 1,3 для передач, выход которых из строя связан с тяжелыми последствиями; для обычных условий 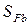 = 1,1...1,3 при определении действующих и допускаемых напряжений.
= 1,1...1,3 при определении действующих и допускаемых напряжений. , Н×м;
, Н×м; , об/мин;
, об/мин; , мм:
, мм: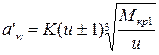 ,
, и колеса
и колеса  , МПа) (см. п. 2.9):
, МПа) (см. п. 2.9): мм,
мм,  мм.
мм. , м/сек.
, м/сек. :
: .
. :
: .
. ,
,  , учитывающие внутреннюю динамическую нагрузку, определяют по табл. 2.6, в зависимости от вида передачи, твердости колес, окружной скорости
, учитывающие внутреннюю динамическую нагрузку, определяют по табл. 2.6, в зависимости от вида передачи, твердости колес, окружной скорости  и степени точности.
и степени точности. ,
, 
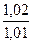



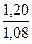


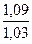












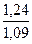

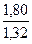






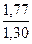



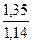
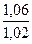
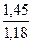





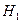 и
и  > 350 HB;
Б –
> 350 HB;
Б –  ,
,  , учитывающие неравномерность распределения нагрузки по длине контактных линий, определяют по номограммам (рис. 2.13) в зависимости от коэффициента ширины
, учитывающие неравномерность распределения нагрузки по длине контактных линий, определяют по номограммам (рис. 2.13) в зависимости от коэффициента ширины  , схемы передачи и твердости зубьев. Значение
, схемы передачи и твердости зубьев. Значение  вычисляют по формуле:
вычисляют по формуле:
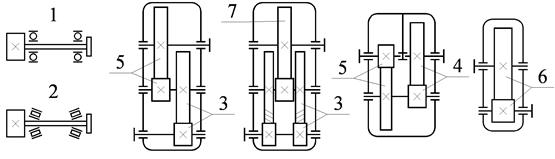
 выбирают по табл.2.7 в зависимости от положения зубчатых колес относительно опор.
выбирают по табл.2.7 в зависимости от положения зубчатых колес относительно опор.
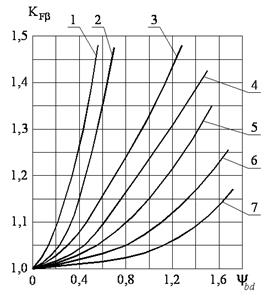
 при
при 


 ,
,  учитывающие распределение нагрузки между зубьями в связи с погрешностями изготовления шестерни и колеса, определяют по следующим приближенным зависимостям:
учитывающие распределение нагрузки между зубьями в связи с погрешностями изготовления шестерни и колеса, определяют по следующим приближенным зависимостям: ,
, 
 ,
, 
 – число, обозначающее степень точности по нормам плавности (ГОСТ 1643-81) (
– число, обозначающее степень точности по нормам плавности (ГОСТ 1643-81) ( .
.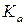 = 410 для косозубых и шевронных зубчатых колес и
= 410 для косозубых и шевронных зубчатых колес и  выбирают в соответствии с рекомендациями п. 2.10.
выбирают в соответствии с рекомендациями п. 2.10. округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra40. При проектировании крупносерийных редукторов
округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra40. При проектировании крупносерийных редукторов  .
.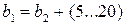 . Полученные значения
. Полученные значения  и
и  округляют до ближайших больших целых значений в миллиметрах.
округляют до ближайших больших целых значений в миллиметрах. ;
;  .
. выбирают из табл. 2.8 или назначают исходя из конкретных конструктивных, технологических или экономических требований. Следует учитывать, что с уменьшением коэффициента
выбирают из табл. 2.8 или назначают исходя из конкретных конструктивных, технологических или экономических требований. Следует учитывать, что с уменьшением коэффициента  увеличивается модуль и это приводит к повышению изгибной прочности зубьев. Кроме того, с увеличением модуля передача становится менее чувствительной к колебанию межосевого расстояния, вызванного неточностью изготовления и упругими деформациями валов и опор. Однако увеличение модуля уменьшает плавность работы передачи, увеличивает диаметр заготовки и машинное время при нарезании зубьев.
увеличивается модуль и это приводит к повышению изгибной прочности зубьев. Кроме того, с увеличением модуля передача становится менее чувствительной к колебанию межосевого расстояния, вызванного неточностью изготовления и упругими деформациями валов и опор. Однако увеличение модуля уменьшает плавность работы передачи, увеличивает диаметр заготовки и машинное время при нарезании зубьев. ,
не более
,
не более
 определяют из условия изгибной прочности колеса по следующей зависимости:
определяют из условия изгибной прочности колеса по следующей зависимости: ,
, – коэффициент, равный 3400 для прямозубых передач и 2800 для косозубых передач;
– коэффициент, равный 3400 для прямозубых передач и 2800 для косозубых передач; определяют в п. 2.10.
определяют в п. 2.10. определяют из условия неподрезания зубьев у основания:
определяют из условия неподрезания зубьев у основания: .
.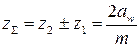 .
. должно быть целым числом, иногда приходится изменять значения
должно быть целым числом, иногда приходится изменять значения  .
. = 25°.
= 25°.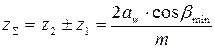 .
.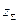 округляют в меньшую сторону до целого числа и определяют действительное значение угла (точность вычислений 0,0001):
округляют в меньшую сторону до целого числа и определяют действительное значение угла (точность вычислений 0,0001): ,
,  .
. и колеса
и колеса  :
:
 =
= 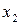 =0),
=0),  = 17 и
= 17 и  соответственно.
соответственно. ,
,  .
. .
. ;
; ;
; ;
;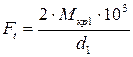 ,
, ,
, ,
, ,
, 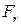 и
и  – окружная, радиальная и осевая сила соответственно.
– окружная, радиальная и осевая сила соответственно.


