
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка прочности зубьев по напряжениям изгибаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчёт выполняют отдельно для шестерни и для зубчатого колеса передачи после уточнения нагрузок на зубчатые колёса и их геометрических параметров. Проверяют справедливость соотношения расчётных напряжений изгиба − для прямозубых колёс − для косозубых колёс где Окружное усилие в зацеплении колёс рассчитывают по формуле Коэффициент неравномерности распределения нагрузки по длине линии контакта Коэффициент формы зуба YF для прямозубых колёс назначают по табл. 2.9 в зависимости от фактического числа зубьев для прямозубых колёс и от числа зубьев эквивалентных колёс Если при проверочном расчёте рабочие напряжения изгиба
Таблица 2.9. Коэффициент формы зуба YF
Расчёт открытой цилиндрической зубчатой передачи Учитывая условия и характер работы открытых передач (недостаточная защищённость от загрязнения абразивными частицами и увеличенный абразивный износ при плохой смазке, большие деформации валов, что приводит к увеличению зазоров в зацеплении, возрастанию динамических нагрузок, к понижению прочности изношенных зубьев вследствие уменьшения площади их поперечного сечения и, как следствие, к поломке зубьев), данные передачи рекомендуют рассчитывать по напряжениям изгиба. В этих передачах выкрашивание не наблюдается, так как поверхностные слои зубьев изнашиваются и удаляются раньше, чем появляются усталостные трещины. Для проектного расчёта открытых передач по напряжениям изгиба определяют модуль зацепления из выражений: − для прямозубых колес − для косозубых колес Здесь: z 3 − число зубьев шестерни открытой передачи (см. исходные данные);
Т 3 − момент на шестерне, Нм;
YF 3 − смотри табл. 2.9. Полученное значение модуля округляют в большую сторону до значения из стандартного ряда модулей (см. п. 2.5). Зная значение модуля, определяют геометрические размеры шестерни: диаметр делительный − диаметр вершин зубьев − диаметр впадин зубьев − ширина венца − Точность вычисления диаметров шестерни до 0,001 мм, значение ширины зубчатого венца округляют до целого числа по нормальным линейным размерам (см. табл. 2.5). Проверочный расчет такой передачи по контактным напряжениям выполняют в соответствии с п. 2.6. («Проверочный расчет закрытой цилиндрической передачи»). Расчёт закрытой конической зубчатой передачи Наибольшее применение в редукторостроении получили прямозубые конические колёса, у которых оси валов пересекаются под углом
Рис. 2.4
Проектный расчёт Основной габаритный размер передачи − делительный диаметр колеса по внешнему торцу − рассчитывают по формуле: где Е пр − приведённый модуль упругости, для стальных колёс T 2 − вращающий момент на валу колеса, Нмм (см.п.2.4);
Здесь Кbe − коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, Кbe = bw / Re. Рекомендуют принять
Рис. 2.5
Наиболее распространено в редукторостроении значение Кbe = 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид где u p– расчетное передаточное число конической передачи,
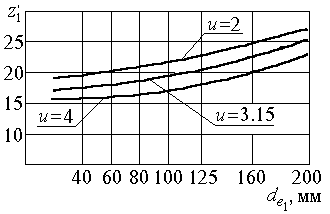
Геометрический расчёт Определяют делительный диаметр шестерни по внешнему торцу Число зубьев шестерни По значению Вычисленное значение z 1 округляют до целого числа.
Рис. 2.6
Определяют число зубьев колеса Вычисленное значение - передаточное число передачи - угол делительного конуса колеса - угол делительного конуса шестерни - внешний окружной модуль Рекомендуется округлить me до стандартного значения me ф по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров Рассчитывают величину внешнего конусного расстояния передачи (рис. 2.4) Рабочая ширина зубчатого венца колеса определяют как Полученное значение Определяют расчётный модуль зацепления в среднем сечении зуба При этом найденное значение mm не округляют! Рассчитывают внешнюю высоту головки зуба Внешнюю высоту ножки зуба определяют как Внешний диаметр вершин зубьев колёс рассчитывают по формуле Угол ножки зуба рассчитывают по формуле
Проверочный расчёт При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия где E пр − приведённый модуль упругости, для стальных колёс здесь Далее проверяют зубья колёс на выносливость по напряжениям изгиба по формулам: где
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |

 и допускаемых напряжений
и допускаемых напряжений  :
: ;
; ,
, − коэффициент повышения прочности косозубых передач по напряжениям изгиба,
− коэффициент повышения прочности косозубых передач по напряжениям изгиба,  . Здесь
. Здесь  − коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии на зубе к основанию зуба,
− коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии на зубе к основанию зуба,  , где
, где  подставляют в градусах. Коэффициент неравномерности распределения нагрузки между одновременно зацепляющимися зубьями KF назначают по табл. 2.8.
подставляют в градусах. Коэффициент неравномерности распределения нагрузки между одновременно зацепляющимися зубьями KF назначают по табл. 2.8. , Н.
, Н.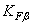 определяют по графикам рис. 2.3 а, б, аналогично рассмотренному выше определению значения коэффициента
определяют по графикам рис. 2.3 а, б, аналогично рассмотренному выше определению значения коэффициента  .
. − для косозубых колес. Табл. 2.9 составлена для случая отсутствия смещения зуборезного инструмента (x = 0) при зубонарезании.
− для косозубых колес. Табл. 2.9 составлена для случая отсутствия смещения зуборезного инструмента (x = 0) при зубонарезании. в зубьях колёс оказываются значительно меньшей величины, чем допускаемые напряжения
в зубьях колёс оказываются значительно меньшей величины, чем допускаемые напряжения  , то для закрытых передач это вполне допустимо, так как нагрузочная способность таких передач ограничивается, как правило, контактной выносливостью зубьев.
, то для закрытых передач это вполне допустимо, так как нагрузочная способность таких передач ограничивается, как правило, контактной выносливостью зубьев.

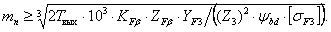
 − коэффициент ширины зубчатого венца колеса относительно начального диаметра шестерни, рекомендуют назначать для открытых передач
− коэффициент ширины зубчатого венца колеса относительно начального диаметра шестерни, рекомендуют назначать для открытых передач 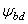 = 0,1…2,0;
= 0,1…2,0; − допускаемое напряжение изгиба зубьев шестерни, Н/мм2, определяют в соответствии с п. 2.3. («Расчет допускаемых напряжений»);
− допускаемое напряжение изгиба зубьев шестерни, Н/мм2, определяют в соответствии с п. 2.3. («Расчет допускаемых напряжений»);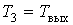 ;
; − смотри выше, для проектного расчета принять
− смотри выше, для проектного расчета принять  или
или 



 (рис. 2.4), так называемые ортогональные передачи.
(рис. 2.4), так называемые ортогональные передачи.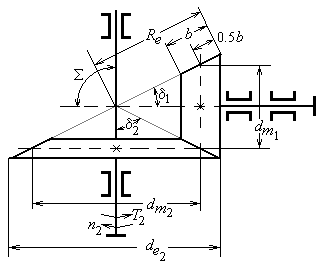
 ,
, МПа;
МПа; . Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H 1 и H 2 > 350 HB или V > 15 м/с.
. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H 1 и H 2 > 350 HB или V > 15 м/с.
 ,
, или up = z 2 / z 1.
или up = z 2 / z 1. .
. назначают по рекомендациям, представленным на рис. 2.6.
назначают по рекомендациям, представленным на рис. 2.6. при Н 1 и
при Н 1 и  ,
,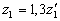 при
при 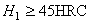 и
и  при Н 1 и
при Н 1 и  .
.
 .
. округляют до целого числа. После этого необходимо уточнить:
округляют до целого числа. После этого необходимо уточнить: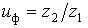 ,
, ,
, ,
, .
.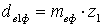 и
и  .
. .
. .
. округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5).
округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5). .
. .
. .
. .
. .
.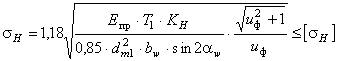 ,
, − вращающий момент на шестерне, Нмм,
− вращающий момент на шестерне, Нмм,  ;
; − КПД передачи.
− КПД передачи.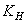 − коэффициент расчётной нагрузки,
− коэффициент расчётной нагрузки,  ; коэффициент концентрации нагрузки
; коэффициент концентрации нагрузки 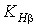 найден ранее по графикам рис. 2.5.
найден ранее по графикам рис. 2.5.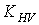 − коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости
− коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости  в соответствии с рекомендациями (табл. 2.6);
в соответствии с рекомендациями (табл. 2.6); − делительный диаметр шестерни в среднем сечении зуба,
− делительный диаметр шестерни в среднем сечении зуба,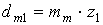 ;
; − угол зацепления,
− угол зацепления,  и
и 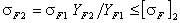 ,
,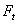 − окружное усилие в зацеплении, Н,
− окружное усилие в зацеплении, Н,  ;
;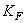 − коэффициент расчётной нагрузки,
− коэффициент расчётной нагрузки,  . Здесь
. Здесь 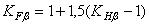 , а
, а 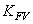 определяют по табл. 2.7 с понижением точности на одну степень против фактической.
определяют по табл. 2.7 с понижением точности на одну степень против фактической. − коэффициент формы зуба соответственно шестерни и колеса, находят по табл. 2.9 в зависимости от эквивалентного числа зубьев колёс
− коэффициент формы зуба соответственно шестерни и колеса, находят по табл. 2.9 в зависимости от эквивалентного числа зубьев колёс .
.


