Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет прочности зубьев по напряжениям изгибаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчет прочности зубьев по напряжениям изгиба носит проверочный характер
где
где
Проведем расчет для передачи I.
Принимаем
Проведем расчет для передачи II.
Принимаем Таким образом, полученные размеры колес и шестерней удовлетворяют всем проверкам. Объединим все полученные данные в таблицу
Таблица 6 Параметры зубчатой передачи
Расчет вала
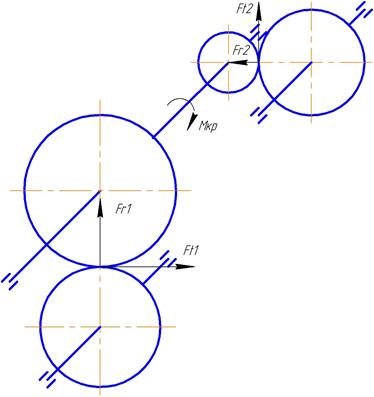
Определение сил в зацеплении
Так как в данном задании прямозубое зацепление, осевая сила равна нулю. Нормальная сила направлена по линии зацепления к рабочим поверхностям зубьев. При этом нормальная сила раскладывается на окружную и радиальную силы, которые вычисляются по следующим формулам:
где Мкр – крутящий момент; d – диаметр зубчатого колеса.
Для передачи I.
По формуле (21) определяем окружную силу: Из формулы (22) радиальная сила равна:
Для передачи II.
Вычисляем по формуле (21) окружную силу:
Определение длины вала
Определяем расстояния между опорами и зацеплениями: Согласно таблице 1:
Общая длина вала L=
Выбор расчетной схемы и определение расчетных нагрузок Составляем расчетную схему промежуточного вала (рис. 11.) Определяем реакции опор. Вычисляем и строим эпюры изгибающих, крутящего и приведенного моментов. Эпюра моментов – это график, который показывает, как меняется момент по длине вала. Вал можно представить как балку на двух опорах, нагруженную силами в двух плоскостях. Следовательно, необходимо рассмотреть вал отдельно плоскостях XOY и XOZ.
Рис. 11 Расчетная схема вала
Рис. 12 Схема действия сил
Рассмотрим силы, действующие в плоскости XOY (Рис 12.). Рассмотрим проекцию на горизонтальную плоскость. Определяем реакции опор, которые находятся из условия равенства моментов. Запишем сумму моментов относительно точки А:
Запишем сумму моментов относительно точки В:
Проверка делается по условию равенства проекций:
Рассмотрим силы, действующие в плоскости XOZ (рис 12.). Запишем сумму моментов относительно точки А:
Запишем сумму моментов относительно точки В:
Проверка:
Считаем суммарные реакции RA, RB и HA:
Таблица 7 Силы в зацеплении
Построение эпюр моментов Эпюры изгибающих моментов
Так как силы действуют на вал в двух плоскостях, следовательно, эпюры необходимо также строить в двух плоскостях XOY и XOZ. Рассмотрим силы, действующие в плоскости XOZ(см. рис.12). Напишем сумму моментов для 1-го участка:
М(0)=0; М( Сумма моментов для 2-го участка:
М(0)= Сумма моментов для 3-го участка:
М(0)= М(
Построим эпюру изгибающих моментов в вертикальной плоскости:
Рис.13 Эпюра изгибающих моментов в вертикальной плоскости
Рассмотрим силы, действующие в плоскости XOY(см.рис.12). Напишем сумму моментов для 1-го участка:
М(0)=0; М( Сумма моментов для 2-го участка:
М(0)= Сумма моментов для 3-го участка:
М( М(0)= Построим эпюру изгибающих моментов в горизонтальной плоскости:
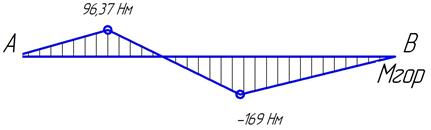
Рис.14 Эпюра изгибающих моментов в горизонтальной плоскости Эпюра крутящих моментов
Крутящий момент передается валу колесом и снимается шестерней, но моменты на них одинаковы, следовательно, эпюра крутящего момента будет выглядеть следующим образом:
Рис.15 Эпюра крутящих моментов
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.009 с.) |

 , (19)
, (19) - коэффициент формы зуба, который принимается в зависимости от суммарного количества зубьев на колесе и шестерни;
- коэффициент формы зуба, который принимается в зависимости от суммарного количества зубьев на колесе и шестерни;  - коэффициент концентрации нагрузки при расчетах по напряжениям изгиба причем,
- коэффициент концентрации нагрузки при расчетах по напряжениям изгиба причем, 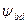 );
);  [1] (для передач без смещения, x∑=0);
[1] (для передач без смещения, x∑=0);  - коэффициент расчетной нагрузки при расчетах по напряжениям изгиба.
- коэффициент расчетной нагрузки при расчетах по напряжениям изгиба. , (20)
, (20)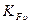 - коэффициент динамической нагрузки при расчетах по напряжениям изгиба.
- коэффициент динамической нагрузки при расчетах по напряжениям изгиба. , тогда по формуле (19):
, тогда по формуле (19): 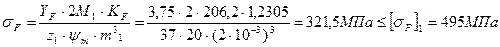 .
. , тогда по формуле (19):
, тогда по формуле (19):  .
. ,
мм
,
мм

 ,
мм
,
мм
 , мм
, мм
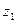
 ; (21)
; (21) , (22)
, (22) Н
Н .
.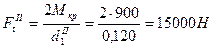 , из формулы (22) радиальная сила равна:
, из формулы (22) радиальная сила равна:  .
.
 =74,8+48+88,4=211,2 мм.
=74,8+48+88,4=211,2 мм.


 .
.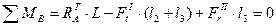
 ;
;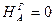 Н.
Н.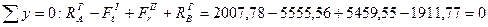 Н.
Н.
 .
.
 ;
; Н.
Н. Н.
Н. ;
; ;
;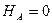 .
. , Н
, Н
 , Н
, Н
 , Н
, Н
 , Н
, Н
 , где 0 £х£
, где 0 £х£ 
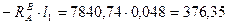 Нм
Нм , где 0 £х£
, где 0 £х£ 
 Нм; М(
Нм; М( Нм
Нм , где 0 £х£
, где 0 £х£ 
 Нм;
Нм; =811,6Нм
=811,6Нм
 , где 0 £х£
, где 0 £х£  H м.
H м. , где 0 £х£
, где 0 £х£ 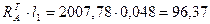 Н м; М(
Н м; М( Н м.
Н м. , где 0
, где 0  х
х 
 Н м.
Н м. Н м;
Н м;