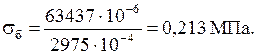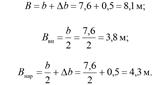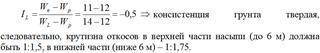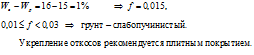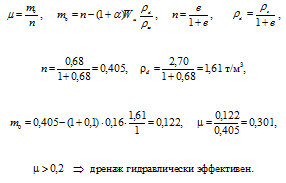Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчеты пути на прочность и устойчивостьСодержание книги
Поиск на нашем сайте
3.7 Определить среднюю величину, среднее квадратическое отклонение и максимально вероятную величину расчетной нагрузки от колеса на рельс, если статическая нагрузка от веса экипажа на колесо Pст = 100000 Н, а среднее значение силы инерции от колебания кузова на рессорах
3.7 Определить среднюю величину, среднее квадратическое отклонение и максимально вероятную величину расчетной нагрузки от колеса на рельс, если статическая нагрузка от веса экипажа на колесо Pст = 143139 Н, а среднее значение силы инерции от колебания кузова на рессорах
Решение задачи Среднее значение расчетной нагрузки от колеса на рельс определяется по формуле
Здесь P ст – статическая нагрузка колеса на рельс;
Расчетная нагрузка определяется по формуле
Численные значения P расч и S расч составят
3.8 Определить эквивалентную нагрузку Определить эквивалентную нагрузку
Решение задачи Определим вначале P расч по формуле
Максимальная эквивалентная нагрузка для расчета изгибных напряжений в рельсах определяется по формуле
где
Расчет ведется для системы, состоящей из трех колесных нагрузок. Для этого случая координаты средних нагрузок равны x 1 = l 1, x 2 = l 1 + l 2. Причем для двухосной тележки l 2 –– это расстояние между крайней осью первой тележки и первой осью следующей по ходу поезда тележки. Значения расстояний l 1 и l 2 для четырехосного грузового вагона x 1 = l 1 = 1,85 м; x 2 = l 1 + l 2 = 1,85 + 6,75 = 8,6 м. Ординаты линии влияния изгибающих моментов рельса
Максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба определяется по формуле
3.9 Определить эквивалентную нагрузку
Определить эквивалентную нагрузку
Решение задачи Максимальная величина эквивалентной нагрузки определяется по формуле
где
В этом случае при расчете Определим вначале P расч по формуле
Ординаты линии влияния давления рельса на шпалу определяются следующим образом
Максимальная величина эквивалентной нагрузки для определения давления рельса на шпалу:
3.10 Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк при воздействии эквивалентной нагрузки
Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк при воздействии эквивалентной нагрузки
Решение задачи Нормальные изгибные напряжения в подошве рельса находятся по общеизвестной формуле
где М – изгибающий момент; W п – момент сопротивления относительно наиболее удаленного волокна. Напряжения в кромке подошвы рельса
Здесь: f – коэффициент, переводящий осевые напряжения в подошве в кромочные напряжения; он учитывает влияние горизонтальных поперечных сил Н и внецентренное приложение вертикальных сил Р. Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
Осевые изгибные напряжения в подошве рельса
Изгибные напряжения в кромке подошвы рельса
3.11 Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина расчетной нагрузки P расч = 158000 Н, средняя величина расчетной нагрузки
Определить напряжения изгиба в подошве рельса: осевые σпо и кромочные σпк от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина расчетной нагрузки P расч = 182946 Н, средняя величина расчетной нагрузки
Решение задачи Нормальные изгибные напряжения в подошве рельса находятся по общеизвестной формуле
где М – изгибающий момент; W п – момент сопротивления относительно наиболее удаленного волокна. Напряжения в кромке подошвы рельса
Здесь: f – коэффициент, переводящий осевые напряжения в подошве в кромочные напряжения; он учитывает влияние горизонтальных поперечных сил Н и внецентренное приложение вертикальных сил Р. Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
Максимальная эквивалентная нагрузка для расчета изгибных напряжений в рельсах определяется по формуле
где
Для заданных условий координаты средних нагрузок равны x 1 = l 1, x 2 = l 1 + l 2. Причем для двухосной тележки l 2 – это расстояние между крайней осью первой тележки и первой осью следующей по ходу поезда тележки. Значения расстояний l 1 и l 2 для четырехосного грузового вагона x 1 = l 1 = 1,85 м; x 2 = l 1 + l 2 = 1,85 + 6,75 = 8,6 м. Ординаты линии влияния изгибающих моментов рельса
Максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба определяется
Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
Осевые изгибные напряжения в подошве рельса
Изгибные напряжения в кромке подошвы рельса
3.12 Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если средняя величина расчетной нагрузки
Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если средняя величина расчетной нагрузки
Решение задачи В начале определим расчетную нагрузку от колеса на рельс
Для заданных условий
Напряжения смятия в деревянных шпалах под подкладками и в прокладках при железобетонных шпалах определяются по формуле
где Q – давление колеса на рельс; w – площадь передачи давления на шпалу через подкладку или прокладку (при бесподкладочном скреплении типа ЖБР). Напряжения в балластном слое под шпалой в подрельсовом сечении определяется по формуле
где 0,5 аb – площадь полушпалы (а и b – длина и ширина шпалы); α – коэффициент изгиба шпалы; Ωα – эффективная площадь полушпалы с учетом изгиба. Давление колеса на рельс определяется по формуле
Максимальная величина эквивалентной нагрузки определяется по формуле
где
При расчете Подставив численные значения в приведенные здесь формулы, определим напряжения в элементах верхнего строения пути.
3.13 Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина эквивалентной нагрузки
Определить напряжения сжатия в резиновых прокладках на шпалах σш и в балластном слое под шпалой σб от воздействия колес двухосной тележки с расстоянием между осями l = 1,85 м, если величина эквивалентной нагрузки
Решение задачи Напряжения смятия в деревянных шпалах под подкладками и в прокладках при железобетонных шпалах определяются по формуле
где Q – давление колеса на рельс; w – площадь передачи давления на шпалу через подкладку или прокладку (при бесподкладочном скреплении типа ЖБР). Напряжения в балластном слое под шпалой в подрельсовом сечении определяется по формуле
где 0,5 аb – площадь полушпалы (а и b – длина и ширина шпалы); α – коэффициент изгиба шпалы; Ωα – эффективная площадь полушпалы с учетом изгиба. Давление колеса на рельс определяется по формуле
Подставив численные значения в приведенные здесь формулы, определим напряжения в элементах верхнего строения пути.
3.14 Поезд движется по спуску крутизной i = 7 ‰ и по кривой R = 400 м, основное сопротивление движению вагонов ω ’’ 0 = 1,7 Н/кН. Определить суммарное сопротивление движению вагонов.
Поезд движется по спуску крутизной i = 5 ‰ и по кривой R = 500 м, основное сопротивление движению вагонов ω ’’ 0 = 1,7 Н/кН. Определить суммарное сопротивление движению вагонов.
Решение задачи Суммарное удельное сопротивление движению вагонов в поезде определяется по формуле
Здесь Суммарное удельное сопротивление
3.15 Определить поперечную составляющую продольной силы в поезде, действующую наружу кривой R = 500 м, если величина продольной силы в автосцепке N = 700 кН.
Определить поперечную составляющую продольной силы в поезде, действующую наружу кривой R = 600 м, если величина продольной силы в автосцепке N = 600 кН.
Решение задачи Поперечная составляющая продольной силы в поезде Δ H определяется по формуле
3.16 Определить устойчивость колеса на рельсе в кривой при величине нагрузок от колес на рельсы P = 105 кН, величине рамной силы Ур = 85 кН и величине непогашенного поперечного ускорения αн = 0,25 м/с2.
Определить устойчивость колеса на рельсе в кривой при величине нагрузок от колес на рельсы P = 110 кН, величине рамной силы Ур = 80 кН и величине непогашенного поперечного ускорения αн = 0,3 м/с2.
Решение задачи Коэффициент запаса устойчивости колеса на рельсе определяется по формуле
Нагрузки на наружный и внутренний рельсы кривой определяются по формулам
где Q – вес вагона, приходящийся на одну ходовую тележку Q = 4 P = 4·110 = 440 кН. Тогда
Проверка (126,76+93,24)/2=110 кН. Подставив полученные значения в первую формулу, получим
В заданных условиях колесо устойчиво на рельсе.
Расчеты бесстыкового пути
3.17 Определить длину концевого участка продольных деформаций рельсовых плетей Р65 при температуре рельсов минус 40 °С и температуре закрепления +25 °С (при нормативной затяжке гаек клеммных и закладных болтов). Стыковое сопротивление 300 кН. Нарисовать эпюру продольных сил. 3.18 Определить величину раскрытия зазора при изломе рельсовой плети Р65 при температуре рельсов –45 °С и температуре закрепления +35 °С (при нормативной затяжке гаек клеммных и закладных болтов). Построить эпюру продольных сил. 3.19 Определить температурную силу при температуре рельсовой плети Р65 минус 25 °С, температуре закрепления + 35 °С на участке плети между «маячными» шпалами при сдвиге плети относительно «маячных» шпал в начале участка на минус 10 мм, в конце на 5 мм. 3.20 Определить границы интервала закрепления бесстыковой плети при наибольшей температуре рельсов в данной местности tmaxmax = +58 °С, наименьшей tminmin = –54 °С, допускаемое повышение [Δtу] = 45 °С и понижение [Δtр] = 95 °С температуры рельсов.
Расчеты земляного полотна
3.21 Определить ширину основной площадки земляного полотна B и начертить ее схему, для однопутного участка I категории железнодорожной линии в кривой радиусом R = 500 м, грунт земляного полотна – пылеватый песок.
Ширина основной площадки b на прямых однопутных участках, м
Уширение основной площадки D b на кривых участках, м
Схема основной площадки земляного полотна
3.22 Назначить крутизну откосов и начертить схему поперечного профиля для насыпи высотой 11 м на однопутном участке, сооружаемой из глинистого грунта со следующими характеристиками: влажность на границе раскатывания Wp = 12 %, влажность на границе текучести WL = 14 %, природная влажность We = 11 %.
Крутизна откосов насыпей
Схема поперечного профиля насыпи
3.23 Определить интенсивность пучения грунта f при следующих значениях влажности грунта: We = 16 %, Wp = 15 %. Рекомендовать способ защиты откосов земляного полотна и определить отметку бермы Гб при следующих исходных данных: ГВВ = 198,4 м, hп = 0,2 м, hн = 1,1 м, D Z = 0,15 м.
Интенсивность пучения f глинистых грунтов в зависимости от влажности в зоне промерзания
Схема к расчету отметки бермы Гб
3.24 Оценить гидравлическую эффективность дренажа, устраиваемого на участке выемки, сложенной грунтами, имеющими условный номер 7в.
Физико-технические характеристики грунта
3.25 Изобразить типовой поперечный профиль щебеночной балластной призмы в кривой на однопутном участке для 1 класса пути. Представить схему с указанием основных размеров. Типовой поперечный профиль балластной призмы
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1083; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 = 16800 Н, среднее квадратическое отклонение нагрузки от колебания надрессорного строения Sр = 1800 Н, от сил инерции необрессоренных масс, вызванных: неровностью на пути Sнп = 9200 Н, изолированной неровностью на колесе Sинк = 15000 Н, непрерывной неровностью на колесе Sннк = 2000 Н.
= 16800 Н, среднее квадратическое отклонение нагрузки от колебания надрессорного строения Sр = 1800 Н, от сил инерции необрессоренных масс, вызванных: неровностью на пути Sнп = 9200 Н, изолированной неровностью на колесе Sинк = 15000 Н, непрерывной неровностью на колесе Sннк = 2000 Н. = 15592 Н, среднее квадратическое отклонение нагрузки от колебания надрессорного строения Sр = 3598 Н, от сил инерции необрессоренных масс, вызванных: неровностью на пути Sнп = 8209 Н, изолированной неровностью на колесе Sинк = 15363 Н, непрерывной неровностью на колесе Sннк = 1330 Н.
= 15592 Н, среднее квадратическое отклонение нагрузки от колебания надрессорного строения Sр = 3598 Н, от сил инерции необрессоренных масс, вызванных: неровностью на пути Sнп = 8209 Н, изолированной неровностью на колесе Sинк = 15363 Н, непрерывной неровностью на колесе Sннк = 1330 Н.
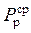 – среднее значение динамической добавки от колебания кузова на рессорах.
– среднее значение динамической добавки от колебания кузова на рессорах.
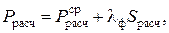
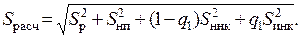


 от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения изгибающего момента при средней величине расчетной нагрузки
от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения изгибающего момента при средней величине расчетной нагрузки  = 122000 Н, величине среднего квадратического отклонение расчетной нагрузки
= 122000 Н, величине среднего квадратического отклонение расчетной нагрузки  = 14500 Н и коэффициента относительной жесткости подрельсового основания и рельса k = 1,421 м-1.
= 14500 Н и коэффициента относительной жесткости подрельсового основания и рельса k = 1,421 м-1. от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения изгибающего момента при средней величине расчетной нагрузки
от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения изгибающего момента при средней величине расчетной нагрузки 


 – ординаты линии влияния изгибающих моментов рельса в сечениях пути xi, расположенных под колесными нагрузками тележки
– ординаты линии влияния изгибающих моментов рельса в сечениях пути xi, расположенных под колесными нагрузками тележки  на расстоянии xi от, смежных с расчетной осью
на расстоянии xi от, смежных с расчетной осью


 от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения прогиба рельса и нагрузки рельса на шпалу при средней величине расчетной нагрузки
от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения прогиба рельса и нагрузки рельса на шпалу при средней величине расчетной нагрузки  от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения прогиба рельса и нагрузки рельса на шпалу при средней величине расчетной нагрузки
от колес двухосной тележки с расстояниями между осями l = 1,85 м на рельс для определения прогиба рельса и нагрузки рельса на шпалу при средней величине расчетной нагрузки 
 – ординаты линии влияния давлений рельса на шпалы в сечениях пути xi, расположенных под колесными нагрузками
– ординаты линии влияния давлений рельса на шпалы в сечениях пути xi, расположенных под колесными нагрузками  на расстоянии xi от осей тележки, смежных с расчетной осью
на расстоянии xi от осей тележки, смежных с расчетной осью
 координаты средних нагрузок
координаты средних нагрузок  равны x 1 = l 1, x 2 = l 2.
равны x 1 = l 1, x 2 = l 2.



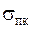 определяется по формуле
определяется по формуле




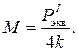

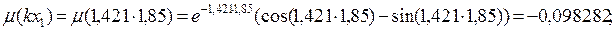

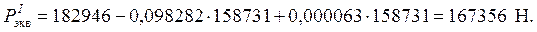


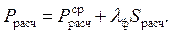



 координаты средних нагрузок
координаты средних нагрузок