Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Земляное полотно в сложных природных условияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 2.21 Определение требуемой плотности грунтов высоких насыпей.
Компрессионная кривая
1 – ветвь нагрузки; 2 – ветвь разгрузки
2.22 Расчет устойчивости откосов подтопляемой насыпи при круглоцилиндрической поверхности смещения.
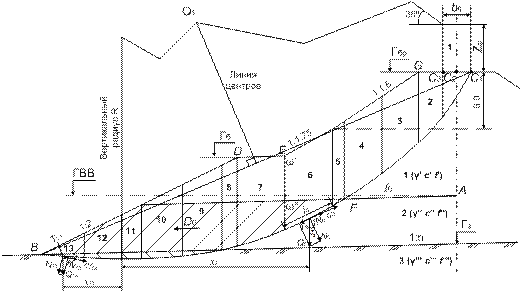
Расчетная схема к графоаналитическому расчету общей устойчивости подтопляемой насыпи
2.23 Расчет осадки основания земляного полотна, меры ограничения и компенсации осадок оснований.
2.24 Порядок проектирования горизонтальных гравитационных дренажей.
Расчетная схема двухстороннего (а) и одностороннего (б) подкюветного несовершенного дренажа
1 – граница промерзания; 2 – граница зоны капиллярного поднятия воды; 3 – поверхность депрессии; 4 – расчетное сечение; 5 – кровля водоупора
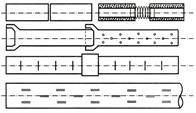
Конструкции дренажных труб
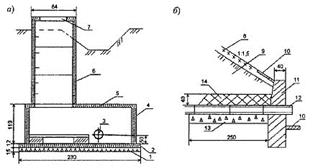
Смотровой колодец (а) и выпуск дренажа (б)
1 – подготовка из щебня; 2 – плита днища; 3 – дренажная труба; 4 – кольцо-камера; 5 – плита перекрытия; 6 – кольцо стеновое; 7 – кольцо опорное; 8 – одерновка; 9 – местный грунт; 10 – бетонные плиты; 11 – подпорная стенка; 12 – концевые дрены; 13 – щебень; 14 – утеплитель
2.25 Проектирование теплоизоляционных покрытий для исключения пучинных деформаций.
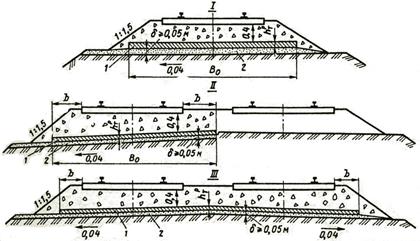
Схема устройства тепловой изоляции из пенополистирола
I – на однопутном участке; II – на двухпутном участке под один путь; III – на двухпутном участке под два пути; 1 – слой тепловой изоляции; 2 – дренирующая подушка
Расчеты пути на прочность и устойчивость 2.26 Виды воздействий на железнодорожный путь. Схема передачи вертикальной нагрузки от колеса на элементы пути. В целом элементы верхнего строения образуют единую конструкцию, непосредственно воспринимающую воздействие колес подвижного состава и передающую это воздействие на земляное полотно и искусственные сооружения. Работу верхнего строения, как единой конструкции, может характеризовать, например, схема передачи вертикальных нагрузок от колес подвижного состава на земляное полотно (рисунок).
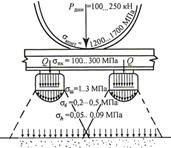
Схема передачи вертикальной нагрузки от колеса на основание пути: Р дин – вертикальная динамическая сила; σпк – напряжения в кромках подошвы рельса; σш – в шпале (в прокладке) под подкладкой; σб – в балласте под шпалой; σ h – на основной площадке земляного полотна Динамическая нагрузка от колеса передается на головку рельса по небольшой площадке. Площадь эллипса упругого контакта 1,2…2,2 см2. При внецентренном приложении нагрузки в кромках подошвы рельса возникают напряжения изгиба и кручения (100…300 МПа). Напряжения на шпале под металлической подкладкой бывают в пределах 1…3 МПа. Интенсивность давления шпалы на балласт составляет в среднем 0,2…0,3 МПа. Давление от шпал в балласте распространяется по мере углубления на все большую площадь, и на земляное полотно передается почти равномерное давление интенсивностью примерно 0,05…0,09 МПа. Таким образом, конструкция пути обладает распределяющей способностью. По мере удаления вниз от места непосредственного контакта колеса давление распространяется на все большую площадь, что позволяет применять для сооружения пути материалы с различными механическими характеристиками (сталь, дерево, искусственно уплотненные материалы балластного слоя, грунты земляного полотна и, наконец, грунты земной поверхности).
2.27 Основы статического расчета пути на прочность. Выбор расчетной схемы (модели). Связь между прогибом рельса и упругим отпором основания. Модуль упругости и коэффициент относительной жесткости рельсового основания. Под воздействием колес подвижного состава в элементах верхнего строения пути возникают напряжения и деформации. Величина их зависит от расчетной нагрузки, параметров пути и подвижного состава и расчетной модели их взаимодействия. В качестве расчетной схемы (модели) рельс рассматривается как балка бесконечной длины, постоянного сечения, лежащая на сплошном упругом основании (рисунок, а).
Расчетные схемы рельса как балки: а – на сплошном упругом основании; б – на прерывистом упругом основании; в – на упругих точечных опорах Фактически путь имеет упруго-прерывистое основание (рисунок, б). Замена такой фактической схемы на сплошное упругое основание определяет разницу в величинах напряжений в рельсах в 2–4 %. Можно рассматривать рельс как балку постоянного сечения на упругих поперечных опорах (рисунок, в). Разницы в величинах напряжений по сравнению с первой схемой 5–7%. Первая схема имеет достаточно простое аналитическое решение, удобна, дает простые расчетные формулы, достаточно точна, поэтому в настоящее время пользуются ею. Под действием силы Р рельс как балка на сплошном упругом основании изогнется следующим образом (рисунок).
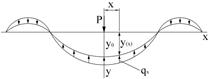
Изогнутая ось рельса под нагрузкой P и упругий отпор основания qx
Связь между прогибом yх в каждом сечении и погонным упругим отпором qх в том же сечении выражается зависимостью qх = – Uyх. Знак минус означает, что отпор направлен в сторону, противоположную направлению внешней силы (и прогибу). Связь между прогибом y и отпором q – линейная двухсторонняя; U – коэффициент пропорциональности, так называемый модуль упругости подрельсового основания.
2.28 Уравнение изогнутой оси рельса под колесной нагрузкой. Исследование его на нулевых и экстремальных значений. В результате решения уравнения четвертого порядка с постоянным коэффициентом, характеризующим поведение рельса, как балки на сплошном упругом основании, под воздействием колесной нагрузки P определим
Здесь U – модуль упругости подрельсового основания; k – коэффициент относительной жесткости подрельсового основания и рельса; y и x – ордината и абсцисса уравнения прогибов (изогнутой оси) рельса. В соответствии с приведенным уравнением (1) ординаты у пропорциональны значениям функции
Рассмотрим эпюру
Эпюра функции Нулевые значения этих величин определяются из условия h(kx) = 0 и m(kx) = 0, а относительные экстремумы – из условия В начале координат при х = 0 → h(kx) = m(kx) = 1. Первые максимумы: h(kx)min = – e -p » –0,0432 при х = p/ k; m(kx)mах = – e -p/2 » –0,208 при х = p/2 k. Вторые максимумы совсем незначительные: h(kx)max = 0,00187 и m(kx)min = 0,00898.
2.29 Воздействие на путь подвижного состава. Неровности пути и подвижного состава. Колебания необрессоренных масс подвижного состава. Вертикальные силы от колес к рельсам приложены статически. Но величина сил определяется с учетом динамики. Она складывается из статического давления колеса на рельс и динамических добавок, возникающих при колебаниях кузова и необрессоренных масс подвижного состава из-за наличия несовершенств пути и колес. В расчет принимается вероятное значение суммарной вертикальной силы:
Неровности на пути: 1) явные или геометрические. Их можно разделить на два вида: неровности продольного профиля пути, устанавливаемые нивелировкой по головке рельсов; микронеровности на поверхности катания головок рельсов, обусловленные волнообразным износом рельсов. Измеряются специальными приборами, имеющими прямолинейную базу, например, линейками; 2) неявные (потайные) или силовые, образующиеся из-за неплотного прилегания элементов верхнего строения пути друг к другу и выборки люфтов под нагрузкой (их можно обнаружить при медленном прокатывании колес по пути). Ординаты неровности на пути (ηп) представляют собой сумму ординат геометрических и силовых неровностей. При качении колеса по этим неровностям возникает вертикальная сила инерции P нп. Несовершенства колес: 1) несовпадение центра тяжести колеса с центром вращения, которое вызывает дисбаланс. Дисбаланс может иметь место из-за: неравномерного распределения металла по сечению колеса; эксцентричной насадки колеса на ось (допускается эксцентричность до 1 мм); 2) неравномерности проката (износа) колеса по среднему кругу катания (овальность, ползун). Все это вызывает дополнительные силы инерции, обусловленные несовершенством колес (неровностями ηк на колесах). Вертикальная составляющая этих сил P нк является знакопеременной. Таким образом, путь и колеса обладают различными несовершенствами в виде неровностей явных (геометрических) или неявных (силовых). Кроме того, все неровности можно разделить на два характерных вида: ‒ изолированные (их влияние на величину сил инерции заканчивается до следующей неровности); ‒ непрерывные (непосредственно примыкают друг к другу).
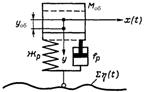
2.30 Колебания обрессоренных масс подвижного состава. Выражение, описывающее максимальный прогиб рессор. При наличии неровностей на пути и на колесах последние при поступательном движении по этим неровностям то поднимаются, то опускаются и увлекают за собой рессорные комплекты, вызывая их колебания и находящихся на них обрессоренных масс. Колеблющаяся обрессоренная масса создает силы инерции, равные произведению массы на действующее на нее ускорение. Обозначим M об – обрессоренную массу, приходящуюся на одно колесо, у р – ординату колебания этой массы на рессоре (на рессорном комплекте) относительно своего статического положения. Сила инерции этой массы I об = M об у р. Сила инерции колеблющейся на рессоре массы возбуждает равную ей по значению и обратную по знаку реакцию рессоры Р р. При незатухающих колебаниях эта реакция пропорциональна деформации (сжатия, разжатия) рессоры, равной уже ранее указанному значению у р и обратной ей по знаку. Таким образом
Расчетная модель колебаний обрессоренных масс: М об – обрессоренная масса (кузова) – представляется в виде единой сосредоточенной массы, приведенной к колесу; Жр – жесткость рессорного подвешивания, приведенная к колесу; f р – коэффициент вязкого трения в рессорном комплекте; ∑η(t) – суммарная неровность пути и колеса В отличие от колебаний необрессоренных масс, колебания кузова не имеют синусоидального характера, они более сложны и неопределенны. Поэтому на основании обширного эмпирического материала принято определять максимальную силу инерции, возникающую от колебаний кузова на рессорах, как
где у p-max – максимальное сжатие рессор при движении экипажа по всей совокупности неровностей:
Это уравнение эмпирическое. Коэффициенты а р и b p найдены для каждой единицы подвижного состава экспериментально. Для новых локомотивов, в том числе с повышенными осевыми нагрузками, Р р-max определяется через коэффициент вертикальной динамики обрессоренных масс k д0.
где Р ст – статическая нагрузка на колесо; q к – вес необрессоренных масс, приходящийся на одно колесо. Величина k д0 зависит от типа экипажа и скорости движения и определяется экспериментально (обычно kд0 ≈ 0,2 + 0,4).
2.31 Определение расчетной нагрузки от колеса на рельс. Составляющие вертикальной динамической силы. Расчетная нагрузка является динамической максимально вероятной величиной
Здесь
Учитываются следующие слагаемые вероятностной силы P:
где
Средние значения сил Поэтому среднее значение расчетной нагрузки
Детерминированная статическая нагрузка
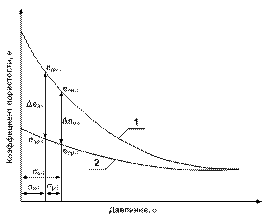
где Q – вес экипажа; n – число колес. Среднее квадратическое отклонение расчетной нагрузки колеса на рельс S расч определяется по формуле композиции законов распределения его составляющих
где S р – среднее квадратическое отклонение расчетной нагрузки колеса на рельс от вертикальных колебаний надрессорного строения; S нп – среднее квадратическое отклонение расчетной нагрузки колеса на рельс от сил инерции необрессоренных масс при прохождении колесом изолированной неровности пути; S ннк – среднее квадратическое отклонение расчетной нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за непрерывной неровности на поверхности катания колеса; S инк – среднее квадратическое отклонение расчетной нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за наличия на поверхности катания колеса плавной изолированной неровности; q 1 – доля колес, имеющих изолированные неровности, q 1 = 0,05.
2.32 Определение эквивалентных нагрузок от колес на рельс. При расчете рельса как балки на сплошном упругом основании система сосредоточенных колесных нагрузок заменяется эквивалентными одиночными нагрузками, соответственно при определении изгибающих моментов и напряжений в рельсах с помощью функции μ(kx) и при определении нагрузок и прогибов с помощью функции η(kx). Поскольку в силу случайной природы вероятный максимуму динамической нагрузки расчетного колеса не совпадает с вероятным максимумом нагрузок соседних колес, то при определении эквивалентных нагрузок принимается максимальная вероятная нагрузка расчетного колес и среднее значение нагрузок соседних колес.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |


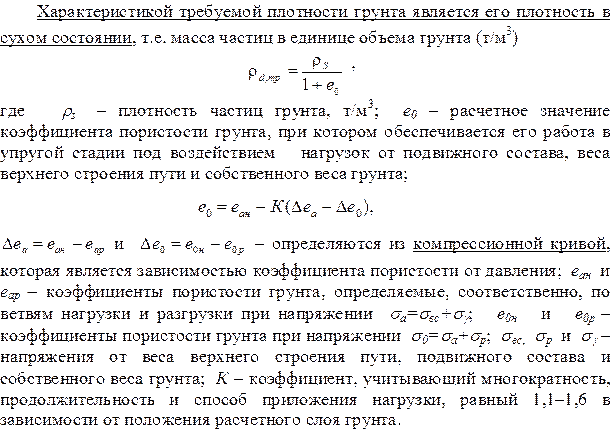





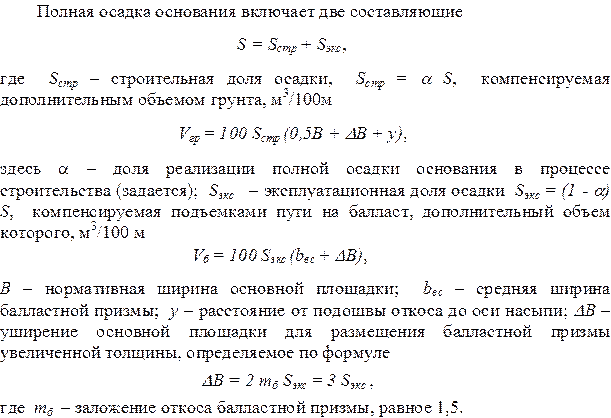










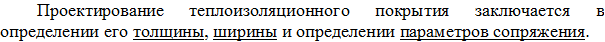



 (1)
(1)
 при P = 1
при P = 1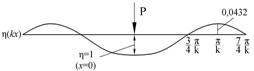
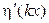 = 0 и
= 0 и 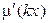 = 0.
= 0.
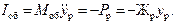

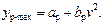


 и
и  - среднее значение и среднее квадратическое отклонение расчетной нагрузки;
- среднее значение и среднее квадратическое отклонение расчетной нагрузки;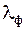 – нормирующий множитель, определяющий вероятность появления максимальной вертикальной нагрузки, значение
– нормирующий множитель, определяющий вероятность появления максимальной вертикальной нагрузки, значение 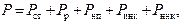
 – статическая нагрузка колеса на рельс;
– статическая нагрузка колеса на рельс;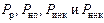 – динамические добавки от колебания кузова на рессорах, от неровности пути, изолированной неровности и непрерывной неровности на колесе.
– динамические добавки от колебания кузова на рессорах, от неровности пути, изолированной неровности и непрерывной неровности на колесе. принимаются равными нулю, исходя из того, что колебательный процесс в одном цикле совершается около нуля.
принимаются равными нулю, исходя из того, что колебательный процесс в одном цикле совершается около нуля.