
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Машины. Механизмы. Сборочные единицыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Машины. Механизмы. Сборочные единицы Маши́на (лат. machina — «механизм, устройство, конструкция», от др.-греч. μηχανή — «двигать») — техническое устройство, выполняющее механические движения для преобразования энергии Машины используются для выполнения определённых действий с целью уменьшения нагрузки на человека или полной замены человека при выполнении конкретной задачи. Механи́зм (греч. μηχανή mechané — машина) — внутреннее устройство машины, прибора, аппарата, приводящее их в действие. [1] Механизмы служат для передачи движения и преобразования энергии (редуктор, насос, электрический двигатель). Простая машина — механизм, который изменяет направление или величину силы без потребления энергии. Сборочная единица — изготовленое, изготавливаемое, или же подлежащее изготовлению изделие, состоящее из нескольких деталей, соединяемых в процессе его изготовления между собой в одну общую конструкцию, при помощи применения для этого различного вида сборочных операций (свинчивания, сочленения, клёпки, сварки, пайки, опресовки, развальцовки, склеивания, сшивания, укладки, и т.п.), например: автомобиль, станок, телефонный аппарат, микромодуль, редуктор, сварной корпус, маховичок из пластмассы с металлической арматурой. К сборочным единицам (при необходимости) также относят: а) изделия, для которых конструкцией предусмотрена разборка их на составные части предприятием-изготовителем, например, для удобства упаковки и транспортирования; б) совокупность сборочных единиц и (или) деталей, имеющих общее функциональное назначение и совместно устанавливаемых на предприятии-изготовителе в другой сборочной единице, например: электрооборудование станка, автомобиля, самолёта; комплект составных частей врезного замка (замок, запорная планка, ключи); в) совокупность сборочных единиц и (или) деталей, имеющих общее функциональное назначение, совместно уложенных на предприятии-изготовителе в укладочные средства (футляр, коробку и т.п.), которые предусмотрено использовать вместе с уложенными в них изделиями, например: готовальня, комплект концевых плоскопараллельных мер длины. Расчет на изгиб.
Расчет на изгиб Вал поддерживает сидящие на нем детали и передает крутящий момент вдоль своей оси. При работе испытывает, напряжения от изгиба и кручения (иногда от растяжения-сжатия). 1\\\\\ Разъемные соединения. Соедине́ние — процесс изготовления изделия из деталей, сборочных единиц (узлов), агрегатов путём физического объединения в одно цело · резьбовое соединение · штифтовое соединение · шпоночное соединение · шлицевое (зубчатое) соединение · байонетное соединение · клеммовое соединение · конусное соединение · профильное соединение · бугельное соединение · соединение шип-проушина
4 Основные требования к машинам и их деталям. К большинству проектируемых машин предъявляются следующие требования: – надежность; – высокая производительность; – ремонтопригодность; – экономичность производства и эксплуатации; – гарантированный срок службы и технологичность; – удобство и безопасность обслуживания; – небольшие габариты и масса; – транспортабельность; – соответствие внешнего вида требованиям технической эстетики. Критериями работоспособности деталей является их прочность, жесткость, износостойкость, виброустойчивость, теплостойкость. Прочность – важнейший критерий работоспособности детали, характеризует ее способность сопротивляться действию нагрузок без разрушения или пластических деформаций. Непрочные детали не могут работать. Жесткость характеризуется изменением размеров и формы детали под нагрузкой. Износостойкость. В результате изнашивания выходят из строя большинство подвижно соединенных деталей. Виброустойчивость. При высоких скоростях звеньев механизмов могут возникнуть вибрации, которые вызывают дополнительные переменные напряжения и, как правило, приводят к усталостному разрушению деталей. Теплостойкость. Тепловые расчеты при проектировании механизмов обычно производятся для решения двух задач: 1) определения температуры нагрева деталей и изыскания способов ограничения ее величины допустимыми пределами; 2) определения величины тепловых деформаций деталей для учета их влияния на точность и надежность механизма. Пренебрежение к учету влияния тепловых факторов может привести к чрезмерному и неравномерному нагреву деталей механизма и нарушению нормального их взаимодействия. Расчет осей валов. Определение модуля зубчатого колеса. Модуль зубчатого колеса геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности d д к числу зубьев z или отношению шага t по делительной окружности к числу: m = d д /z = ts /π. Для косозубых цилиндрических колёс различают: окружной модуль ms = d д /z = ts /π, нормальный модуль mn = tn /π, осевой модуль ma = tа /π, где ts, tn и ta — соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к. стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента
Внутренний крутящий момент При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения. Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T. Затем из условий равновесия остановленной части вала определяют крутящий момент:
T = Мк= Σ Мi
Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.
Угол сдвига
Напряжения при кручении Распределение касательных напряжений
Максимальное касательное напряжение
10)Виды движений Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние. Равномерное движение материальной точки — это движение, при котором величина скорости точки остаётся неизменной. Расстояние, пройденное точкой за время t, задаётся в этом случае формулой l = v t. Равномерное Прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковыеперемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.
Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты
где По определению инерциальной системы отсчёта, точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если векторная сумма всех сил, приложенных к точке, равна нулю. Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению. Примером такого движения является движение тела, брошенного под углом При равноускоренном движении по прямой скорость тела определяется формулой:
Зная, что
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. Поступательное движение — это механическое движение системы точек (абсолютно твёрдого тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.[1] В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе. Математически поступательное движение по своему конечному результату эквивалентнопараллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является кругом, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение. Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма. Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.
Зубчатая передача Передаточное отношение
Передаточное число зубчатой передачи – это отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса. Передаточное число зубчатой передачи определяется по формуле:
где Знак «+» берется для внешнего зацепления (рис.1 и рис.2), знак «–» для внутреннего зацепления. Виды зацеплений приведены на рис.2. Знаки учитываются только для зубчатых передач с параллельными осями вращения колес. Передаточное отношение ременной передачи рассчитывают так:
где n1 - число оборотов ведущего вала в с (мин); n2 - число оборотов ведомого вала в с (мин); D1 - диаметр ведущего шкива, мм (м); D2 - диаметр ведомого шкива, мм (м). Цепная передача
Передаточное отношение определяют из условия равенства средней скорости цепи на звездочках: Отсюда передаточное отношение, понимаемое как отношение частот вращения ведущей и ведомой звездочек, U=n1/n2=z2/z1, где n1 и n2—частоты вращения ведущей и ведомой звездочек, мин-1; z1 и z2 — числа зубьев ведущей и ведомой звездочек
12) Выбор электродвигателя привода
Общий коэффициент полезного действия (КПД) привода:
где
Расчетная требуемая мощность двигателя: Рт.р. = Рз / где Рз –мощность электродвигателя, Рз =2 кВт; Рт.р. = 2 / 0,885 = 2,33 кВт Определяем требуемое число оборотов двигателя:
где
По данным таблицы 5.1 приложения [1] принимаем электродвигатель 4А112МВ8У3, у которого:
S – скольжение, S = 3.7%; По формуле 5.7 приложения [1] определяем частоту вращения у нагруженного ротора:
13) Критерии прочности Критериями прочности в зависимости от класса материала, вида напряженного состояния (растяжение, сжатие, сдвиг и др.) и условий эксплуатации (температура, время действия нагрузки и пр.) могут быть временное сопротивление, предел текучести, предел усталости и другие виды сопротивления. Преде́л про́чности — механическое напряжение Предел текучести — механическое напряжение σт, отвечающее нижнему положению верхнего отклонения по площади неизвестной эпюры площадки текучести надиаграмме деформирования материала. В случае, если такая площадка отсутствует, что характерно, например, для хрупких тел, вместо σт используется условный предел текучести σ0,2 (читается: сигма ноль-два), который соответствует напряжению, при котором остаточная (пластическая деформация) составляют 0,2 % от длины испытываемого образца.[1] Часто для данной механической характеристики дают формулировку «напряжение, при котором начинает развиваться пластическая деформация»[2], не делая разницы с пределом упругости. В реальности значения предела текучести выше, чем предел упругости примерно на 5%.[3] σт=Fт/S0 Предел упругости — максимальная величина механического напряжения, при которой деформация данного материала остаётся упругой, то есть полностью исчезает после снятия нагрузки. Преде́л выно́сливости (также преде́л уста́лости) — в науках о прочности: одна из прочностных характеристик материала, характеризующих его выносливость, то есть способность воспринимать нагрузки, вызывающие циклические напряжения в материале. Предел выносливости материала определяют с помощью испытаний серий одинаковых образцов (не менее 10 шт.): на изгиб, кручение, растяжение-сжатие или в условиях комбинированного нагружения (последние два режима для имитации работы материала при асимметричных циклах нагружения или в условиях сложного нагружения). Цепная передача В подобной ременной передаче ремень может быть заменен на цепь, в этом случае шкивы также должны быть заменены на звездочки. Полученная передача называется цепной, она знакома каждому, ведь именно такая применяется на велосипедах. Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).Отличительной особенностью цепной передачи является повышенный уровень шума, а также износ при работе на высоких скоростях, поэтому ее при необходимости использования лучше всего ставить после уменьшения оборотов. В автомобиле возможно применение цепной передачи для привода ГРМ, правда, ограничением такого применения является повышенный уровень шума при ее работе Зубчатая передача. Так называется механизм, в котором используются колеса с зубьями, находящимися в зацеплении. Она считается наиболее рациональной и востребованной для машиностроения. Существует множество разнообразных вариантов изготовления подобных колес, отличающихся по расположению осей, форме зубьев, способу их зацепления и т.д. Как в случае с цепной, для зубчатой передаточное число определяется делением числа зубьев шестерен (z2/z1). Многообразие вариантов построения зубчатой передачи предоставляет возможность использовать их в разных условиях, от тихоходного редуктора до высокоточных приводов. Для зубчатой передачи характерны: · постоянное передаточное число; · компактность; · высокий кпд; · надежность. Одной из разновидностей зубчатой передачи считается червячная. Она используется в тех случаях, когда передача момента осуществляется между скрещивающимися валами, для чего применяется такой элемент как червяк, представляющий собой винт специальной конструкции с резьбой. Для определения передаточного отношения червячной передачи выполняют деление количества зубьев колеса (червячного) z2 на число заходов резьбы червяка z1. Планетарная передача Этот вид зубчатой передачи, содержащей колеса с геометрическими осями, имеющими возможность перемещения. Что она собой представляет, можно понять из приведенного ниже рисунка. По сути дела, это уже конструкция своеобразного планетарного редуктора, включающего в свой состав некоторое число шестерен, взаимодействующих между собой. У каждой из них свое название – солнце, корона, сателлит. Для такого планетарного редуктора изменение момента зависит от того, какая из его шестерен неподвижна, на какую подан крутящий момент, и с какой он снимается.
При любом использовании планетарного редуктора, один из трех его элементов будет неподвижен. У такого, планетарного варианта построения передач, по отношению к простой зубчатой или ременной, есть возможность получить существенное изменение момента при небольшом количестве колес и габаритах устройства. В автомобиле у подобного планетарного устройства своя сфера применения – в составе АКПП, а также в гибридных транспортных средствах, для обеспечения совместной работы ДВС и электромотора. Широкое применение планетарного редуктора осуществляется в гусеничной технике. Расчёты валов Проектировочный расчет валов выполняют на статическую прочность с целью ориентировочного определения диаметров отдельных ступеней. На стадии технического предложения известен только вращающий момент Т. Изгибающие моменты М можно определить только после разработки конструкции вала, когда становятся известны его длина и места приложения нагрузок. Поэтому проектировочный расчет вала выполняют условно только на кручение, но по пониженным допускаемым напряжениям [τ], исходя из формулы τ = T / Wp ≤ [τ], где Wp = πd3 /16 – полярный момент сопротивления, мм3; T, Н•м. Отсюда d' > 10[T / (0,2[τ])]1/3, мм, где [τ] = (0,025…0,03)σВ; σВ – временное сопротивление материала, МПа. Расчетный диаметр d ' округляют в большую сторону по ГОСТ 6636-69. Для валов редукторов d ' обычно соответствует диаметру конца входного (выходного) вала, местам под зубчатыми колесами на промежуточных валах. Диаметры других участков назначают при разработке конструкции вала с учетом их функционального назначения, технологии изготовления и сборки. По рассчитанному диаметру d разрабатывают эскизную конструкцию вала, устанавливают тип опор, ориентировочно выбирают подшипники и проводят проверочные расчеты вала на статическую прочность, на сопротивление усталости, на жесткость и на виброустойчивость. Проверочный расчёт
Зубчатые передачи. Зубчатой передачей называется механизм, служащий для передачи вращательного движения с одного вала на другой и изменения частоты вращения посредством зубчатых колес и реек. Зубчатое колесо, сидящее на передающем вращение валу, называется ведущим, а на получающем вращение — ведомым. Меньшее из двух колес сопряженной пары называют шестерней; большее — колесом; термин «зубчатое колесо» относится к обеим деталям передачи. Зубчатые передачи представляют собой наиболее распространенный вид передач в современном машиностроении. Они очень надежны в работе, обеспечивают постоянство передаточного числа, компактны, имеют высокий КПД, просты в эксплуатации, долговечны и могут передавать любую мощность (до 36 тыс. кВт). К недостаткам зубчатых передач следует отнести: необходимость высокой точности изготовления и монтажа, шум при работе со значительными скоростями, невозможность бесступенчатого изменения передаточного числа. В связи с разнообразием условий эксплуатации формы элементов зубчатых зацеплений и конструкции передач весьма разнообразны. Зубчатые передачи классифицируются по признакам, приведенным ниже. 1. По взаимному расположению осей колес: с параллельными осями с пересекающимися осями); со скрещивающимися осями. В зависимости от относительного вращения колес и расположения зубьев различают передачи с внешним и внутренним зацеплением. В первом случае вращение колес происходит в противоположных направлениях, во втором — в одном направлении. Реечная передача (рис. 172, IX) служит для преобразования вращательного движения в поступательное. 2. По форме профиля различают зубья эвольвентные и неэвольвентные, например цилиндрическая передача Новикова, зубья колес которой очерчены дугами окружности. 3. В зависимости от расположения теоретической линии зуба различают колеса с прямыми зубьями, косыми, шевронными и винтовыми В непрямозубых передачах возрастает плавность работы, уменьшается износ и шум. Благодаря этому непрямозубые передачи большей частью применяют в установках, требующих высоких окружных скоростей и передачи больших мощностей. 4. По конструктивному оформлению различают закрытые передачи, размещенные в специальном непроницаемом корпусе и обеспеченные постоянной смазкой из масляной ванны, и открытые, работающие без смазки или периодически смазываемые консистентными смазками. 5. По величине окружной скорости различают: тихоходные передачи (v равной до 3 м/с), среднескоростные (v равной от 3... 15 м/с) и быстроходные (v более 15 м/с). 18.Резьбовые соединения, их расчет. Резьбовое соединение — разъёмное соединение деталей машин при помощи винтовой или спиральной поверхности (резьбы). Это соединение наиболее распространено из-за его многочисленных достоинств. В простейшем случае для соединения необходимо закрутить две детали, имеющие резьбы с подходящими друг к другу параметрами. Для рассоединения (разъема) необходимо произвести действия в обратном порядке. В резьбовых соединениях используется метрическая и дюймовая резьба различных профилей в зависимости от технологических задач соединения. Достоинства и недостатки резьбовых соединений Недостатки резьбовых соединений: В качестве резьбовых элементов используют болты (винты с гайкой), винты и шпильки. Основным преимуществом болтового соединения является то, что оно не требует выполнения резьбы в соединяемых деталях и исключена необходимость замены и ремонта дорогостоящих корпусных деталей из-за повреждения резьбы. Винты применяются, когда корпусная деталь большой толщины не позволяет выполнить сквозное отверстие для установки болта. Шпильки используют вместо винтов, если прочность материала детали с резьбой недостаточна (сплавы на основе алюминия), а также при частых сборках-разборках соединений. Классификация и основные признаки резьб: Рис. 2.4
Проектный расчёт Основной габаритный размер передачи − делительный диаметр колеса по внешнему торцу − рассчитывают по формуле: где Е пр − приведённый модуль упругости, для стальных колёс T 2 − вращающий момент на валу колеса, Нмм (см.п.2.4);
Здесь Кbe − коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, Кbe = bw / Re. Рекомендуют принять
Рис. 2.5
Наиболее распространено в редукторостроении значение Кbe = 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид где u p– расчетное передаточное число конической передачи,
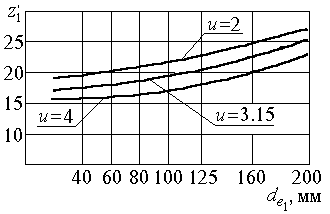
Геометрический расчёт Определяют делительный диаметр шестерни по внешнему торцу Число зубьев шестерни По значению Вычисленное значение z 1 округляют до целого числа.
Рис. 2.6
Определяют число зубьев колеса Вычисленное значение - передаточное число передачи - угол делительного конуса колеса - угол делительного конуса шестерни - внешний окружной модуль Рекомендуется округлить me до стандартного значения me ф по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров Рассчитывают величину внешнего конусного расстояния передачи (рис. 2.4) Рабочая ширина зубчатого венца колеса определяют как Полученное значение Определяют расчётный модуль зацепления в среднем сечении зуба При этом найденное значение mm не округляют! Рассчитывают внешнюю высоту головки зуба Внешнюю высоту ножки зуба определяют как Внешний диаметр вершин зубьев колёс рассчитывают по формуле Угол ножки зуба рассчитывают по формуле
Проверочный расчёт При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия где E пр − приведённый модуль упругости, для стальных колёс здесь
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.016 с.) |




 .
. точки от времени является линейной:
точки от времени является линейной: ,
, — начальная координата точки,
— начальная координата точки,  — проекция вектора скорости на координатную ось.
— проекция вектора скорости на координатную ось. к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением
к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением  , направленным вертикально вниз.
, направленным вертикально вниз.
 , найдём формулу для определения координаты x:
, найдём формулу для определения координаты x:
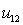 (иногда используется обозначение
(иногда используется обозначение  ) определяется при ведущем колесе 1, передаточное отношение
) определяется при ведущем колесе 1, передаточное отношение  определяется если ведущим является колесо 2:
определяется если ведущим является колесо 2: ,
, .
. и
и  ,
, и
и  - числа зубьев колес 1 и 2, соответственно.
- числа зубьев колес 1 и 2, соответственно.

 – КПД муфты,
– КПД муфты,  – КПД пары подшипников качения,
– КПД пары подшипников качения,  – КПД зубчатой передачи,
– КПД зубчатой передачи,  – КПД клиноременной передачи,
– КПД клиноременной передачи,  = 0,98·0,992·0,97·0,93 = 0,86
= 0,98·0,992·0,97·0,93 = 0,86 ,
, - число оборотов двигателя,
- число оборотов двигателя, 
 - передаточное число редуктора,
- передаточное число редуктора,  - передаточное ременной передачи,
- передаточное ременной передачи, 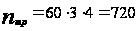 об/мин;
об/мин; - мощность двигателя,
- мощность двигателя, 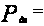 3 кВт,
3 кВт, - синхронная частота вращения,
- синхронная частота вращения,  750 об/мин,
750 об/мин, , выше которого происходит разрушение материала. Согласно ГОСТу 1497-84 более корректным термином является «Временное сопротивление разрушению», то есть напряжение, соответствующее наибольшему усилию, предшествующему разрыву образца при (статических) механических испытаниях. Термин происходит от того представления, что материал может бесконечно долго выдержать любую статическую нагрузку, если она создаёт напряжения меньшие по величине, чем временное сопротивление. При нагрузке, соответствующей временному сопротивлению (или даже превышающей её — в реальных и квазистатических испытаниях) разрушение материала (разделение образца на несколько частей) произойдёт через какой-то конечный промежуток времени, возможно, что и практически сразу.
, выше которого происходит разрушение материала. Согласно ГОСТу 1497-84 более корректным термином является «Временное сопротивление разрушению», то есть напряжение, соответствующее наибольшему усилию, предшествующему разрыву образца при (статических) механических испытаниях. Термин происходит от того представления, что материал может бесконечно долго выдержать любую статическую нагрузку, если она создаёт напряжения меньшие по величине, чем временное сопротивление. При нагрузке, соответствующей временному сопротивлению (или даже превышающей её — в реальных и квазистатических испытаниях) разрушение материала (разделение образца на несколько частей) произойдёт через какой-то конечный промежуток времени, возможно, что и практически сразу. ,
, МПа;
МПа; − коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис. 2.5.
− коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис. 2.5. . Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H 1 и H 2 > 350 HB или V > 15 м/с.
. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H 1 и H 2 > 350 HB или V > 15 м/с.
 ,
, или up = z 2 / z 1.
или up = z 2 / z 1. .
. назначают по рекомендациям, представленным на рис. 2.6.
назначают по рекомендациям, представленным на рис. 2.6. при Н 1 и
при Н 1 и  ,
,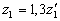 при
при 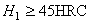 и
и  при Н 1 и
при Н 1 и  .
.
 .
. округляют до целого числа. После этого необходимо уточнить:
округляют до целого числа. После этого необходимо уточнить: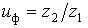 ,
, ,
, ,
, .
.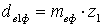 и
и  .
. .
. .
. округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5).
округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5). .
. .
. .
. .
. .
.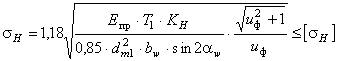 ,
, − вращающий момент на шестерне, Нмм,
− вращающий момент на шестерне, Нмм,  ;
; − КПД передачи.
− КПД передачи.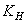 − коэффициент расчётной нагрузки,
− коэффициент расчётной нагрузки,  ; коэффициент концентрации нагрузки
; коэффициент концентрации нагрузки 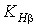 найден ранее по графикам рис. 2.5.
найден ранее по графикам рис. 2.5.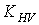 − коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости
− коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости  в соответствии с рекомендациями (табл. 2.6);
в соответствии с рекомендациями (табл. 2.6); − делительный диаметр шестерни в среднем сечении зуба,
− делительный диаметр шестерни в среднем сечении зуба,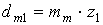 ;
; − угол зацепления, <
− угол зацепления, < 


