
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силовые зависимости в ременной передачиСодержание книги
Поиск на нашем сайте
Определение силы предварительного натяжения F0, Н, одного клинового ремня
число ремней - z Скорость ремня Окружная сила Ft, Н, передаваемая комплектом ремней
Сила давления на вал
Угол обхвата
Общий КПД привода определяется по формуле:
где Вращающие моменты
Выражение мощности
Выражение вращающего момента
Выражение вращающего момента
Связь между мощностями на ведущем и ведомом валах определяется следующей зависимостью:
9) Расчет на кручение Кручением называется такой вид нагружения (деформации), при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – крутящий момент T (рис 5.1). Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.
Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М1, М2, …, Мn или распределенными m по длине вала l. Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо сечении вала относительно его продольной оси.
Внутренний крутящий момент При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения. Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T. Затем из условий равновесия остановленной части вала определяют крутящий момент:
T = Мк= Σ Мi
Таким образом, крутящий момент в каком либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.
Угол сдвига
Напряжения при кручении Распределение касательных напряжений
Максимальное касательное напряжение
10)Виды движений Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние. Равномерное движение материальной точки — это движение, при котором величина скорости точки остаётся неизменной. Расстояние, пройденное точкой за время t, задаётся в этом случае формулой l = v t. Равномерное Прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковыеперемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.
Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты
где По определению инерциальной системы отсчёта, точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если векторная сумма всех сил, приложенных к точке, равна нулю. Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению. Примером такого движения является движение тела, брошенного под углом При равноускоренном движении по прямой скорость тела определяется формулой:
Зная, что
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. Поступательное движение — это механическое движение системы точек (абсолютно твёрдого тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.[1] В общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе. Математически поступательное движение по своему конечному результату эквивалентнопараллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является кругом, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение. Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма. Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 906; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.171 (0.01 с.) |

 . (3.9)
. (3.9) – коэффициент угла обхвата, назначаемый по рекомендации
– коэффициент угла обхвата, назначаемый по рекомендации – коэффициент длины ремня, назначается по табл. 3.4 в зависимости от отношения расчетной длины ремня L к базовой L0;
– коэффициент длины ремня, назначается по табл. 3.4 в зависимости от отношения расчетной длины ремня L к базовой L0;  – коэффициент передаточного отношения, назначаемый по табл. 3.5;
– коэффициент передаточного отношения, назначаемый по табл. 3.5;  – коэффициент режима нагрузки, назначаемый по табл. 2.9.
– коэффициент режима нагрузки, назначаемый по табл. 2.9.
 . (3.10)
. (3.10) – допускаемая скорость
– допускаемая скорость . (3.11)
. (3.11) ремнем ведущего шкива
ремнем ведущего шкива ,
, – число элементов привода, в которых происходит потеря мощности (передачи, опоры, муфты).
– число элементов привода, в которых происходит потеря мощности (передачи, опоры, муфты). и
и 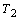 , соответственно, между ведущим и ведомым валами связаны следующей зависимостью:
, соответственно, между ведущим и ведомым валами связаны следующей зависимостью: .
. , Вт, через окружное (тяговое) усилие
, Вт, через окружное (тяговое) усилие  , Н, и окружную скорость
, Н, и окружную скорость  , м/с, зубчатого колеса, шкива, барабана, звездочки и т.д. имеет следующий вид:
, м/с, зубчатого колеса, шкива, барабана, звездочки и т.д. имеет следующий вид: .
. , Н·м, через мощность
, Н·м, через мощность  , рад/с, имеет следующий вид:
, рад/с, имеет следующий вид: ;
;  .
. , м, имеет следующий вид:
, м, имеет следующий вид: .
.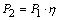 .
.


 .
. точки от времени является линейной:
точки от времени является линейной: ,
, — начальная координата точки,
— начальная координата точки,  — проекция вектора скорости на координатную ось.
— проекция вектора скорости на координатную ось. к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением
к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением  , направленным вертикально вниз.
, направленным вертикально вниз.
 , найдём формулу для определения координаты x:
, найдём формулу для определения координаты x:



