
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Иллюстрация качественного и количественного анализаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Качественный анализ дерева происшествий. В ходе качественного анализа левой части модели рис. 4.2 удалось выявить 27 минимальных пропускных сочетаний: два из которых включают по одному исходному событию (синглеты) – 12 и 13, двадцать состоят из двух предпосылок (дуплеты) - 3,7;...;4,11; пять имеют по три исходных события (триплеты) - 5,6,7;...;5,6,11. Боле того в рассматриваемом нами дереве имеются также три минимальных отсечных сочетания: 1,2,3,4,5,12,13; 1,2,3,4,6,12,13 и 7,8,9,10,11,12,13. Анализ этих данных на качественном уровне свидетельствуют, что из учитываемых нами событий нижнего уровня наиболее значимы для появления исследуемых происшествий – 12 и 13, наиболее критичны для их предупреждения - 5 и 6, тогда как все остальные исходные предпосылки в этом смысле качественно равнозначны. Более точные выводы дает количественный анализ, проведенный с помощью такой структурной функции дерева происшествия: Х=ИÚЛ=(ВÙЕ)ÚЛ=[(АÚ1Ú4ÚБ)Ù(ГÚД)]ÚЛ= =[3Ú(1Ú2)Ú4Ú(5Ù6)]Ù[(7Ù8)Ú(9ÚД)]ÚЛ= =[3Ú(1Úv2)Ú4Ú(5Ù6)]Ù[(7Ú8)Ú9Ú(10Ú11)]Ú(12Ú13). (4.1) Напомним, что символы "Ú", "Ù" здесь означают булевы операторы дизъюнкции и конъюнкции, соответствующие условиям "или", "и". Количественная оценка вероятности происшествий. Прогноз вероятности возникновения головных событий исследуемого дерева происшествия - Q(X) может быть осуществлен двумя путями: а) заменой в выражении (4.1) кодов событий оценками вероятности их появления, а операторов "Ú" и "Ù" - арифметическими действиями "+" и "´", с последующим проведением необходимых преобразований и вычислений; б) с помощью выявленных выше минимальных сочетаний исходных предпосылок - по формулам (2.9) и (2.10), при условии, что входящие в них параметры принимают следующие значения: а=27: m=2 для i=1...20; т =3 для i=21...25 и m=1 для i=26,27; b=3, nk=7 - для всех значений k. Так, после подстановки вероятностей Pi в формулу (2.9), имеем: Q(X) = 1-[(1-P3P7)(1-P3P8)(1-P3P10)(1-P3P11)(1-P2P7)´ ´(1-Р2Р8)(1-Р2Р9)(1-Р2Р10)(1-Р2Р11)(1-Р1Р7)(1-Р1Р8)´ ´(1-Р1Р9)(1-Р1Р10)(1-Р1Р11)(1-Р4Р7)(1-Р4Р8)(1-Р4Р9)´ ´(1-P4P10)(1-P4P11)(1-P5P6P7)(1-P5P6P8)(1-P5P6P9)´ ´(I-P5Р6Р10)(1-Р5Р6Р11)(1-Р12)(1-Р13)= 0,0013...0,0967. (4.2) Аналогичный результат получается и с помощью формулы (2.10):
Q(X) = [1-(1-Р3)(1-Р2)(1-Р1)(1-Р4)(1-Р5)(1-Р12)(1-Р13)]´- ´[1-(1-Р3)(1-Р2)(1-Р1)(1-Р4)(1-Р6)(1-Р12)(1-Р13)][1-(1-Р7)´ ´(1-P8)(1-P9)(1-P10)(1-P11)(1-P12)(1-P13)]=0,0013...0,0967, (4.3) где Q(X) и Рi (i =1...13) - соответственно вероятности рассматриваемых происшествий и предпосылок к ним - событий из табл. 4.1- 4.2. Поясним, что нижняя граница значений вероятности появления исследуемых нами происшествий, найденной по формулам (4.1- 4.4), относится к аварии, а верхняя - к несчастному случаю. Приближенная оценка этих вероятностей (пренебрежение слагаемыми и сомножителями - имеющими более высокий порядок малости) может быть осуществлена с помощью структурной функции (4.1); Q(X)=(P1+P2+P3+P4)(P7+P8+P9+P10+P11)+P12+P13=0,001...0,083. (4.4) Как видим, погрешность подобных формул (при Р£0,01 и числе входящих в них исходных предпосылок - п£ 10-12) не превышает 15% от значения, рассчитанного по точным формулам. Полученные выше результаты оценки Q(X) нужно истолковывать следующим образом: при заданных исходных данных, частота возможных железнодорожных несчастных случаев примерно в восемьдесят раз выше аварий на летательных аппаратах, приходящихся в среднем один раз на тысячу их заправок. Однако сравнение тяжести исследуемых происшествий по этим результатам провести невозможно: нужен соответствующий анализ дерева событий. Прогноз среднего ущерба от происшествия. Для иллюстрации работоспособности процедур расчета экономических последствий рассматриваемых происшествий, воспользуемся данными, приведенными в скобках правой части рис. 4.2 для некоторых исходов истечения и трансформации выброса АОХВ. Напомним, что имеющиеся там первые цифры указывают на вероятности, а вторые - на количество пролитого горючего - К и размеры площади - П возможных зон поражающего действия взрыва, пожара и токсичных паров, соответственно. Из этих данных, в частности, следует, что верхнее ответвление дерева характеризует последствия большого пролива топлива: 375 т водорода образовали ТВС, взрыв которой привел к разрушениям на площади около 6 га. Средний предполагаемый объем пролитого горючего может быть оценен с учетом других ветвей дерева - как математическое ожидание соответствующей случайной величины: M(K)= 0,4×375+0,3×60+0,3×16=172,8 т. Ожидаемая при этом средняя площадь поражения фугасными, термическими и токсичными факторами оказалась равной: М(П) =0,3×6+0,1×2+0,1-1=2,1 га.
Прогноз ущерба от фугасных факторов. Оценим, для примера, степень фугасного разрушения трехэтажного кирпичного завода, имеющего высоту 12 м и предназначенного для производства криогенного горючего (жидкого водорода). Здание имеет степень фронтального (к взрыву) остекления 30% и расположено на удалении от места заправки летательного аппарата в 100 м. При этом в качестве модели причинения ущерба используем формулы (3.6-3.12). Определение давлений ВУВ, воздействующих на здание завода, проведем в следующей последовательности. Вначале по формуле (3.12) найдем тротиловый эквивалент облака испарившейся смеси: q =0,044×0,5×2,73×375×2/4,52»10000 кг. Коэффициенты здания рассчитаем по формуле (3.7): КН =1+(3,4/12)=1,28 и КР =[(1,36+0,3)2+0,3(1-0,3)]0,5-0,36=1,35. Затем, используя данные табл. 3.5 и эти коэффициенты, по формуле (3.8) оценим усредненное, а затем и все пороговые давления: DРjср=1,28×1,35×13=22,46 кПа, Dj1 =22,46(0,07+0,37×1)=9,88 кПа, DРj2 =18,19 кПа; DРj3 =26,50 кПа и DРj4 =34,81 кПа. Руководствуясь выражением (3.6), найдем величину давления на фронте ВУВ в месте расположения завода. С учетом приведенного расстояния X ф =100/(10 000)1/3=4,64 м/кг1/3, ее значение равно: DРФ ={[(1,60 + 0,91×4,64)/4,64]2-1}×103,32=59,37 кПа. Оценку среднеожидаемой степени повреждения завода осуществим с помощью формулы (3.8): iср =0,71[(59,37/46)-0,30]=2,52, а вероятности причинения ущерба конкретной степени тяжести - по графикам рис. 3.3 (при iср =2,52). Оказывается, что они равны: для первой степени поражения Qj1 =0,08; для второй - Qj2=0,40, для третьей – Qj3 =0,42 и для четвертой – Qj4 =0,10. Наконец, величина ущерба, причиненного заводскому зданию, может быть рассчитана по формулам (3.10 и 3.11). Его относительная стоимость Сiср =1-ехр(-0,05×2,522,4)=0,37=37%. В единицах социального времени: а) число работающих - Niср =2(9+0,015-0,37×4000)=62 чел; б) продолжительность работ ticp =(7,2×0,37×4000)/62=172 дн; в) трудоемкость - 62×172=10664 чел×дн. При стоимости одного человеко-дня, равной в настоящее время примерно 50 руб, такой ущерб оценивается в 533200 руб. Прогноз концентрации вредных веществ. Проиллюстрируем теперь изложенные выше способы прогнозирования концентрации вредных веществ на примере оценки возможности воспламенения паров пролитого, но не взорвавшегося горючего - жидкого водорода. Сделаем это на момент достижения соответствующим облаком завода по его производству, расположенного на таких удалениях от места аварии: х1=100, x2 = 20 и x3=10 м. Предположим также, что масса пролитого и мгновенно испарившегося горючего K=М= 16000 кг, а метеорологические условия в момент аварии характеризуются отрицательным вертикальным температурным градиентом в 0,5 град/м и скоростью ветра в направлении оси x1, равной u1 =3 м/с. Для прогноза концентрации паров водорода, используем приведенное в предпоследней строке табл. П3.3 общее решение модели 101301, считая, что t =40 с. Естественно, что при указанной выше скорости ветра, с учетом его отклонения от оси x1 на 20 м, облако достигнет завода за это время. Входящие в модель коэффициенты турбулентной диффузии определим с помощью табл. П3.5 и П3.2 - для класса устойчивости атмосферы D. Оказывается, что в этом случае (для условий сельской местности) K1 =К2 =12,1×3 = 36,3 м2/с и K3 =1,07×0,3 =3,21 м2/с. После подстановки соответствующих исходных данных в выбранную нами математическую модель и проведения вычислений, имеем:
c(x, t) = (16000)/[8(3,14×40)3/2(36,3×36,3×3,21)1/2]×exp[-(100-3×40)2/(4×36,3×40) – 202(4×36,3×40)]×[exp(-102/(4×3,21×40)]+exp[-102/(4×3,21×40)]]=16000/(52776×520)× ×4,43×1,65=0,00424 кг/м3. Сравнение данной концентрацией с нижним и верхним концентрационными пределами распространения пламени в рассматриваемой топливовоздушной смеси (0,00412...0,072кг/м3) свидетельствует о возможности воспламенения соответствующего облака, в случае попадания в него открытого огня. Оценку теплового поражения не защищенных термостойкой одеждой людей, спешно покидающих аварийную стартовую площадку и уже отбежавших от здания завода на 325 м, проведем в соответствии с рекомендациями главы 3. В соответствии с формулами (3.14) имеем такие параметры огненного шара: Dош =55×161/3=138 м, Еош =12,3×161/3=78,1 ГВт, tош = Dt =3,8×161/3=9,5c. Удельный импульс q оценим делением мощности огненного шара на площадь сферической поверхности с радиусом, равным расстоянию между его центром и местоположением людей: q =78,1-109/4 p (70+325)2=39,85 КВт/м2. Вероятность их гибели от поглощенной тепловой дозы найдем с помощью табл. 3.4 и табл. 3.3: Pi= -36,4+2,56/n(9,5×39,954/3)=6,41 и Q=0,93. Прогноз эффективности мероприятий по снижению риска. В завершение приведем два примера, иллюстрирующих возможность обоснования рекомендаций по совершенствованию безопасности с помощью имеющихся у нас моделей. Будем считать, что для повышения безопасности путевых рабочих, могут быть использованы, например, такие четыре средства: 1) звуковые сигнализаторы индивидуального оповещения людей о приближающемся поезде; 2) сигнально-блокировочная система предотвращения въезда поезда на участок работ; 3) локомотивное устройство "Спасатель"; 4) временное ограждение места работ. Рассматриваемые технические средства способны повлиять в первую очередь на те предпосылки, которые имеют номера 13, 8, 9 и 11 (напомним, что первая из них имеет наивысшую значимость). При этом предполагается, что их внедрение уменьшит соответствующие вероятности до следующих величин: P13= 0,0015, Р8= 0,004, Р9 =0,0015 и Р11 =0,0005. Пусть также указанные четыре средства защиты работающих требуют для их внедрения таких затрат: С13 = С9 =500 руб, а C8=C11=2000 руб. Поочередная подстановка новых значений перечисленных вероятностей в приближенную формулу (4.4), дает такие значения соответствующего параметра головного события: Q13(x) = 0,0029, Q8(X) = 0,00347, Q9(X) = 0,00348 и Q11(X) = 0,003. Сравнение же этих средств по критерию "затраты-эффект" между собой и с прежней вероятностью травмирования Q(X) =0,08385, указывает на предпочтительность внедрения звуковых сигнализаторов индивидуального оповещения и временного ограждения места работ. По крайней мере, они эффективнее двух других альтернативных технических средств обеспечения безопасности работ по пневмоочистке железнодорожного пути.
Аналогичным образом могут быть выбраны оптимальные мероприятия, необходимые для повышения безопасности исследуемой заправки. Прежде всего за счет организационно-технических мероприятий, понижающих вероятности возникновения наиболее значимых и критичных исходных предпосылок. Ожидаемые от внедрения подобных мероприятий изменения DРI (i=5,6,12,13) следует оценивать методами теории надежности в технике или теории эрготехнических систем, а обусловленный ими эффект: DРI ® DQi(X)® ®DMi[Y] -только что рассмотренными и проиллюстрированными в работе методами моделирования опасных процессов в техносфере. Рассмотренные выше иллюстративные примеры подтверждают перспективность предложенных моделей и методов исследования опасных процессов в техносфере. Более того, они показали их практическую пригодность для априорной оценки и оптимизации мероприятий по снижению техногенного риска. А без этого нельзя решить столь сложную проблему, каковой является ныне обеспечение и совершенствование производственно-экологической безопасности современного производства и транспорта. Решение задачи оптимизации затрат на обеспечение безопасности и ущерба от возможных происшествий проиллюстрируем на примере технологического процесса погрузочно-разгрузочных операций, выполняемого бригадой из двух человек с помощью автокрана типа КС-3572. При этом используем реальные показатели этого оборудования и статистические данные о частоте и тяжести происшествий при проведении аналогичных перегрузочных работ. Предполагаем, что размеры среднего ущерба при работах оценивались параметром Y = 660 усл. единиц (см. табл. П.4.6). Длительность задержек при их выполнении по этой же причине - Z = 6 рабочих дней.
где zi – задержки времени при возникновении конкретных предпосылок развития происшествия; n – общее количество предпосылок. Примечание: не все предпосылки могут вызвать задержки времени. Предельно допустимые потери времени от аварийности и травматизма - Td(Pd) = 5 дней при продолжительности исследуемого периода Т= 7 лет. Предельно допустимые потери времени от аварийности и травматизма определяются из выражения (3.51) Tд(Pd) £ Qд(t)×Z или Tд(Pd) = к× Qд(t)×Z, где к – коэффициент, определяющий сложность человекомашинной системы (к= 0,2…1,0); Qд(t) – вероятность возникновения головного события (происшествия) за исследуемый период. Определение затрат на обеспечение безопасности данного процесса проводилось с учетом стоимости используемых при работах технических и технологических средствах защиты (приборов безопасности): ограничителя грузоподъемности. тормозных устройств, средств блокировки, индикатора опасных напряжений, указателей угла крена и маневра: затрат на создание запаса прочности силовых элементов автокрана, трудозатрат на техническое освидетельствование и обслуживание его ответственных узлов; расходов на отбор, обучение и воспитание работающих по технике безопасности.
Трудозатраты на предупреждение аварийности и травматизма учитываем в человекоднях, стоимость одного из которых была принята равной 50 руб. В итоге оказалось, что расходы на обеспечение безопасности работ в течение семи лет составили величину, равную примерно 80 таким усл. единицам. Трудозатраты на предупреждение аварийности и травматизма можно ориентировочно оценить с помощью следующего эмпирического выражения S=k× Tд(Pd)× 50, где k - коэффициент, определяющий сложность человекомашинной системы (k= 0,3…0,8); На основе имеющихся статистических данных о количестве происшествий при аналогичных перегрузочных работах был оценен параметр потока происшествий vпр = 4,8×10-4 1/час работы. Примечание: при отсутствии статистических данных об vпр значение параметра потока происшествий (интенсивности отказов за одну технологическую операцию) может быть определено путем пересчета вероятности возникновения происшествия в течение технологической операции, полученной при анализе дерева происшествий, в интенсивность отказов за один час. При интенсивности работ, равной 360 перегрузкам в год и длительности одной из них t =20 мин, общая продолжительность функционирования рассматриваемых человекомашинных систем за 7 лет составила t = tk×wkпр×Т= 0,33×360×7=840 час. Это позволяет рассчитать вероятность не возникновения происшествий за этот период выполнения работ. Pd(t)= ехр-(vпр×T) = ехр-(0,00048-840) =0,668 и значение параметра затрат С = 80×((1-0,668)/0,668 = 40 усл. единиц. Найденным оценкам С и Y соответствует следующее значение вероятности Pd*(t)= Проверка полученных результатов на удовлетворяемость ограничениям задачи (3.45) осуществлена путем контроля справедливости условий (3.48) и (3.51). Подстановка значений соответствующих оценок в смысловое и структурное ограничения соответственно дала: C/Y= 80(1 – 0,6682) / 162×0,668 = =0,41<1 и 1- 0,754 < 5/7, или иначе: 0,246 < 0,714. Эти неравенства позволили сделать вывод о возможности использования значения Рd (t = 7 лет) = 0,754 в качестве оптимального, точнее - экономически приемлемого (при принятых предположениях) уровня безопасности рассматриваемых перегрузочных работ.
Построение графика Значение Mt[Y] выбираем согласно таблице П. 4.6. (Последствия происшествий на оборудовании). Ожидаемые средние затраты на обеспечение безопасности проводимых работ — Мt [S] изменяем в пределах ±30% с шагом 10% минимум. Каждое из полученных значений подставляем в формулу (3.47) и получаем значения параметра затрат С с учетом вероятности невозникновения происшествия. Математическое ожидание величины ущерба от аварийности и травматизма Mt[Y] варьируем в тех же пределах ±30% и шагом. Затем поочередно подставляем Mt[Y] и Мt [S] в формулу (3.46), причем сначала оставляя неизменным среднее значение Мt [S], меняя лишь Mt[Y], а затем наоборот, при постоянном среднем Mt[Y] меняем Мt [S]. Далее воспользуемся формулами (3.43) и (3.42), где Pd(t) заменяем на Pd*(t), рассчитанные нами ранее. Рассмотренные постановка и решение задачи нормирования уровня безопасности — обоснования оптимального по суммарным издержкам значения вероятности выполнения работ без происшествий проиллюстрированы на рис. 3.4.
Рис. 3.4 Графическая интерпретация задачи
Данная прямая будет смещаться вправо — по мере снижения затрат Мt[S] или увеличения ущерба Mt[Y], что равносильно уменьшению С и увеличению Y соответственно.
ЗАКЛЮЧЕНИЕ
Данная работа помогает устранить дефицит в учебно-методической литературе по системному обучению, оценке обеспечению, совершенствованию производственно-экологической безопасности и будет полезна соответствующим специалистам. Тем более, что в ней изложен наиболее перспективный подход к решению данной проблемы, основанный на моделировании опасных процессов в техносфере. Конечно, изложенные рекомендации не во всех случаях представляются как завершенные и дающие достаточно точные прогнозы техногенного риска. Не все из них проиллюстрированы конкретными примерами - в силу трудоемкости соответствующих расчетов и необеспеченности ресурсами. Большинство этих и других возможных издержек работы вызваны сложностью рассматриваемых человекомашинных систем и недостаточной достоверностью имеющихся данных об их количественных параметрах. Несмотря на трудоемкость системного подхода к моделированию опасных процессов в техносфере, именно он позволяет поставить решение рассматриваемой проблемы на действительно научную основу. Без системного подхода трудно надеяться также на успех в декларировании безопасности и страховании опасных производственных и транспортных объектов. Именно системный подход к моделированию опасных процессов в техносфере является необходимым условием решения столь актуальной ныне проблемы, связанной с производственно-экологической безопасностью.
ПРИЛОЖЕНИЯ
П1. СПРАВОЧНЫЕ ДАННЫЕ О БЕЗОШИБОЧНОСТИ ЧЕЛОВЕКА
Таблица П1.1. Экспериментальные характеристики безошибочности среднестатистического человека
Продолжение Табл. П1.1.
Таблица П.2.1.
Диапазоны изменения безошибочности человека (интенсивности ошибок)
Примечание: выбор значений интенсивностей ошибок из указанных диапазонов производится в зависимости от сложности пультов, количества элементов индикации, сложности алгоритма операторских действий, уровня стрессовых воздействий и т.п.
П.2. СПРАВОЧНЫЕ ДАННЫЕ О БЕЗОТКАЗНОСТИ ТЕХНИКИ Таблица П2.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.25 (0.017 с.) |


 ,
,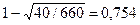 , а обусловленный возможными происшествиями допустимый ущерб за это же время составил: М[Y] =(1- 0,754)× 660=162 усл. ед.
, а обусловленный возможными происшествиями допустимый ущерб за это же время составил: М[Y] =(1- 0,754)× 660=162 усл. ед.



