
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы прогноза концентрации вредных веществ в зонахСодержание книги
Поиск на нашем сайте
Актуальность и состояние вопроса. Анализ приведенных выше способов прогноза ущерба людским и природным ресурсам свидетельствует о том, что вероятность и тяжесть его причинения химическими или радиоактивными веществами нельзя оценить, не зная полей их концентрации - c(x,t). Сложность заблаговременного и достоверного определения таких функций предопределена тремя основными группами факторов: а) источник - его геометрия, расход, термодинамические параметры; в) среда - температурная и скоростная стратификация на макроуровне, ее микронеоднородность, нерегулярность, турбулентность; в) вредное вещество - плотность, размер частиц, их склонность к физико-химическим превращениям после контакта со средой и ограничивающей поверхностью. Известные ныне подходы (модели и методы) определения функций c(x,t) также можно разделить на три важные группы: а) аналоговые (автомодельные); б) аналитические (гауссовы); в) численного моделирования. Исходными данными и средствами их верификации служат результаты статистических наблюдений, натурных и модельных экспериментов, получаемые и обрабатываемые методами теории подобия или другими специальными способами. Естественно, что каждый подход к определению функций c(x,t) имеет свои достоинства и недостатки. Численное моделирование не заменимо для прогноза последствий истечения мощных струй и мгновенных выбросов большого количества веществ, имеющих существенно отличную от несущей среды температуру или плотность, т.е. - при разрушениях газопроводов, взрывах токсичных продуктов и проливах сжиженных природных газов [11]. Основанный на процессах массо-, энерго- и теплообмена данный метод позволяет учесть практически все перечисленные выше наиболее существенные факторы, а потому является самым точным, но (одновременно) и самым трудоемким способом построения полей концентраций вредных веществ. В большинстве случаев, однако, используются аналоговые (автомодельные) и аналитические (гауссовы) модели и методы прогнозирования полей концентрации загрязнителя в зонах его рассеяния. Первые из них хорошо зарекомендовали в случаях, когда наблюдается устойчивая корреляция между моделью и оригиналом по большинству их основных факторов (источник, вредное вещество, несущая среда) [1,2]. Последние модели и методы, основанные на закономерностях турбулентной диффузии и вероятностно-статистических представлениях о рассеянии загрязнителей, не требуют трудоемких расчетов и экспериментов, а потому лучше всего подходят для экспресс-прогноза зон их концентрации [8]. Гауссовы (диффузионные и дисперсионные) модели корректно использовать при небольших возмущающих термодинамических воздействиях потока вещества-загрязнителя на несущую среду. В противном случае можно получить необоснованно завышенные значения c(x,t). Последнее имеет место, например, при раздвоении облака паров сжиженного тяжелого газа и обусловлено игнорированием гауссовыми моделями специфики распределения поля скоростей в зоне его испарения - мощных нисходящих потоков в центре пролива и таких же, но в обратном направлении по его периметру. Кодирование моделей. При использовании аналитических (гауссовых) моделей, их удобно классифицировать по следующим признакам: а) теоретический базис: 1 - модели диффузионного обмена, 2 - модели дисперсионного обмена; б) размерность источника загрязнения: 0 - точечный, 1 - линейный, 2 - площадной; в) временной режим работы источника выбросов: 1 - практически мгновенно, 2 - неустановившийся (в течение времени т с переменной интенсивностью), 3 -установившийся (t®¥) и 4 - эпизодические залповые выбросы вредного вещества; г) размерность загрязняемой зоны: 1 - одномерная, 2 - двумерная, 3 -трехмерная; д) активность вещества: 0 - инертный, 1 - неинертный, подверженный химическим или фазовым превращениям; е) условия на границах зоны рассеяния: 0 - нулевая концентрация при больших удалениях, 1 - полное отражение и 2 - поглощение вредного вещества на границе. Ниже будем оперировать функциями c(x,t), приведенными в табл. П3.3 и П3.4 приложения к данной работе для моделей, обозначенных шестизначным позиционным кодом, цифры {0...4} в каждой позиции { а...е } которого указывают на перечисленные выше признаки. При этом предпочтение будет отдано моделям турбулентной диффузии, как более точным. А вот дисперсионные модели, включая и ту, которая положена в основу нормативной методики [15], следует применять в случае крайней необходимости - для сравнения c(x,t) или получения официального заключения. Базовые модели. Интересующие нас функции c(x,t), описывающие динамику концентрации вредного вещества в точках зоны загрязнения с координатами х =(x1,x2,x3), могут быть получены как явно выраженные аналитические решения такой полуэмпирической диффузионной модели турбулентности:
где с - средняя концентрация вредного вещества в момент времени t в точке х =(x1,x2,x3); и, - средняя скорость движения несущей среды вдоль i -ой координатной оси в точке x; Ki - коэффициент турбулентной диффузии (турбулентного обмена) вдоль i -ой оси; R(c) - скорость убыли вещества-загрязнителя за счет химических и фазовых превращений; S(x,t) - функция источника загрязнений, определяющая скорость изменения их концентрации в среде за счет ее подпитки вредным веществом. Решение данного дифференциального уравнения в частных производных для мгновенного выброса М (кг) вредного вещества из точки x в неограниченную трехмерную среду в момент времени t=t-t0 при допущениях: Кi=const, ui=const, R(c)=0, t0=0, а также с учетом "нулевых" начальных и граничных условий, имеет такой вид[8]:
Частные случаи. Из фундаментального решения (3.18) могут быть получены более конкретные зависимости, приведенные в табл. П3.З и П3.4 приложения. Каждая из них характеризуется своей интенсивностью выброса вредного вещества в единицу времени из точки, с погонного или квадратного метра (соответственно для точечного, линейного и площадного источников), а также определенными значениями скоростей несущей среды - ui, моментов времени - t, координат источника – хi’ и коэффициентов: Ki - турбулентного или si - дисперсионного обмена между нею и веществом-загрязнителем. Таблица П3.3 содержит диффузионные модели полей концентрации вредного вещества. Три ее первые строки относятся соответственно к точечному, линейному и площадному источникам - как для неустановившегося (выброс продолжается), так и для стационарного режимов. В четвертой строке этой таблицы приведены результаты для установившегося режима (t®¥): точное (общее) решение - для удалений Две последние строки табл. П3.3 содержат сведения о полях концентрации вредного вещества в зоне вокруг источника, расположенного на поверхности земли или воды, являющейся границей этих двух сред и воздуха. Отметим, что в этом случае (при x3’=0) экспоненты в фигурных скобках становятся одинаковыми. При отражении вредного вещества одной средой, это приводит к увеличению функции c(x,t) в 2 раза по сравнению с аналогичным выражением, когда отражение не учитывается. В случае же поглощения вещества-загрязнителя, разность экспонент в фигурных скобках, да и сама функция (концентрация на границе) становятся равными нулю, т.е. со временем соблюдается условие: c(x,t) =0. Табл. П3.4 содержит дисперсионные модели динамики изменения концентрации загрязнителя по координатам пространства зоны его рассеяния. Как уже упоминалось, данные решения не являются строгими, поскольку получены при довольно грубом допущении - о зависимости дисперсий только от расстояния и неизменности во времени. Заметим, что более корректные модели дисперсионного обмена могут быть получены из диффузионных моделей табл. П3.3 -после введения в них подстановки Кi=si2/2. Однако при получении формул табл. П3.4 такая цель не преследовалась, поэтому к ним следует относится как к - приближенным, дающим завышенные оценки функции c(x,t). Первые три строки табл. П3.4 относятся к мгновенным выбросам вредного вещества из точечного, линейного и площадного источников соответственно: четвертая и пятая - к стационарному распределению загрязнений от точечного и линейного источников. Две последние модели получены при двух дополнительных допущениях: а) совпадение направления ветра с осью X1, б) несущая среда считается однородной и стационарной. Особенности определения параметров c(x,t). Как показывает анализ таблиц П3.3 и П3.4, помимо координат и времени, другими базовыми параметрами содержащихся в них функций c(x,t) служат коэффициенты турбулентного – Кi и дисперсионного - si обмена. Сразу отметим, что их определение является одной из самых серьезных трудностей, с которой сталкиваются при прогнозировании полей концентрации вредных веществ в зонах их рассеяния. Укажем также, что статистическая интерпретация этих коэффициентов такова: Ki=(1/2)dsi2(t)/(dt); si2(t)=å[xi(t)-xi(to)]2, а сложности их априорной оценки обусловлены следующими факторами. Во-первых, Кi и si, зависят как от свойств среды, которая сама по себе чрезвычайно изменчива, так и от степени ее возмущения вредными выбросами и их источником; во-вторых, эти коэффициенты являются функцией не только расстояния от источника выбросов, но и от времени их начала to. Более того, характер зависимости этих параметров от времени t=t-to не постоянен: с помощью корреляционной функции поля скоростей можно показать, что при малом времени рассеяния, si2~t2 и Ki~t, а при большом, - si~t; и К i ®const [1]. Определение коэффициентов Кi. С учетом вышеизложенного, приведем рекомендации, необходимые для определения входящих в модели коэффициентов турбулентной диффузии. Сделаем это для трех важных случаев: 1) атмосфера в зоне рассеяния вредных веществ считается невозмущенной; 2) среда в зоне выброса загрязнителя возмущена мощной струей источника; 3) среда возмущена выбросом большого объема тяжелых газов. В первом случав для определения коэффициента турбулентной диффузии атмосферы -KA, следует пользоваться такой формулой [1]:
где k - постоянная Кармана, равная для этих условий 0,4±0,4; u* - динамическая скорость (мера интенсивности диффузии), м/с; х3 - высота относительно подстилающей поверхности, м; ra - плотность атмосферы (несущей среды), кг/м3 tпп - напряжение трения в подстилающей поверхности (Па), зависящее от ее шероховатости; g - ускорение земного притяжения, м/с2, L - характерный масштаб длины Монина-Обухова, определяемый для приземного слоя по такой зависимости: L = u*3/[ k(g/To)-(q/(Cpr)], (3.20) где Ср, То - удельная теплоемкость воздуха при постоянном давлении, кДж/(кг×град) и его средняя температура в приземном слое, °С; q - турбулентный поток тепла, кДж/ м2×с; Заметим, что в приведенных выше формулах g /То и q/Cpr учитывают влияние воздействия таких сил: первая дробь - архимедовых, вторая - турбулентного переноса тепла, а и* играет роль масштаба скорости; при этом два последних компонента (3.20) не изменяются по высоте приземного слоя, равной примерно 10 м. Помимо оценки К„ изложенный выше подход может быть использован для определения средней скорости вертикального распространения примесей -и(Хз): и(Хз) = (и*)[f(x3/L)-f(x30/L)]/k. (3.21) где xзо - высота шероховатости (см), вводимая для удовлетворения граничных условий (равенства нулю этой скорости при xз =0); f(xэ/L) -функция безразмерной высоты, рассчитываемая для малых (xэ/L) по такой формуле: f(xэ/L)=lп ï xз/L ï +0,6 xэ/l Во втором случае (атмосфера возмущена мощной струей) величина коэффициента турбулентного обмена – Кs определяется исходя из доказанного А. Колмогоровым, Л. Прандтлем и Е. Хирстом факта о пропорциональности его значения кинетической энергии турбулентности - скорости смешения, примерно равной скорости турбулентных пульсаций - \/е [1,11]: KS=zC×b×(r /ra)0,75×Ve; (3.22) Ve={0,08 ï [0,5gwb(r /ra)-1/UR3] ï } ×[ ï (UR2-uUa)/UR ï+4,5ï wUa/UR) ï ] где zC, b - эмпирический коэффициент, зависящий от формы струи (для круга он равен 0,3) и радиус струйного истечения, м; ïï, A, S - знак модуля, индексы при параметрах атмосферы и струи; w,UR - скорость истечения вредного вещества из источника в направлении оси xз и модуль скорости результирующего потока, м/с. В третьем случа е (для рассеяния газов с плотностью r >rа +0,01) коэффициенты турбулентного обмена определяются с помощью соотношений Г. Копенбрандера, Т. Спайсера и Д. Хавенса, которые учитывают связи между ними и параметрами, описывающими состояние несущей среды и характер ее термогазодинамического возмущения [1]: К1=К2=cК3; K3=(k× u* × x3)/[0,88+0,099•Ri*1,04)(1+g)]; Ri*=(r-ra)gheff/rau*2; /heff= (I/C0) где К1, К2, К3 - коэффициенты турбулентной диффузии в направлениях, совпадающих с осями x1, x2, x3; c - безразмерный множитель, определяемый для различных степеней вертикальной устойчивости атмосферы по табл. 3.10. Ri* - массовое число Ричардсона (безразмерный параметр, характеризующий термическую устойчивость атмосферы, здесь R Ri* >0); heff - эффективная высота вредного облака, м; Со, С - концентрации вредных веществ: максимальная на оси облака и соответствующая конкретной его высоте, кг/м3 Таблица 3.10
Примечание: Критерии оценки классов устойчивости (стабильности) атмосферы приведены в табл. П3.6 приложения. Входящий в табл. 3.10 класс устойчивости (стабильности) атмосферы следует определять по табл. П3.2 или П3.6 приложения. При этом подразумевается такая связь между принятыми в них наименованиями: классы А, В и С означают конвекцию (соответственно - сильную, умеренную и слабую), класс D - изотермию. а классы Е, F - инверсию (умеренную и сильную). Сложнее рассчитать эффективную высоту - heff, введенную для согласования теории с экспериментом, поскольку точное значение этого параметра может быть определено лишь численным моделированием. Как показывают результаты [11], например, для рассеяния тяжелых газов при классе устойчивости атмосферы F, данная высота изменяется в пределах [2...8] м. Следовательно, в приближенных расчетах можно использовать значения heff из этого интервала, при условии, что меньшие значения эффективной высоты должны соответствовать вредным примесям тяжелее воздуха, а большие - равным или легче ему по плотности. Оценка дисперсий si. Для определения входящих в табл. П3.4 дисперсий si, воспользуемся рекомендациями [15], где их величина считается зависящей от параметров несущей среды, шероховатости подстилающей поверхности и удаления от источника выброса:
s1=C3×x1/(1+0,0001x)1/2; s3=j(x30,x1) ×q(x1);
q(x1)=A1xB1/(1+A2xB2); (3.24) s3ôконвекция<640 м; s3ôизотермия<400 м; s3ôинверсия<220 м, где U - скорость ветра, совпадающего с осью x1, м/с; А1,А2,В1,В2,С3 - коэффициенты, характеризующие вертикальную устойчивость атмосферы (определяются с помощью табл. 3.11); C1,C2,D1,D2 - коэффициенты, зависящие от шероховатости местности в зоне распространения вредных веществ (см. табл. 3.12). Учитывая громоздкость определения дисперсий s1 и коэффициентов Кi укажем более простой способ их приближенный оценки, предложенный авторами [2,8,9]. При известных параметрах вертикальной устойчивости атмосферы и шероховатости конкретной местности, они предлагают рассчитывать показатели турбулентного и диффузионного обмена как функцию одного параметра: а) s1 - от расстояния между конкретной точкой пространства и источником выбросов – х (м), б) Ki - от скорости ветра в приземном слое - V (м/с): K1=K2=Y1,2×V; K3=Y3×V; s1=ai×x×(1+b1×x)ci, (3.25) где Y1,Y2, Y3 и ai,bi,ci - константы, значения которых приведены соответственно в табл. П3.5 и П3.7 приложения. Таблица 3.11
Таблица 3.12
Сопоставление результатов оценки коэффициентов турбулентной диффузии К„ полученных с помощью у, и % (см. табл. П3.5 и 3.10), указывает на их удовлетворительное согласие, особенно для условий сельской местности. Это свидетельствует о возможности применения данного способа оценки К, для моделирования турбулентного рассеяния вредного вещества из приземных источников, в открытой местности. Достигнутая при этом погрешность не превышает ту, которая обеспечивается известными ныне дисперсионными моделями. Здесь не приводятся другие модели рассеяния вредных веществ основанные на уравнениях термогазодинамики и имеющие более сложные начальные и граничные условия [1]. Примеры, иллюстрирующие возможности рассмотренных моделей при прогнозировании вредных концентраций в зонах поражения различных ресурсов, будут приведены в заключительной главе настоящих методических рекомендаций.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.34 (0.011 с.) |

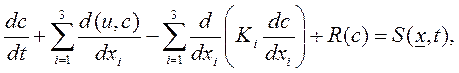 (3.17)
(3.17) (3.18)
(3.18) и приближенное - для сильно вытянутого (вдоль направления перемещения среды) облака вредных загрязнений, иногда называемого "факелом".
и приближенное - для сильно вытянутого (вдоль направления перемещения среды) облака вредных загрязнений, иногда называемого "факелом".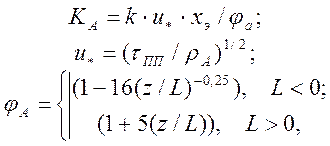 (3.19)
(3.19) (3.23)
(3.23)




