
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ущерб от стойкой утраты трудоспособности человекаСодержание книги
Поиск на нашем сайте
Нетрудно показать, что стоимость одного человеко-дня может быть выражена и в эквивалентном ему денежном исчислении. Для определения его величины, следует поделить суточный валовой национальный доход государства или конкретной отрасли на число работающих, т.е. найти прибавочную стоимость одного работника за вычетом расходов на его жизнеобеспечение. В отдельных случаях можно исходить из субъективной оценки стоимости жизни или размеров страховых выплат на случай гибели человека. Ущерб биоресурсам. По мнению авторов [5], ущерб от гибели флоры и фауны следует оценивать по ослаблению энергонасыщенности соответствующих экосистем, потоки входящей - I и выходящей - E энергии, которая проходит через трофические уровни пирамид питания. Величину ущерба можно считать пропорциональной энергопродуктивности уничтоженных биоресурсов. При этом стоимость энергии, утилизируемой ими автотрофно, должна сопоставляться с затратами на ее получение другими, "экологически чистыми" способами. (Например, - солнечными электробатареями, при цене 5 долларов США за 1 Вт/ч). Для определения энергонасыщенности биоты, необходимо располагать следующими исходными данными: средняя масса тела одной биоособи – MK (кг), энергетическое содержание накопленного ею вещества – gK (кДж/кг), скорость оборота или регенерации данной биомассы - VK (1/год), энергия ее существования (интенсивность дыхания поддержания) - EK (кДж/год), трофические (пищевые) уровень и специализация - j, а также коэффициенты утилизации энергии на всех k –ых трофических уровнях –Рj. Стоимости подвергнутых разрушительному техногенному воздействию биотических природных ресурсов k - го вида – СK или покрытой ими единицы территории (акватории) - Ct могут быть рассчитаны по следующим формулам [5]:
где GK - энергосодержание погибших биоособей, кДж, Ci, Di - эквивалентная цена одной особи или единицы биомассы (кДж) и их плотность в зоне поражения биоты (1/га) или (1/км2). Заметим, что входящие в формулы (3.32) параметры стоимости рассчитываются с учетом временного лага, необходимого для полного восстановления поврежденной биоты, a Pj -безразмерная величина.
Методика расчета биоущерба. При определении параметров формул (3.32), целесообразно руководствоваться такими рекомендациями и справочными данными. 1. Величина энергетического содержания конкретных биоособей – GK, значение данного параметра определяется перемножением удельной теплоёмкости их тела - qK (кДж/кг) на его массу MK: GK = qK × MK (3.33) Данные по удельным теплоемкостям биомассы некоторых представителей флоры и фауны приведены в таблице П.4.3. 2. Скорость оборота или регенерации биомассы - VK. Ее величина считается пропорциональной среднему времени генерации особей конкретного вида, которое можно считать равным примерно одной трети максимальной продолжительности их жизни - tk. Иначе говоря: VK = tk× LK, где tk измеряется секундами. В отсутствие данных по tk максимальная длительность жизни млекопитающих и птиц рассчитывается по следующим формулам: tkм = 366×106 ×M 0,2; tkп = 894 × 106 ×W 0,19 . (3.34) 3. Энергия существования или мощность поддержания животных – ЕКЖ ирастений - ЕКР. Для большинства теплокровных животных она зависит от массы и примерно вдвое превышает уровень их основного обмена в термонейтральных условиях YКЖ. Следовательно, значения ЕКЖ и YКЖ для них определяются формулами: ЕКЖ = 2 × YКЖ; YКЖ = c×Md, (3.35) где c, d – коэффициенты аллометрического уравнения (см. табл. П.4.4) Определение ЕКР для растений в общем случае проводится с учетом процессов фотосинтеза и дыхания – исходя из затрат энергии на поглощение ими двуокиси углерода и выделение кислорода. Для лесных сообществ она может быть оценена в предположении, что их годичная продукция составляет 5% от общей биомассы, которая рассосредоточена так: в стволах – 40%, в ветвях и листьях – 35%, под землей – 25%. В пересчете на один кубометр древесины, величину ЕКР следует рассчитывать по такой формуле: ЕКР = 0,026688 ×r, (3.36) где r - плотность условно сухой древесины (см. табл. П.4.5). Коэффициент утилизации энергии – Pj. Для большинства плото- и зерноядных животных его значение можно принимать приблизительно равным 0,8. При питании животных грубыми зелеными кормами, величина Pj = 0,6.
Оценка ущерба от загрязнения атмо- и гидросферы. В заключение укажем на особенности оценки ущерба, обусловленного непрерывными выбросами загрязняющих веществ в природную среду. В соответствии с требованиями [16], для производственных и транспортных предприятий в расчетном периоде устанавливаются различные нормативы выплат за данные вредные выбросы: а) в пределах установленных для них лимитов –K1; б) сверх них –К2 (руб/усл.т). Эти выплаты предназначаются для снижения либо компенсации соответствующего социально-экономического ущерба. В случае не превышения предельно допустимых выбросов, величина выплат S1 (руб) за них в атмосферу и водные объекты определяется следующим образом:
где t, T - год планового периода и его общая продолжительность; St, StL - затраты на снижение токсодозы вредных выбросов в текущем году и приведенный лимит таких выбросов, установленный с учетом вида загрязняющих веществ, их допустимого объема и предельно допустимых концентраций в атмосферном воздухе или воде, соответственно. При превышении объема предельно допустимых выбросов, соответствующие издержки предприятий –S2 (руб.) рассчитываются таким образом: S2=Sjt /dMjt, (3.38) где Sjt -затраты предприятия, необходимые для достижения установленного лимита выбросов, руб./год; dMjt - плановый приведенный объем вредных выбросов, установленный предприятию в текущем году. Более подробные рекомендации, справочные данные и иллюстративные примеры определения размеров ущерба от непрерывных вредных выбросов приведены в [16]. Задача оптимизации соотношения затрат на обеспечение безопасности производственных и технологических процессов и возможного ущерба при возникновении происшествий может быть сформулирована следующим образом. Найти такое значение вероятности Pd(t) безопасного (без происшествий) их проведения (или эксплуатации конкретных образцов либо комплексов соответствующего оборудования) в течение заданного времени, при котором обеспечивается минимум суммы средних затрат - Mt[S] и ожидаемого среднего ущерба - Мt[Y], при условии, что средние ожидаемые задержки - Mt[Z] за это же время, не превысят их допустимого значения – Tд(Pd). Более строгая (по сравнению с данной - содержательной) постановка задача может быть выражена следующей системой математических выражений:
Первое слагаемое целевой функции R(Pd) = Мt[S] + Mt[Y] представляет собой затраты, необходимые при создании и эксплуатации производственного (технологического) оборудования для обеспечения его надежности и эргономичности, оснащения техническими и технологическими средствами защиты. В последующем, в эти затраты будут включены расходы на отбор, обучение и воспитание работающих по технике безопасности, создание комфортных условий рабочей среды, внедрение других организационно-технических мероприятий по предупреждению аварийности и травматизма. Анализ известных экономических исследований по безопасности показывает, что размеры затрат Мt[S(Pd)] находятся в существенной зависимости от вероятности Pd(t), однако точное аналитическое определение функции S[Pd(t)] в настоящее время затруднено. Данная зависимость может быть представлена следующим достаточно универсальным выражением:
S[Pd (t)] = S0 + [dS(Pd)/d Pd]D Pd, (3.40) где S0 - доля исходных затрат системы обеспечения безопасности; dS(P)/dPd и DPd - величина приращения этих затрат, зависящая от прироста вероятности Pd, и размеры этого прироста, соответственно. Для определения правой части приведенной аналитической зависимости, исследован характер изменения затрат на обеспечение безопасности при варьировании вероятности Pd(t). Оказалось, что повышение требуемой вероятности невозникновения происшествий связано обычно с ростом затрат S[Pd(t)], причем его интенсивность dS(P)/dPd резко возрастает по мере приближения вероятности Pd(t) к единице. Это обусловлено тем, что обеспечение совершенно безопасных ситуаций на современном энергоемком производстве, предусматривающих абсолютную безотказность и эргономичность оборудования, совершенно безопасные технологические режимы его использования по назначению, полное исключение ошибок работающих и опасных воздействий рабочей среды, требует (при данных технологиях "безопасности") неоправданно высоких, практически бесконечных затрат S[Pd(t)]. В то же время, при уменьшении требуемой величины вероятности непоявления происшествий - Pd(t), значение этих затрат также уменьшается; при этом можно допустить, что величина S[Pd(t)] будет стремиться к некоторой константе – S0, по мере приближения значения Pd(t) к другому граничному (нулевому) значению. Приведенные результаты указывают на возможность дальнейшей, более точной аппроксимации неявно заданной правой части уравнения (3.40) некоторым выражением, удовлетворяющим условиям:
Не исключая других адекватных аналитических функций, обеспечивающих систему (3.41), рассмотрим для примера аппроксимацию затрат на предупреждение аварийности и травматизма при проведении конкретного процесса следующим простейшим выражением: S[Pd (t)] = Mt[S] = C Pd (t)/[1- Pd (t)], (3.42) где С - некоторый параметр затрат, принятый неизменным на определенном уровне развития технологии обеспечения безопасности рассматриваемого процесса. В последующем будет показано, что значение введенного в выражение (3.22) параметра С - пропорционально расходам, необходимым для повышения уровня безопасности использования соответствующего оборудования на один процент. Величина данного псевдопостоянного параметра выражается в единицах измерения затрат на обеспечение безопасности (человекоднях или эквивалентных им по стоимости денежных единицах). Второе слагаемое целевой функции задачи оптимизации (3.39) – Mt[Y] является ожидаемым средним ущербом от аварийности и травматизма в течение времени t. Содержание данной категории рассмотрено в предыдущем параграфе, а величина соответствующего параметра определяется размерами людских, природных и материальных ресурсов, выведенных из строя или поврежденных в результате происшествий (прямым ущербом), а также затратами на проведение расследований, внеплановых инструктажей и других, обусловленных данными инцидентами мероприятий (косвенными издержками). К сожалению, представленное формулой (3.18) выражение не может быть использовано для расчета ущерба заблаговременно, т.к. содержит ряд заранее неизвестных параметров, таких как k, Cmk и Y.
Учитывая сложность априорного представления зависимости Y[Pd(t)], для приближенного определения рассматриваемого ущерба на конкретном производстве, может быть использована величина среднего ущерба Y от одного происшествия, найденная с помощью статистических данных. Ее значение, выражаемое также в трудозатратах или денежном исчислении, будет определяться типом производственного или технологического процесса и особенностями его проведения: энергоемкостью применяемого оборудования, составом взаимодействующих с ним сил и средств, последствиями возможных происшествий. Размеры среднего ущерба Y от однотипных происшествий в отдельных отраслях также могут быть приняты в первом приближении независимыми от вероятности возникновения. Такое допущение будет справедливо для всех тех процессов жизнедеятельности людей, которые имеют достаточно высокую безопасность проведения на сравнительно небольших интервалах времени. Анализ статистических данных о происшествиях подтверждает отсутствие каких-либо корреляций между величиной среднего ущерба от появления, например, какого-либо несчастного случая или аварии и их частотой либо вероятностью возникновения. Данный факт может быть, по-видимому, объяснен чисто психологически - только при реальной возможности (значительной вероятности) появления происшествий, человек начинает готовиться к ним заблаговременно и принимать меры к снижению возможного ущерба. На основании принятых допущений, значение второго слагаемого целевой функции системы уравнений (3.99) может быть определено по следующей формуле: Mt[Y]= Y[ 1 - Pd(t)]. (3.43) где Y - средние размеры ущерба от одного происшествия конкретного типа (катастрофы, аварии, несчастного случая) при проведении рассматриваемого процесса. Заметим, что данное выражение является частным случаем классического расчета математического ожидания случайной величины, т.к. получается заменой случайных переменных Pj и Yj, на их усредненные оценки. Входящая в ограничение рассматриваемой задачи величина ожидаемых средних задержек процесса вследствие аварийности и травматизма - Mt[Z(Pd)] может быть определена аналогичным образом - как приближенная оценка математического ожидания соответствующей случайной величины. Такое допущение обусловлено одной и той же природой экономического ущерба и его разновидности - задержек работ по причине происшествий. Если принятое допущение справедливо, то можно записать, что имеет место такое равенство:
Mt[Z] = Z[1- Pd (t)]. (3.44)
где Z - средние потери времени проведения конкретного процесса вследствие возникновения одного происшествия. С учетом принятых уточнений, математическая постановка задачи по обоснованию требований к уровню безопасности принимает вид: Система (3.45) представляет собой запись постановки задачи оптимизации со структурным и смысловым ограничениями (см. рис. 3.5), которая может быть решена классическим методом поиска экстремума, при условии последующей проверки полученного решения на их удовлетворяемость. В ней предполагается, что правая часть первого (структурного) ограничения к оптимизируемому параметру – Tд(Pd)/Z не может быть больше единицы, поскольку трудно вообразить, чтобы заведомо допускалось появление одного и более происшествий, т.е. соблюдалось неравенство: Tд(Pd) > Z. YPd2(t) – 2YPd (t) + Y – C = 0 Взятие первой производной по Pd(t) от целевой функции и приравнивание полученного выражения нулю, приводит после несложных преобразований к квадратному алгебраическому уравнению:
решение которого дает следующее, удовлетворяющее условиям задачи (3.19), значение искомой вероятности: Соотношение между ожидаемыми средними затратами Mt[S] и предполагаемым средним ущербом Mt[Y], при котором справедливо условие C/Y£ I, может быть получено из формул (3.42) и (3.43). После подстановки значений C = Mt[S]×[1 - Pd (t)]/Pd (t) и Y = Mt[Y/[1 - Pd (t)] (3.47) в условие C/Y £ 1, получается неравенство, определяющее область допустимых значений параметров С и Y: C/Y = [1 - Pd (t)]2 / Pd (t)Mt[Y] < 1 (3.48) Подчеркнем, что данное условие, при реальных значениях Pd(t), трансформируется в - более очевидное: (0,01 - 0,3) Mt[S] £ Mt[Y]. При решении задачи (3.39) в принципе могут встречаться различные соотношения между величиной вероятности, рассчитанной по формуле (3.46), и наименьшим из ее значений, найденным по ограничению к размеру – Тд(Рd). В реальных ситуациях с результатами ее решения необходимо руководствоваться следующими правилами. Если полученное значение Pd*(t) удовлетворяет структурному ограничению нашей задачи (находится внутри области допустимых значений), то найденное решение является требуемым. В случае не выполнения этого условия, ее оптимальное значение определяется исходя из предъявленных ограничений к допустимым задержкам Z, Тд(Рd). Укажем способ приближенного оценивания параметров С, Тд(Рd), Y и Z, необходимых для обоснования требований к уровням безопасности разрабатываемых процессов, который основан на использовании статистических данных о показателях работ, аналогичных по структуре и технологии выполнения. Для определения оценок Pd(t) и Mt[S] могут быть применены сведения о частоте происшествий, их последствиях, материальных и трудовых затратах на предупреждение аварийности и травматизма. В предположении о сравнительно малой изменчивости параметра С на отдельных этапах развития конкретных отраслей хозяйства, его оценка может быть рассчитана по зависимости (3.27): С =Mt[S][1- Pd(t)]/ Pd(t), (3.49) где Mt[S], Pd(t) - оценки средних затрат на предупреждение происшествий и вероятности безопасного проведения аналогичных процессов соответственно. Размеры среднего ущерба от аварийности и травматизма - Y, а также величина средних задержек времени работ по этой же причине - Z определяются для конкретных производственных и технологических процессов так же, как и ранее (см. 2.2.3) - по следующим зависимостям:
где l - количество типов происшествия (авария, несчастный случай, катастрофа), возможных при проведении исследуемых процессов; Yj, Zj - средний материальный ущерб и средние потери времени в результате появления одного происшествия J- го типа соответственно. Входящая в ограничение системы (3.45) величина Tд(Pd) определяется следующим образом. При известных значениях задержек Z в процессе выполнения аналогичных работ, ее можно рассматривать как долю этой величины Tд(Pd) £ Z. Отсюда следует, что для достигнутых на аналогах значений Qд(t), ограничение к величине допустимых задержек времени проведения разрабатываемого процесса может определяться из такого соотношения: Qд(t) = 1 - Pd (t)£ Tд(Pd)/Z. (3.51) Анализ полученных ранее данных показывает, что требуемые значения Pd(t) должны увеличиваться по мере роста среднего ущерба от одного происшествия или снижения параметра С, пропорционального расходам и трудозатратам, необходимым для повышения уровня безопасности проведения технологических процессов на один процент. Данный факт свидетельствует о необходимости дифференцированного подхода к установлению требуемых значений показателей безопасности разрабатываемых производственных и технологических процессов или эксплуатации используемого при этом оборудования. Нормировать безопасность необходимо строго индивидуально: с учетом достигнутого в отрасли уровня безопасности, расходов, необходимых для его повышения на один процент и серьезности последствий от возможных происшествий.
Глава 4. МЕТОДИКА МОДЕЛИРОВАНИЯ Принятая энергоэнтропийная концепция (см. главу 1), а также приведенные выше рекомендации по прогнозированию происшествий при проведении опасных процессов (глава 2) и ущерба от них (глава 3) позволяют сформулировать типовую методику априорной количественной оценки техногенного ущерба и проиллюстрировать ее работоспособность на конкретных примерах. Одна из возможных процедур прогноза техногенного риска, связанного с деятельностью отдельных производственных и транспортных объектов, подробно рассматривается ниже.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.016 с.) |

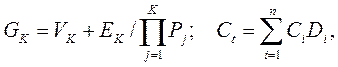 (3.32)
(3.32)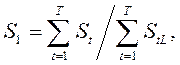 (3.37)
(3.37)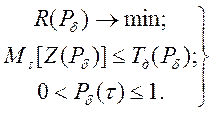 (3.39)
(3.39)
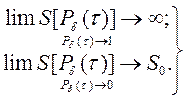

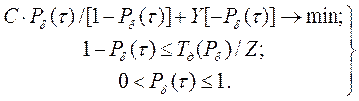
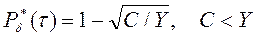 (3.46)
(3.46)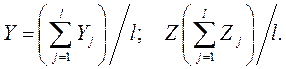 (3.50)
(3.50)


