
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование неявных функцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть Продифференцировав по х обе части уравнения Производные высших порядков находятся по той же схеме. Пример. Найти производную второго порядка функции заданной неявно
Решение. Найдем производную первого порядка
Выразим
теперь вынесем
и выразим
Найдем Для этого продифференцируем обе части полученного уравнения, считая y функцией от х
Производная функции, заданной параметрически
Пусть функция y от х задана параметрическими уравнениями
тогда Производная второго порядка находится по формуле Пример. Найти производную второго порядка функции заданной параметрически
Решение. Найдем
тогда Найдем тогда
Задания 3.
1) Найти производную указанного порядка. 2) Найти производную n -го порядка. 3) Найти производную второго порядка функции заданной неявно 4) Найти производную второго порядка функции заданной параметрически
Применение производной Приложение производной к задачам геометрии и механики
Если кривая задана уравнением Уравнение касательной к кривой Нормалью к кривой называется прямая, перпендикулярная к касательной и проходящая через точку касания. Уравнение нормами имеет вид: Угол между двумя кривыми Угол находится по формуле Если при прямолинейном движении точки задан закон движения
Пример: Какой угол образует с осью абсцисс касательная к кривой Решение. Найдем производную
т.е. Пример: Составить уравнение касательной и нормами к кривой
Решение. Найдем производную из уравнения кривой
определим значение производной в точке
Уравнение касательной будет:
Уравнение нормами
Пример: Найти угол между параболами Решение: Найдем координаты точки
Получилось две точки, назовем их Продифференцируем уравнение парабол Найдем угловые коэффициенты касательных к параболам в точке Следовательно также определяем угол между кривыми в точке Пример: Зависимость пути от времени при прямолинейном движении точки задана управлением
( Решение: Скорость определим из условия
ускорения Теперь определим
Задание 4.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 757; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.163.234 (0.01 с.) |

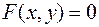 определяют y как неявную функцию от х. Будем считать, что функция дифференцируема.
определяют y как неявную функцию от х. Будем считать, что функция дифференцируема. .
.







 или
или 
 .
.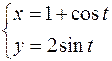

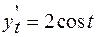

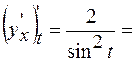

 ,
, 
 ,
, 





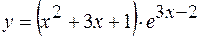 ,
, 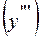
 ,
, 





 ,
,  ,
, 
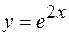




 ,
,  ,
, 






 ,
,  ,
, 
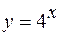
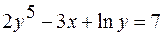

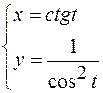

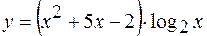 ,
,  ,
, 





 ,
,  ,
, 


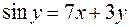
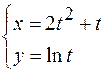

 ,
,  ,
, 



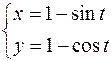

 ,
,  ,
, 




 ,
,  ,
, 





 ,
,  ,
, 

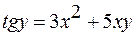



 ,
,  ,
, 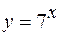




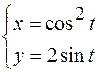
 ,
,  ,
, 





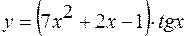 ,
,  ,
, 

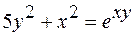



 ,
, 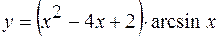 ,
, 




 , то
, то  , где
, где  -угол, образованный с положительным направлением оси
-угол, образованный с положительным направлением оси  касательной к кривой в точке с абсциссой
касательной к кривой в точке с абсциссой  :
: в точке
в точке  имеет вид:
имеет вид:  где
где  -есть значение производной
-есть значение производной  при
при 

 и
и  в точке их пересечения
в точке их пересечения 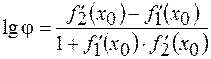
 , то скорость движения в момент времени
, то скорость движения в момент времени  есть производная пути по времени
есть производная пути по времени  , а ускорение, есть производная скорости по времени, или производная второго порядка пути по времени
, а ускорение, есть производная скорости по времени, или производная второго порядка пути по времени или
или 
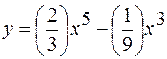 , проведенная в точке с абсциссой
, проведенная в точке с абсциссой  .
.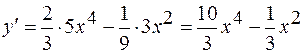 при
при  , получим
, получим 
 , а угол
, а угол 
 в точке
в точке 

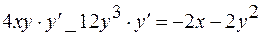
 тогда
тогда 

 или
или 
 или
или 
 ;
; 
 , точки пересечения парабол, для этого решаем уравнение:
, точки пересечения парабол, для этого решаем уравнение: ;
;  ;
;  ;
; 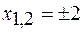 ;
; и
и 
 ;
; 

 ;
; 

 ;
; 

 в секундах;
в секундах;  в метах) определить скорость движения и ускорение в конце второй секунды
в метах) определить скорость движения и ускорение в конце второй секунды
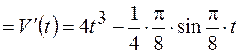
 и
и  в конце второй секунды, т.е. подставим, в найденные уравнения
в конце второй секунды, т.е. подставим, в найденные уравнения  секунды получим:
секунды получим:




