
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бумага писчая. Печать оперативная. Усл. п.л. 3,25.Стр 1 из 4Следующая ⇒
Бумага писчая. Печать оперативная. Усл. п.л. 3,25. Тираж 500 экз. Заказ № 10.
© Самарский государственный университет путей сообщения, 2008
Содержание
Введение
Настоящее пособие является практическим приложением к разделу «Дифференциальное исчисление». Пособие содержит практические задания, соответствующие разделам «Дифференциальное исчисление» и «Применение производной». Каждый раздел содержит вопросы для проработки теоретического материала, типовые задания с детально разработанным решением, задания для самостоятельного решения в объеме 30 вариантов.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Производная функции
Определение производной
Рассмотрим функцию Разность Если существует предел (конечный или бесконечный)
то он называется производной (конечной или бесконечной) функции Для производной функции
Замечание. Приращение Геометрический смысл производной заключается в том, что производная функции
Механический смысл производной – это скорость Пример. Найти по определению производную функции Решение. Зафиксируем произвольную точку Отсюда,
Так как в качестве
Например, Пример. Найти по определению производную функцию Решение. Зафиксируем произвольную точку
Следовательно,
Воспользовавшись непрерывностью функции
получаем
Так как в качестве
Например,
Производные основных элементарных функций
Приведём производные основных элементарных функций.
Пример. Найти производные следующих выражений: а) Решение. Каждая из данных функций является степенной функцией, поэтому все производные находятся по формуле а) б) с)
Производные суммы, разности, произведения и частного
Производные суммы, разности, произведения и частного двух функций
Пример. Найти производную функции Решение.
Пример. Решение. Сначала найдем производную функции
Итак,
Пример. Найти производную функции Решение.
Пример. Найти производную функцию Решение.
Производная сложной функции Пусть функция
Для краткости используется следующая запись последней формулы:
Пример. Найти производную функции Решение. Обозначим
откуда Пример. Найти производную функции Решение.
Пример. Найти производную функции Решение.
Задание 1.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.85 (0.036 с.) |
 , определённую на некотором интервале
, определённую на некотором интервале 
 называется приращением аргумента
называется приращением аргумента  в точке
в точке 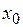 . Разность
. Разность 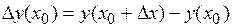 называется приращением функции
называется приращением функции 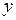 в точке
в точке 

 и обозначается
и обозначается  .
. используются следующие обозначения:
используются следующие обозначения:
 функции
функции  . Однако, не следует забывать, что эта величина зависит от точки
. Однако, не следует забывать, что эта величина зависит от точки  .
. , где
, где  – угол между касательной и положительным направлением оси абсцисс.
– угол между касательной и положительным направлением оси абсцисс. изменения пути
изменения пути  по времени
по времени  .
. .
. . Так как
. Так как  , то
, то  и
и  ,поэтому
,поэтому  .
. ,
, Следовательно,
Следовательно,


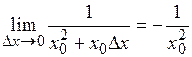
 можно взять любое число неравное нулю, то для любого числа
можно взять любое число неравное нулю, то для любого числа  получаем
получаем .
.
 .
. , то
, то 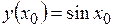 и
и  , поэтому
, поэтому .
. ,
, и первым замечательным пределом
и первым замечательным пределом ,
,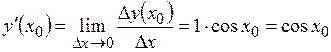 .
.
 .
.
 ;
; ;
;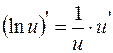 ;
; ;
; ;
; ;
; ;
; ;
;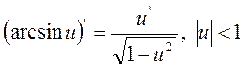 ;
;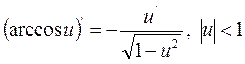 ;
; ;
;
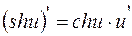 , где
, где  ;
; , где
, где  ;
; , где
, где  ;
; , где
, где  ; б)
; б)  ; в)
; в) 
 . Имеем:
. Имеем: ;
; ;
; .
. или
или  находятся по следующим формулам:
находятся по следующим формулам: ;
;  ;
;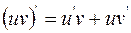 ,
,  , с – число,
, с – число, .
. .
.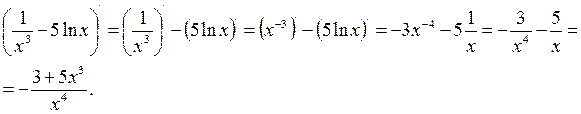
 , найти
, найти 
 :
:
 . Теперь находим значения производных при конкретных значениях
. Теперь находим значения производных при конкретных значениях  :
:

 .
.
 .
.
 имеет производную в некоторой точке
имеет производную в некоторой точке  , а функция
, а функция  имеет производную в точке
имеет производную в точке  . Тогда, сложная функция
. Тогда, сложная функция  имеет производную в точке
имеет производную в точке 

 .
. ,
,  , тогда
, тогда  . По теореме о производной сложной функции
. По теореме о производной сложной функции  ,
,  ,
,
 .
.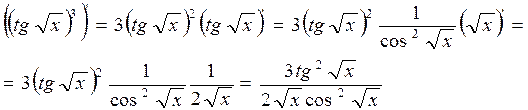
 .
.



