

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Решение СЛАУ с помощью надстройки Поиск решения
Похожие статьи вашей тематики
Пример 1.2: Найти решение СЛАУ из примера 1.1, используя надстройку Поиск решения.
При решении СЛАУ 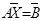 приложение Excel использует итерационные (приближенные) методы. Строится последовательность приближений приложение Excel использует итерационные (приближенные) методы. Строится последовательность приближений 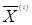 , i=0,1,…n. Назовем вектором невязок следующий вектор: , i=0,1,…n. Назовем вектором невязок следующий вектор:
 (1.9) (1.9)
Задача Excel заключается в том, чтобы найти такое приближение 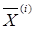 , при котором вектор невязок был бы нулевым, т.е. добиться совпадения значений правых и левых частей системы , при котором вектор невязок был бы нулевым, т.е. добиться совпадения значений правых и левых частей системы 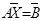 . .
Последовательность действий
1.
Возьмем новый лист (а можно и на том же). Заготовим таблицу, как показано на рис.1.2.
Рис.1.2.
2. Заготовим ячейки А7:С7, где будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например единицы. Эти значения можно рассматривать как нулевое приближение решения системы, 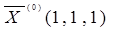 . .
3. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.
4. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейке D 3 введем и скопируем вниз до конца таблицы формулу: D3=СУММПРОИЗВ (A3:C3;$A$7:$C$7).
Используемая функция СУММПРОИЗВ принадлежит категории Математические.
5. В столбец Е запишем значения правых частей системы матрицу  . .
6.  В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы. В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
7. Будет не лишним проверить правильность вычислений для случая 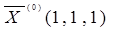 . .
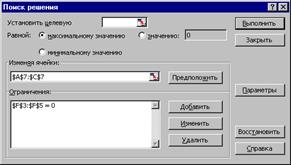
8. Зададим команду меню Сервис\Поиск решения. В окне Поиск решения (рис.1.3) в поле Изменяя ячейки укажем блок $А$7:$С$7, а в поле Ограничения – $F$3:$F$5 =0. Для этого надо щелкнуть на кнопке Добавить и ввести эти ограничения.
9. Щелкнем на кнопке Выполнить.
Рис. 1.3.
Полученное решение системы (1.8) х1 =1; х2 =-1 х3 =2 записано в ячейках А7:С7, рис.1.2.
Вопросы самоконтроля.
1) Как отделяются корни уравнения?
2) Как используется функция СУММПРОИЗВ?
3) Какой должна быть величина шага при отделении корней?
4) Какие условия должны быть выполнены для применения метода половинного деления отрезка?
Задания к лабораторным работам № 5-7
Найти решение данной системы
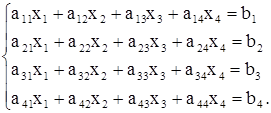
| № варианта
| Коэффициенты при неизвестных
| Свободные
члены
| 
| 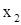
| 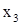
| 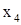
| |
|
|
|
|
|
| |
| 0,11270
| -2,39990
| 8,95146
| 0,75000
| 8,60527
| | 9,58778
| -3,45350
| 0,24300
| 1,46840
| 16,40216
| | 0,86400
| 4,23700
| -2,50200
| -1,72927
| -15,88846
| | -0,28427
| -4,58674
| -1,85970
| 0,14940
| 10,90588
| |
| 1,11270
| -3,02270
| -10,91328
| 1,06140
| 11,56420
| | 8,40446
| -3,45350
| 0,12430
| 0,84560
| 5,25400
| | -0,33640
| 5,11230
| -1,83880
| 16,03250
| -11,79026
| | -0,28427
| 5,85754
| -2,48250
| -0,16200
| -13,67224
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
| 1,42410
| -2,71130
| 9,60540
| 0,43860
| 6,30236
| | 0,33853
| -5,34326
| -2,17110
| -0,16200
| 12,83405
| | -0,02500
| 5,11230
| -2,46160
| -16,71758
| -11,58650
| | 8,40446
| -2,83070
| 0,43570
| 1,15700
| 15,77090
| |
| 0,28640
| 5,11230
| -2,15020
| 16,60758
| -12,52887
| | 0,80130
| -2,39990
| -8,29752
| 0,75000
| 7,078579
| | 8,52378
| -2,83070
| -0,18710
| 1,46840
| -2,20182
| | 0,33853
| 4,72046
| -1,85970
| -0,16200
| -11,78629
| |
| 0,11270
| -2,71130
| -9,60540
| 0,75000
| 8,93943
| | -8,99612
| -3,45350
| 0,12430
| 1,15700
| 1,07023
| | 0,02500
| 5,11230
| -2,15020
| 16,03250
| -11,77124
| | -0,28427
| 5,23474
| -2,17110
| -0,16200
| -12,58937
| |
| 0,80130
| -2,71130
| 9,60540
| 1,06140
| 6,16237
| | 8,52378
| -3,14210
| -0,18710
| 1,15700
| 16,18665
| | 0,02500
| 8,00900
| -1,83880
| -14,66234
| -10,15728
| | 0,02713
| -5,34326
| -2,17110
| -0,47340
| 14,18018
| |
| 0,86400
| 4,80090
| -2,46160
| 16,60758
| -12,88453
| | 1,42410
| -2,39990
| -8,95146
| 0,43860
| 6,53240
| | -10,17944
| -3,45350
| 0,3570
| 1,46840
| -0,61624
| | -0,28427
| 5,23474
| -1,85970
| -0,47340
| -12,05482
| |
| 0,80130
| -3,02270
| 9,60540
| 0,75000
| 5,53137
| | -0,28427
| -5,85754
| -2,48250
| -0,16200
| 15,60785
| | -0,33640
| 5,11230
| -2,15020
| -16,71758
| -13,11164
| | 8,52378
| -3,45350
| -0,18710
| 0,84560
| 15,88634
| |
| -0,33640
| 5,42370
| -2,46160
| -10,08774
| -14,95126
| | 1,42410
| -3,02270
| 10,25934
| 0,43860
| 4,97590
| | 8,99612
| -3,45350
| 0,43570
| 8,45600
| 15,15486
| | -0,28427
| -5,83234
| -2,48250
| 0,14940
| 13,79060
| |
| 8,01300
| -2,71130
| -8,95146
| 0,75000
| 9,11636
| | 0,28427
| 5,20954
| -2,17110
| 0,14940
| -13,29494
| | 0,02300
| 5,42370
| -2,15020
| 16,71758
| -10,78791
| | -9,11544
| -3,45350
| -0,18710
| 1,15700
| 1,72450
| |
| 1,42410
| -2,71130
| -10,25934
| 0,75000
| 9,42647
| | 0,33853
| 3,18060
| -2,17110
| 0,14940
| -11,34148
| | 0,02500
| 5,42370
| -2,50200
| 16,71758
| -9,13914
| | 8,40446
| -2,83070
| 0,43570
| 1,15700
| -2,82800
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
| 0,28640
| 5,42370
| -2,46160
| -17,97774
| -15,96309
| | 1,12700
| -2,39990
| 8,29752
| 0,43860
| 6,97586
| | 8,99612
| -3,14210
| 0,12430
| 1,46840
| 16,54115
| | 0,02713
| -4,07246
| -1,85970
| 0,14940
| 9,91665
| |
| 0,80130
| -3,02270
| -9,60540
| 0,75000
| 11,60641
| | 7,93212
| -3,14210
| -0,18710
| 0,84560
| 0,64655
| | -0,33640
| 5,42370
| -2,15020
| 17,40266
| -10,64578
| | 0,02713
| 5,31806
| -2,28250
| 0,14940
| -12,89141
| |
| 0,80130
| -2,39990
| 8,95146
| 1,06140
| 6,70370
| | 0,28427
| -5,23474
| -1,85970
| -0,47340
| 13,31273
| | 0,28640
| 4,80090
| -1,83800
| -15,23742
| -10,10485
| | 9,70710
| -3,45350
| -0,1871
| 1,46840
| 16,57743
| |
| 0,33640
| 4,80090
| -1,83880
| 15,34742
| -12,65950
| | 1,42410
| -3,02270
| 11,56722
| 1,06140
| 11,39202
| | -8,99612
| -3,45350
| 0,43570
| 0,84560
| 0,29410
| | -0,28427
| 6,48034
| -2,48250
| -0,47340
| -14,12547
| |
| 1,42410
| -2,39990
| 10,25934
| 1,06140
| 6,91312
| | 0,33853
| -5,34326
| -1,85970
| -0,47340
| 12,56925
| | 0,28640
| 4,80090
| -1,83880
| -15,23742
| -8,55119
| | 8,99612
| -2,83070
| 0,43570
| 1,46840
| 16,28011
| |
| 0,80130
| -2,39990
| 8,29752
| 0,75000
| 6,86659
| | 9,11544
| -3,14210
| -0,18710
| 1,46840
| 16,68709
| | 0,28640
| 4,80090
| -2,15020
| -15,92250
| -9,97026
| | 0,02713
| -4,72046
| -1,85970
| -0,47340
| 12,24497
| |
| 1,42410
| -3,02270
| -10,91328
| 0,75000
| 11,45227
| | -8,40446
| -3,14210
| 0,35700
| 8,45600
| -12,16038
| | -0,33640
| 8,00900
| -2,15020
| 16,03250
| -12,70757
| | 0,02713
| 5,96606
| -2,48250
| -0,73400
| -27,01020
| |
| 1,42410
| -2,39990
| 8,95146
| 0,43860
| 6,84369
| | 9,58778
| -3,14210
| 0,43570
| 1,46840
| 16,40812
| | 0,86400
| 5,11230
| -2,46160
| -17,29266
| -11,66944
| | 0,02713
| -4,09766
| -1,85970
| -0,16200
| 9,32315
| |
| 0,02500
| 4,80090
| -2,50200
| 15,34742
| -12,64048
| | 1,42410
| -2,11300
| -10,25934
| 0,75000
| 8,76250
| | -9,58778
| -3,45350
| 0,43570
| 1,15700
| -0,16016
| | -0,28427
| 5,85754
| -2,17110
| -0,47340
| -13,13770
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
| 0,28640
| 5,42370
| -1,83880
| 16,60758
| -9,22557
| | 1,42410
| -2,39990
| -10,25934
| 0,61400
| 6,77157
| | 10,17944
| -3,45350
| 0,43570
| 1,46840
| -0,16779
| | 0,28427
| 4,58674
| -1,85970
| 0,14940
| -10,62107
| |
| 1,42410
| -2,71130
| -9,13280
| 1,06140
| 9,36148
| | 8,99612
| -3,14210
| 0,35700
| 1,57000
| -1,40821
| | 0,25000
| 5,42870
| -1,83880
| 6,03250
| -9,30032
| | 0,02713
| 4,69526
| -2,17110
| 0,49400
| -10,27949
| |
| 1,42410
| -3,02270
| -11,56722
| 1,06140
| 2,15109
| | 0,38530
| 9,40860
| -2,48250
| 0,19400
| -12,32926
| | -0,33640
| 5,42370
| -1,83880
| 16,71758
| -9,25325
| | 8,12800
| -2,83070
| 0,35700
| 0,84560
| -2,28724
| |
| 0,80130
| -3,02270
| -10,25934
| 1,06140
| 11,73637
| | -0,28427
| 5,83234
| -2,48250
| 0,49400
| -14,47291
| | -0,33640
| 5,42370
| -1,83880
| 16,71758
| -10,80692
| | -8,52378
| -3,45350
| -0,18710
| 0,84560
| 2,17967
| |
| 0,80130
| -2,71130
| -8,29752
| 0,43860
| 9,08626
| | -8,52378
| -3,14210
| -0,18710
| 1,15700
| 0,10103
| | -0,02500
| 5,42370
| -2,46160
| 17,40266
| -10,62675
| | 0,02713
| 4,69526
| -2,17110
| 0,14940
| -11,71343
| |
| 0,28640
| 4,80090
| -1,83880
| 15,23742
| -13,39031
| | 1,11270
| -2,39990
| -9,60540
| 1,06140
| 6,73204
| | -8,99612
| -3,14210
| 0,12430
| 1,46840
| -1,25720
| | 0,02713
| 4,72046
| -1,85970
| -0,47340
| -11,35118
| |
| 0,80130
| -2,39990
| -7,64358
| 0,43860
| 6,89578
| | -0,28427
| 4,58674
| -1,85970
| 0,14940
| -12,02186
| | 0,26640
| 5,42370
| -2,46160
| 17,07774
| -10,64711
| | -9,70710
| 3,45350
| -0,18710
| 1,46840
| 1,26392
| |
| -0,33640
| 4,80090
| -2,46160
| -16,71758
| -8,98045
| | 1,11270
| -3,02270
| 9,60540
| 0,43860
| 5,41943
| | 7,81280
| -3,14210
| 0,12430
| 0,84560
| 14,99671
| | 0,02713
| -5,96606
| -2,48250
| -0,47340
| 15,29948
| |
| 1,11270
| -2,71130
| 8,95146
| 0,43860
| 6,06062
| | 8,99612
| -3,45350
| 0,12430
| 1,15700
| 15,49607
| | -0,02500
| 4,80090
| -2,46160
| -16,03250
| -9,14355
| | -0,28427
| -5,85754
| -2,17110
| -0,47340
| 14,35349
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
| 1,42410
| -3,02270
| 11,56722
| 1,06140
| 4,74101
| | 8,40446
| -3,14210
| 0,43570
| 0,84560
| 15,12192
| | -0,33640
| 5,11230
| -1,83880
| -16,03250
| 11,68307
| | 0,02713
| -5,34326
| -2,48250
| -0,16200
| 12,90826
| |
| 0,33640
| 5,11230
| -2,15020
| 16,71758
| -11,73373
| | 0, 11270
| -3,02270
| -10,25934
| 0,75000
| 11,52934
| | 7,81280
| -3,14210
| 0,24300
| 0,84560
| 0,05805
| | 0,02713
| 5,34326
| -2,48250
| -0,16200
| -12,16925
| |
| 0,02500
| 4,80090
| -2,15020
| -15,34742
| -10,02268
| | 0,80130
| -2,71130
| 8,95146
| 0,75000
| 6,42511
| | 7,93212
| -2,83070
| -0,18710
| 1,15700
| 16,02528
| | 0,33853
| -5,96606
| -2,17110
| -0,73400
| 16,13629
| |
| 1,11270
| -2,39990
| -8,29752
| 0,43860
| 6,71409
| | -9,58778
| -3,45350
| 0,12430
| 1,46840
| 0,61506
| | 0,26400
| 5,11230
| -2,46160
| 17,29266
| -11,82287
| | -0,28427
| 4,61194
| -1,85970
| -0,16200
| -11,41139
| |
| 1,11270
| -3,02270
| 10,25934
| 0,75000
| 5,00928
| | 8,40446
| -3,45350
| 0,12430
| 0,84560
| 15,03841
| | -0,33640
| 4,80090
| -2,15020
| -16,03250
| -9,11502
| | -0,28427
| -6,48034
| -2,48250
| -0,47340
| 6,28870
| |
| -0,02500
| 5,11230
| -2,46150
| 16,71758
| -11,71470
| | 1,11270
| -2,71130
| -8,95146
| 0,43860
| 9,00442
| | -8,40446
| -3,14210
| 0,12430
| 1,15700
| -0,48746
| | 0,02713
| 4,72046
| -2,17110
| -0,16200
| -11,08638
| |
| -0,33640
| 5,42370
| -1,83880
| -16,71758
| -15,78430
| | 1,11270
| -3,02270
| 9,13280
| 1,06140
| 5,26310
| | 7,81280
| -3,14210
| 0,12430
| 0,84560
| 15,25495
| | 0,02713
| -5,31806
| -2,48250
| 0,14940
| 13,69198
| |
| 0,25000
| 5,42370
| -2,15020
| -16,71758
| -15,71771
| | 1,11270
| -2,71130
| 9,60540
| 0,75000
| 6,31920
| | 8,40446
| -3,14210
| 0,12430
| 1,15700
| 15,89804
| | 0,02713
| -4,69526
| -2,17110
| 0,14940
| 11,75676
| |
| 1,11270
| -2,71130
| 2,59340
| 1,06140
| 6,10400
| | 8,99612
| -3,45350
| 0,12430
| 1,57000
| 15,84940
| | -0,02500
| 5,42370
| -1,83880
| -16,03250
| -15,64308
| | -0,84270
| -2,09540
| -2,17110
| 0,14940
| 12,74599
| Лабораторная работа 6. Итерационные методы решения систем линейных уравнений
Цель: Ознакомиться с итерационными методами решения систем линейных уравнений и их реализацией в MS Excel.
Задание: Решить систему линейных уравнений с точностью ε одним из методов:
1) Якоби, e = 10–3;
Алгоритмы методов и их реализация в ms excel
Метод якоби
Алгоритм
1. Выписать для системы 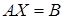 матрицу коэффициентов матрицу коэффициентов 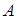 и вектор правой части и вектор правой части 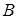 . .
2. Преобразовать исходную систему к виду  , где элементы матрицы , где элементы матрицы  определяются по формулам: определяются по формулам:
 , ,
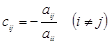 , ,
элементы столбца 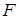 : :
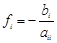 . .
3. Проверить условие сходимости: имеет ли матрица 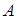 диагональное преобладание или в преобразованной системе уравнений диагональное преобладание или в преобразованной системе уравнений  имеет ли норма матрицы коэффициентов значение, меньшее единицы имеет ли норма матрицы коэффициентов значение, меньшее единицы 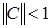 (в качестве нормы можно взять евклидову норму (в качестве нормы можно взять евклидову норму 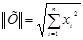 ). ).
5. Задать вектор нулевого приближения 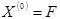 . .
6. Вычислить координаты вектора следующего, более точного приближения к решению по итерационной формуле:
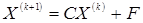
или
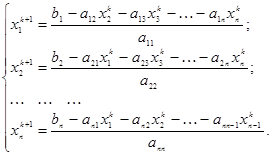
7. Окончание итерационного процесса:
оценить погрешность 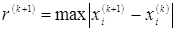 ; ;
итерационный процесс заканчивается, как только 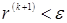 . .
Реализация в MS Excel
1.Решить систему линейных алгебраических уравнений:
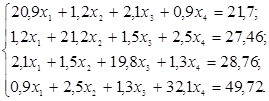
8. Расположить на листе исходные данные:
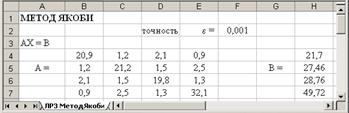
9. Рассчитать элементы матрицы 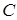 и столбца и столбца 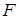 : :
Вид рабочего листа с результатом расчета
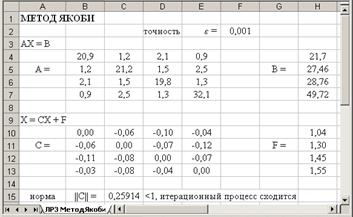
Вид рабочего листа с формулами
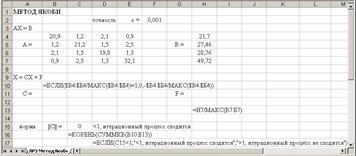
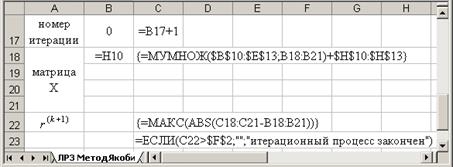
10. Уточнение корней системы линейных уравнений методом Якоби с помощью таблицы вычислений (в качестве начального приближения выбрать значения столбца 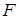 ): ):
Вид рабочего листа с результатом расчета
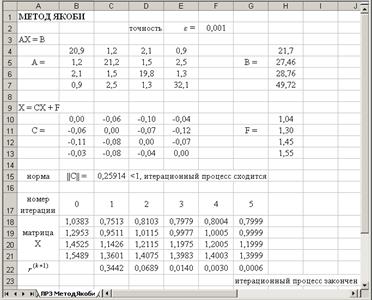
Вид рабочего листа с формулами
Примечание: Фигурные скобки означают, что соответствующая формула выводится массивом, т. е. с использованием комбинации Ctrl + Shift + Enter.
Уточнение корня с использованием режима Итерации MS Excel (вручную):
создать копию листа: Правка – Переместить/Скопировать лист…, на которой удалить ячейки с итерационным процессом:
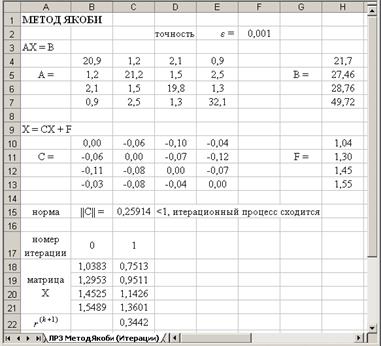
настроить MS Excel на выполнение итераций вручную: Сервис – Параметры – Вычисления – вручную; итерации разрешить, Предельное число итераций – 1, Относительная погрешность – 0,001;
организовать в таблице циклические ссылки: в ячейках, где хранились старые значения корней, поставить ссылку на ячейки, где рассчитаны новые, более точные значения корней:
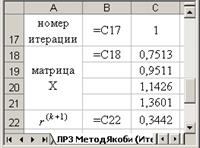
нажимать клавишу F9, наблюдая за поведением погрешности:
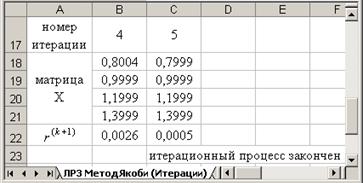
После окончания вычислительного процесса выполнить: Сервис – Параметры – Вычисления и вернуть предустановленные настройки.
Лабораторная работа 7. Итерационные методы решения систем линейных уравнений
Цель: Ознакомиться с итерационными методами решения систем линейных уравнений и их реализацией в MS Excel.
Задание: Решить систему линейных уравнений с точностью ε одним из методов:
1) Зейделя, e = 10–6;
Алгоритм
Выписать для системы 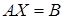 матрицу коэффициентов матрицу коэффициентов 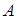 и вектор правой части и вектор правой части 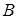 . .
Преобразовать исходную систему к виду  , где элементы матрицы , где элементы матрицы 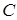 определяются по формулам: определяются по формулам:
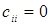 , ,
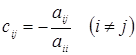 , ,
элементы столбца  : :
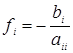 . .
Проверить условие сходимости: имеет ли матрица 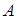 диагональное преобладание или в преобразованной системе уравнений диагональное преобладание или в преобразованной системе уравнений  имеет ли норма матрицы коэффициентов значение, меньшее единицы имеет ли норма матрицы коэффициентов значение, меньшее единицы 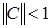 (в качестве нормы можно взять евклидову норму (в качестве нормы можно взять евклидову норму 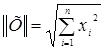 ). ).
Задать вектор нулевого приближения 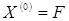 . .
Вычислить координаты вектора следующего, более точного приближения к решению по итерационным формулам:
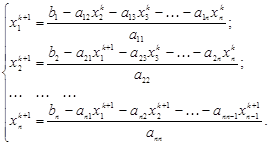
Окончание итерационного процесса:
оценить погрешность 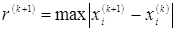 ; ;
итерационный процесс заканчивается, как только 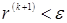 . .
Реализация в MS Excel
Расположить на листе исходные данные и уточнить корни системы линейных уравнений методом Зейделя с помощью таблицы вычислений (в качестве начального приближения выбрать значения столбца F):
Вид рабочего листа с результатом расчета
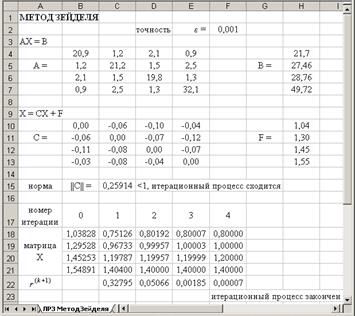
Вид рабочего листа с формулами
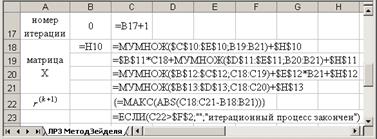
Уточнение корня с использованием режима Итерации MS Excel (вручную):
создать копию листа: Правка – Переместить/Скопировать лист…, на которой удалить ячейки с итерационным процессом:
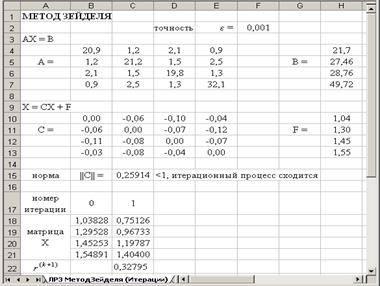
настроить MS Excel на выполнение итераций вручную: Сервис – Параметры – Вычисления – вручную; итерации разрешить, Предельное число итераций – 1, Относительная погрешность – 0,001;
организовать в таблице циклические ссылки: в ячейках, где хранились старые значения корней, поставить ссылку на ячейки, где рассчитаны новые, более точные значения корней:

нажимать клавишу F9, наблюдая за поведением погрешности:
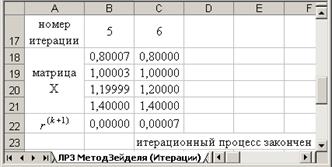
После окончания вычислительного процесса выполнить: Сервис – Параметры – Вычисления и вернуть предустановленные настройки.
Поскольку подсчет номера итерации и расчет погрешности работают некорректно, следует модифицировать формулы:
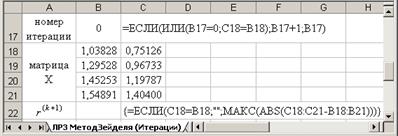
и снова провести расчет:
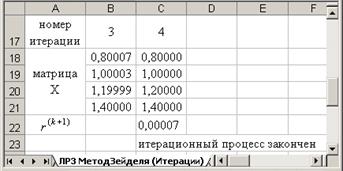
После окончания вычислительного процесса выполнить: Сервис – Параметры – Вычисления и вернуть предустановленные настройки.
Лабораторная работа 8. Теория приближений функций
Цель: Ознакомиться с численными методами получения аналитической зависимости по экспериментальным точкам и их реализацией в MS Excel.
Задание:
1) Найти приближенное значение функции при заданном значении аргумента  с помощью интерполяционного полинома Лагранжа, если функция задана в не равноотстоящих узлах; с помощью интерполяционного полинома Лагранжа, если функция задана в не равноотстоящих узлах; 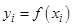 , , 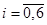 ; ; 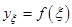 ; ; 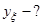
2) Оценить погрешность полученного значения.
Вопросы самоконтроля.
1) Постановка задачи интерполирования. Геометрическая иллюстрация.
2) В чем различие между задачами интерполяции и задачами экстраполяции?
3) Привести формулу Лагранжа. Дать оценку погрешности.
4) Как выглядит формула Лагранжа для равностоящих узлов?
5) От чего зависит точность получаемого формулой Лагранжа результата?
6) Когда полином 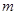 порядка будет аппроксимирован формулой Лагранжа с наименьшей погрешностью? порядка будет аппроксимирован формулой Лагранжа с наименьшей погрешностью?
|
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 1,0000
| 6,0100
| 0,2955
| 0,8253
| 0,9553
| 0,1011
| 3,6788
| 0,9689
| 0,9044
| 0,1011
| 3,6788
| |
| 1,1000
| 6,9066
| 0,4259
| 0,8162
| 0,9460
| 0,1076
| 3,6616
| 1,0587
| 0,9513
| 0,1183
| 4,0277
| |
| 1,2320
| 8,3884
| 0,6095
| 0,8110
| 0,9325
| 0,1154
| 3,5938
| 1,1740
| 0,9900
| 0,1421
| 4,4276
| 
| 1,4796
| 12,1761
| 0,9142
| 0,8231
| 0,9031
| 0,1279
| 3,3694
| 1,3796
| 0,9813
| 0,1893
| 4,9855
| |
| 1,9383
| 23,2239
| 0,6753
| 0,9067
| 0,8356
| 0,1453
| 2,7901
| 1,7152
| 0,6555
| 0,2816
| 5,4082
| |
| 1,9577
| 23,8200
| 0,6283
| 0,9112
| 0,8324
| 0,1459
| 2,7639
| 1,7279
| 0,6332
| 0,2856
| 5,4110
| |
| 2,0380
| 26,4092
| 0,4031
| 0,9299
| 0,8189
| 0,1483
| 2,6553
| 1,7791
| 0,5343
| 0,3021
| 5,4115
| 
| 1,3
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 1,8545
| 20,7751
| 0,7277
| 0,8875
| 0,8492
| 0,1426
| 2,9028
| 1,6588
| 0,9243
| 0,2644
| 3,2300
| |
| 1,5022
| 12,5914
| 0,9769
| 0,8256
| 0,9002
| 0,1289
| 3,3445
| 1,3975
| 0,7538
| 0,1937
| 3,0144
| |
| 1,1732
| 7,6850
| 0,6229
| 0,8123
| 0,9387
| 0,1120
| 3,6296
| 1,1231
| 0,7000
| 0,1314
| 2,5550
| 
| 0,8330
| 4,9104
| 0,1928
| 0,8497
| 0,9689
| 0,0891
| 3,6214
| 0,8150
| 0,7411
| 0,0742
| 1,8099
| |
| 0,5589
| 4,0517
| -0,0230
| 0,9073
| 0,9860
| 0,0656
| 3,1961
| 0,5535
| 0,8178
| 0,0367
| 1,0718
| |
| 0,3354
| 4,0715
| -0,0886
| 0,9581
| 0,9949
| 0,0426
| 2,3981
| 0,3342
| 0,8918
| 0,0143
| 0,4825
| |
| 0,1948
| 4,3493
| -0,0789
| 0,9839
| 0,9983
| 0,0260
| 1,6035
| 0,1946
| 0,9386
| 0,0051
| 0,1875
| 
| 0,3
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 0,2143
| 4,3002
| -0,0826
| 0,9809
| 0,9979
| 0,0284
| 1,7298
| 0,2140
| 0,9548
| 0,0061
| 1,8888
| |
| 0,2572
| 4,2037
| -0,0881
| 0,9735
| 0,9970
| 0,0335
| 1,9887
| 0,2567
| 0,9453
| 0,0086
| 1,8466
| |
| 0,3269
| 4,0830
| -0,0892
| 0,9599
| 0,9952
| 0,0416
| 2,3574
| 0,3258
| 0,9297
| 0,0136
| 1,7688
| 
| 0,4282
| 3,9946
| -0,0735
| 0,9377
| 0,9918
| 0,0526
| 2,7906
| 0,4258
| 0,9071
| 0,0225
| 1,6415
| |
| 0,5657
| 4,0603
| -0,0194
| 0,9057
| 0,9856
| 0,0663
| 3,2129
| 0,5600
| 0,8771
| 0,0375
| 1,4547
| |
| 0,7756
| 4,6388
| 0,1357
| 0,8603
| 0,9731
| 0,0845
| 3,5710
| 0,7610
| 0,8366
| 0,0656
| 1,1691
| |
| 1,0935
| 6,8430
| 0,5139
| 0,8167
| 0,9467
| 0,1072
| 3,6637
| 1,0529
| 0,8014
| 0,1172
| 0,7981
| 
| 0,25
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 1,0000
| 3,1000
| 1,9320
| 2,1700
| 0,9553
| 0,1011
| 3,6788
| 0,9689
| 0,9636
| 0,1011
| 3,6788
| |
| 1,1000
| 3,0131
| 2,0891
| 1,9868
| 0,9460
| 0,1076
| 3,6616
| 1,0587
| 0,9942
| 0,1183
| 4,0277
| |
| 1,2320
| 2,8473
| 2,2090
| 1,7349
| 0,9325
| 0,1154
| 3,5938
| 1,1740
| 0,9932
| 0,1421
| 4,4276
| 
| 1,3922
| 2,5701
| 2,1119
| 1,4382
| 0,9140
| 0,1238
| 3,4600
| 1,3087
| 0,9200
| 0,1723
| 4,8169
| |
| 1,5871
| 2,1234
| 1,4772
| 1,1459
| 0,8888
| 0,1326
| 3,2459
| 1,4638
| 0,7166
| 0,2104
| 5,1515
| |
| 1,8251
| 1,4212
| 0,0390
| 1,0001
| 0,8538
| 0,1416
| 2,9421
| 1,6384
| 0,3119
| 0,2584
| 5,3696
| |
| 2,1171
| 0,3358
| -1,0777
| 1,2810
| 0,8050
| 0,1504
| 2,5485
| 1,8274
| -0,3148
| 0,3185
| 5,3956
| 
| 1,7
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 2,3289
| 7,4025
| 4,1063
| 0,7875
| 0,7657
| 0,1556
| 2,2685
| 1,9452
| 1,2182
| 0,3624
| 3,1698
| |
| 2,2147
| 7,9204
| 3,2178
| 0,4896
| 0,7873
| 0,1529
| 2,4181
| 1,8838
| 1,1554
| 0,3387
| 3,2133
| |
| 2,0597
| 8,5681
| 2,9438
| 0,1833
| 0,8151
| 0,1489
| 2,6259
| 1,7926
| 1,0569
| 0,3066
| 3,2452
| 
| 1,8537
| 9,3255
| 3,8554
| 0,0038
| 0,8493
| 0,1426
| 2,9039
| 1,6582
| 0,9238
| 0,2643
| 3,2298
| |
| 1,6128
| 10,0558
| 5,3489
| 0,1169
| 0,8852
| 0,1337
| 3,2148
| 1,4834
| 0,7958
| 0,2156
| 3,1108
| |
| 1,3708
| 10,6117
| 6,1447
| 0,4758
| 0,9166
| 0,1227
| 3,4805
| 1,2911
| 0,7196
| 0,1682
| 2,8627
| |
| 1,1104
| 11,0022
| 6,1029
| 0,9672
| 0,9450
| 0,1082
| 3,6580
| 1,0679
| 0,7012
| 0,1202
| 2,4370
| 
| 2,1
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 1,2214
| 16,7391
| 8,1582
| 0,7551
| 0,9336
| 0,1148
| 3,6009
| 1,1649
| 0,8010
| 0,1402
| 0,6805
| |
| 1,3802
| 18,0820
| 8,3779
| 0,4592
| 0,9155
| 0,1232
| 3,4716
| 1,2989
| 0,8143
| 0,1700
| 0,5626
| |
| 1,5872
| 20,0003
| 8,2815
| 0,1457
| 0,8888
| 0,1326
| 3,2457
| 1,4639
| 0,8567
| 0,2105
| 0,4545
| 
| 1,8571
| 22,7888
| 7,1194
| 0,0045
| 0,8488
| 0,1427
| 2,8994
| 1,6605
| 0,9505
| 0,2650
| 0,3847
| |
| 2,2099
| 26,9367
| 4,8706
| 0,4782
| 0,7882
| 0,1528
| 2,4245
| 1,8811
| 1,1017
| 0,3377
| 0,3926
| |
| 2,6740
| 33,2783
| 7,8721
| 1,7323
| 0,6951
| 0,1623
| 1,8444
| 2,0984
| 1,1989
| 0,4341
| 0,5204
| |
| 3,2890
| 43,2810
| 4,7946
| 1,2357
| 0,5514
| 0,1711
| 1,2265
| 2,2384
| 0,9503
| 0,5629
| 0,7898
| 
|
|
|
|
|
|
|
|
|
|
|
|
|



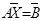 приложение Excel использует итерационные (приближенные) методы. Строится последовательность приближений
приложение Excel использует итерационные (приближенные) методы. Строится последовательность приближений 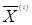 , i=0,1,…n. Назовем вектором невязок следующий вектор:
, i=0,1,…n. Назовем вектором невязок следующий вектор: (1.9)
(1.9)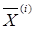 , при котором вектор невязок был бы нулевым, т.е. добиться совпадения значений правых и левых частей системы
, при котором вектор невязок был бы нулевым, т.е. добиться совпадения значений правых и левых частей системы 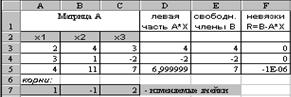
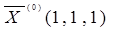 .
. .
. В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
В столбец F введем невязки в соответствии с формулой (1.9), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.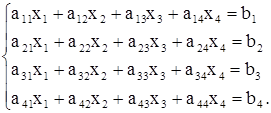

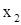
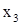
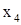
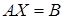 матрицу коэффициентов
матрицу коэффициентов 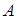 и вектор правой части
и вектор правой части 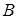 .
. , где элементы матрицы
, где элементы матрицы 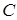 определяются по формулам:
определяются по формулам: ,
,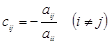 ,
,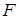 :
: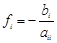 .
.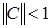 (в качестве нормы можно взять евклидову норму
(в качестве нормы можно взять евклидову норму 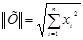 ).
).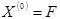 .
.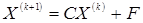
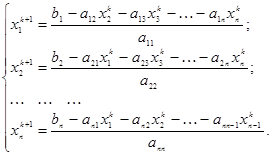
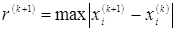 ;
;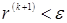 .
.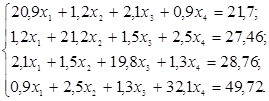








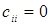 ,
,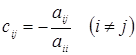 ,
,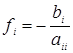 .
.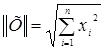 ).
).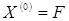 .
.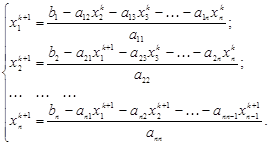







 с помощью интерполяционного полинома Лагранжа, если функция задана в не равноотстоящих узлах;
с помощью интерполяционного полинома Лагранжа, если функция задана в не равноотстоящих узлах; 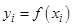 ,
, 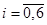 ;
; 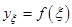 ;
; 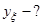
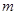 порядка будет аппроксимирован формулой Лагранжа с наименьшей погрешностью?
порядка будет аппроксимирован формулой Лагранжа с наименьшей погрешностью?



