
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец выполнения лабораторной работы № 2Содержание книги
Поиск на нашем сайте
(Решение нелинейных уравнений. Метод итерации.)
Постановка задачи. Найти корень нелинейного уравнения Решение задачи. Отделим корень уравнения на отрезке
Выделим отрезок Получим равносильное уравнению
При таком выборе функция Тогда получим следующее значение Если свести результаты в таблицу получим
Приближенное решение Следовательно, приближенное значение корня равно Запишем приближенное значение корня только верными значащими цифрами в узком смысле. Имеем Найдем число верных знаков для Ответ:
Лабораторная работа №5. Решение систем линейных алгебраических уравнений. Прямые методы. Метод Гаусса Цель: Ознакомиться с численными методами решения систем линейных уравнений и их реализацией в MS Excel. Теоретические сведения
Дана система n линейных уравнений с n неизвестными
Если система имеет единственное решение, то значения Наиболее распространенным является метод Гаусса, согласно которому путем последовательного исключения неизвестных система (1) приводится к треугольному виду:
Приведение матрицы системы к виду (2) называется прямым ходом. Вычисление неизвестных – обратным ходом. Необходимость округлять в промежуточных вычислениях приводит к тому, что возникает очень большая погрешность округления, искажающая результат. Существует несколько видов вычислительных схем метода Гаусса, в различной степени уменьшающих погрешность округления. Наиболее эффективной является “схема с выбором главного элемента”.
Прямой ход Исключение неизвестных в прямом ходе осуществляется по этапам. На каждом i-м этапе (i=1, 2, …, n) среди коэффициентов при неизвестном выбираем наибольший по абсолютной величине – “главный элемент”. Строка, его содержащая, называется главной. Затем главную строку прибавляем ко всем остальным строкам, предварительно умножив ее на специально подобранные числа Главная строка i-го этапа в дальнейших преобразованиях не участвует, поэтому для приведения системы (1) к виду (2) нужно проделать
Обратный ход Вначале из уравнения в последней строке находится
Контроль и точность вычислений Для проверки расчета полезно найти невязки
Если они велики, то это означает грубую ошибку в расчете.
Контроль прямого хода совершается с помощью
При прямом ходе над контрольными суммами
Контроль обратного хода. В треугольную матрицу, подготовленную для обратного хода, вместо столбца свободных членов подставляем столбец контрольных сумм и выполняем обратный ход. При этом будут найдены значения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.76.201 (0.008 с.) |

 методом итерации с точностью
методом итерации с точностью 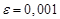 .
.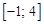 графическим методом. Для этого табулируем функцию
графическим методом. Для этого табулируем функцию  на данном отрезке.
на данном отрезке.
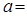

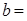


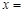
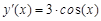
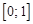 , где находится корень, и уточним его методом итерации.
, где находится корень, и уточним его методом итерации.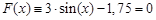 уравнение
уравнение  . Функцию
. Функцию  будем искать в виде
будем искать в виде  , где
, где  .
.

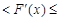
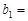

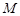 ,
,


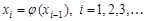 ,
,  , где
, где  .
. , условие остановки итерационной последовательности
, условие остановки итерационной последовательности 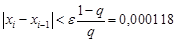 , при выборе приближенного решения
, при выборе приближенного решения  с погрешностью приближенного решения
с погрешностью приближенного решения  .
.

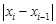









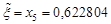 , погрешность
, погрешность  , число итераций
, число итераций  .
. .
. ,
, 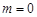 ,
, 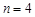 . Округлим
. Округлим  до
до  ,
, 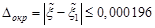 ,
,  .
. ,
, 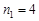 . Так как
. Так как 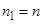 , то получим приближенное значение корня с числом верных знаков
, то получим приближенное значение корня с числом верных знаков 
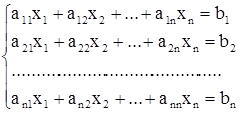 (1)
(1)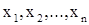 могут быть найдены по известным формулам Крамера, но этот способ неудобен и приходится применять приближенные или численные методы решения.
могут быть найдены по известным формулам Крамера, но этот способ неудобен и приходится применять приближенные или численные методы решения.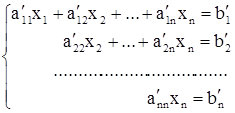 (2)
(2)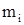 так, чтобы коэффициенты при
так, чтобы коэффициенты при 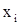 во всех строках, кроме главной, обратились бы в нуль.
во всех строках, кроме главной, обратились бы в нуль.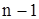 исключение неизвестных.
исключение неизвестных.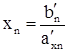 , затем это значение подставляется в предыдущее главное уравнение, которое разрешается относительно
, затем это значение подставляется в предыдущее главное уравнение, которое разрешается относительно 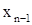 , и т.д.
, и т.д. .
. контрольных сумм. У исходной матрицы системы находят сумму всех элементов i-ой строки и соответствующего свободного члена
контрольных сумм. У исходной матрицы системы находят сумму всех элементов i-ой строки и соответствующего свободного члена .
. производятся те же действия, что и над другими элементами матрицы. При отсутствии случайных ошибок контрольные суммы, найденные на каждом этапе, должны совпадать в пределах погрешности округления с аналогичными строчными суммами
производятся те же действия, что и над другими элементами матрицы. При отсутствии случайных ошибок контрольные суммы, найденные на каждом этапе, должны совпадать в пределах погрешности округления с аналогичными строчными суммами  . Если это условие нарушено, то при вычислении i-й строки допущена ошибка.
. Если это условие нарушено, то при вычислении i-й строки допущена ошибка.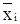 . Если
. Если  , то обратный ход совершен верно.
, то обратный ход совершен верно.


