

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Образец выполнения лабораторной работы №12
(Приближенное решение ОДУ. Задача Коши.)
Пример. Найти приближенное решение задачи Коши для обыкновенного уравнения первого порядка методом Эйлера и методом Эйлера с уточнением с шагом  : :
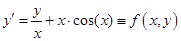 , , 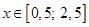 , ,  . .
1) По методу Эйлера приближенное решение ищется по схеме
 , ,  . . 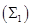
По данной схеме составим таблицу значений
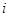
| 
| 
| 
| 
| 
| |
| 0,5
| 0,918217
| 0,239713
| 0,239713
| 1,515452
| |
| 0,55
| 0,988204
| 0,285624
| 0,287478
| 1,417571
| |
| 0,6
| 1,053591
| 0,335034
| 0,338785
| 1,311886
| |
| 0,65
| 1,113937
| 0,387713
| 0,393371
| 1,198796
| |
| 0,7
| 1,168833
| 0,44341
| 0,450952
| 1,078732
| |
| 0,75
| 1,217902
| 0,501852
| 0,511229
| 0,952149
| |
| 0,8
| 1,260799
| 0,562747
| 0,573885
| 0,819529
| |
| 0,85
| 1,297206
| 0,625787
| 0,638588
| 0,681378
| |
| 0,9
| 1,326835
| 0,690647
| 0,704994
| 0,538226
| |
| 0,95
| 1,349429
| 0,756989
| 0,772745
| 0,390621
| |
|
| 1,364763
| 0,82446
| 0,841471
| 0,239134
| |
| 1,05
| 1,372639
| 0,892699
| 0,910794
| 0,084348
| |
| 1,1
| 1,372893
| 0,96133
| 0,980328
| 0,073136
| |
| 1,15
| 1,365391
| 1,029975
| 1,049679
| 0,232704
| |
| 1,2
| 1,350033
| 1,098245
| 1,118447
| 0,393731
| |
| 1,25
| 1,32675
| 1,165746
| 1,186231
| 0,555586
| |
| 1,3
| 1,295505
| 1,232084
| 1,252626
| 0,717628
| |
| 1,35
| 1,256295
| 1,296859
| 1,317227
| 0,879213
| |
| 1,4
| 1,20915
| 1,359674
| 1,37963
| 1,039695
| |
| 1,45
| 1,15413
| 1,420131
| 1,439434
| 1,198428
| |
| 1,5
| 1,091331
| 1,477838
| 1,496242
| 1,354768
| |
| 1,55
| 1,02088
| 1,532404
| 1,549665
| 1,508075
| |
| 1,6
| 0,942936
| 1,583448
| 1,599318
| 1,657717
| |
| 1,65
| 0,85769
| 1,630595
| 1,644827
| 1,803069
| |
| 1,7
| 0,765364
| 1,67348
| 1,68583
| 1,943519
| |
| 1,75
| 0,666211
| 1,711748
| 1,721975
| 2,078468
| |
| 1,8
| 0,560513
| 1,745058
| 1,752926
| 2,207330
| |
| 1,85
| 0,448582
| 1,773084
| 1,778359
| 2,329540
| |
| 1,9
| 0,330757
| 1,795513
| 1,79797
| 2,444549
| |
| 1,95
| 0,207404
| 1,812051
| 1,811471
| 2,551833
| |
|
| 0,078917
| 1,822421
| 1,818595
| 2,650889
| |
| 2,05
| -0,05429
| 1,826367
| 1,819093
| 2,741238
| |
| 2,1
| -0,19177
| 1,823653
| 1,81274
| 2,822432
| |
| 2,15
| -0,33307
| 1,814064
| 1,799332
| 2,894048
| |
| 2,2
| -0,4777
| 1,797411
| 1,778692
| 2,955694
| |
| 2,25
| -0,62516
| 1,773526
| 1,750665
| 3,007012
| |
| 2,3
| -0,77493
| 1,742268
| 1,715122
| 3,047674
| |
| 2,35
| -0,92647
| 1,703522
| 1,671962
| 3,077389
| |
| 2,4
| -1,07925
| 1,657198
| 1,621112
| 3,095899
| |
| 2,45
| -1,23268
| 1,603236
| 1,562524
| 3,102986
| |
| 2,5
| -1,38622
| 1,541601
| 1,49618
| 3,098468
|
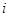
| 
| 
| 
| 
| 
| |
| 0,5
|
|
|
|
| |
| 0,55
| 0,001894
| 0,66%
| 0,00185
| 0,65%
| |
| 0,6
| 0,003666
| 1,08%
| 0,00375
| 1,11%
| |
| 0,65
| 0,005306
| 1,35%
| 0,00566
| 1,44%
| |
| 0,7
| 0,006805
| 1,51%
| 0,00754
| 1,67%
| |
| 0,75
| 0,008153
| 1,59%
| 0,00938
| 1,83%
| |
| 0,8
| 0,009343
| 1,63%
| 0,01114
| 1,94%
| |
| 0,85
| 0,010368
| 1,62%
| 0,01280
| 2,00%
| |
| 0,9
| 0,011219
| 1,59%
| 0,01435
| 2,04%
| |
| 0,95
| 0,011892
| 1,54%
| 0,01576
| 2,04%
| |
|
| 0,012380
| 1,47%
| 0,01701
| 2,02%
| |
| 1,05
| 0,012679
| 1,39%
| 0,01810
| 1,99%
| |
| 1,1
| 0,012785
| 1,30%
| 0,01900
| 1,94%
| |
| 1,15
| 0,013076
| 1,25%
| 0,01970
| 1,88%
| |
| 1,2
| 0,013568
| 1,21%
| 0,02020
| 1,81%
| |
| 1,25
| 0,014262
| 1,20%
| 0,02048
| 1,73%
| |
| 1,3
| 0,015159
| 1,21%
| 0,02054
| 1,64%
| |
| 1,35
| 0,016258
| 1,23%
| 0,02037
| 1,55%
| |
| 1,4
| 0,017558
| 1,27%
| 0,01996
| 1,45%
| |
| 1,45
| 0,019056
| 1,32%
| 0,01930
| 1,34%
| |
| 1,5
| 0,020749
| 1,39%
| 0,01840
| 1,23%
| |
| 1,55
| 0,022635
| 1,46%
| 0,01726
| 1,11%
| |
| 1,6
| 0,024707
| 1,54%
| 0,01587
| 0,99%
| |
| 1,65
| 0,026961
| 1,64%
| 0,01423
| 0,87%
| |
| 1,7
| 0,029390
| 1,74%
| 0,01235
| 0,73%
| |
| 1,75
| 0,031988
| 1,86%
| 0,01023
| 0,59%
| |
| 1,8
| 0,034747
| 1,98%
| 0,00787
| 0,45%
| |
| 1,85
| 0,037659
| 2,12%
| 0,00528
| 0,30%
| |
| 1,9
| 0,040715
| 2,26%
| 0,00246
| 0,14%
| |
| 1,95
| 0,043905
| 2,42%
| 0,00058
| 0,03%
| |
|
| 0,047218
| 2,60%
| 0,00383
| 0,21%
| |
| 2,05
| 0,050645
| 2,78%
| 0,00727
| 0,40%
| |
| 2,1
| 0,054173
| 2,99%
| 0,01091
| 0,60%
| |
| 2,15
| 0,057790
| 3,21%
| 0,01473
| 0,82%
| |
| 2,2
| 0,061485
| 3,46%
| 0,01872
| 1,05%
| |
| 2,25
| 0,065244
| 3,73%
| 0,02286
| 1,31%
| |
| 2,3
| 0,069053
| 4,03%
| 0,02715
| 1,58%
| |
| 2,35
| 0,072900
| 4,36%
| 0,03156
| 1,89%
| |
| 2,4
| 0,076770
| 4,74%
| 0,03609
| 2,23%
| |
| 2,45
| 0,080649
| 5,16%
| 0,04071
| 2,61%
| |
| 2,5
| 0,084527
| 5,65%
| 0,04542
| 3,04%
|
Где  -абсолютная погрешность нахождения -абсолютная погрешность нахождения  определяемая следующим образом: определяемая следующим образом:  , ,  . Используя исходное уравнение, . Используя исходное уравнение,
получим  . .
В таблице  , , 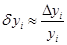  абсолютная и относительная погрешности приближенного значения абсолютная и относительная погрешности приближенного значения  . .
Для сравнения погрешностей найдем погрешность по отношению к точному значению искомой функции:  , ,  , ,
И построим графики точных и приближенных значений функции  , а так же графики абсолютных погрешностей (где , а так же графики абсолютных погрешностей (где  соответствует погрешности соответствует погрешности  , а , а  - погрешности - погрешности  ). ).
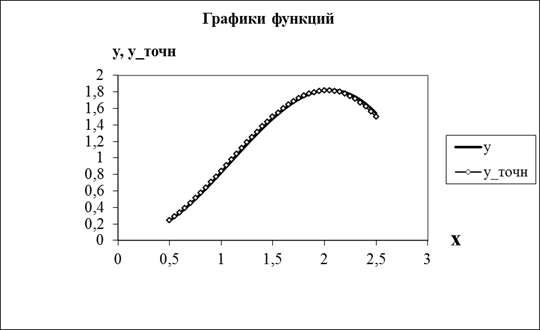
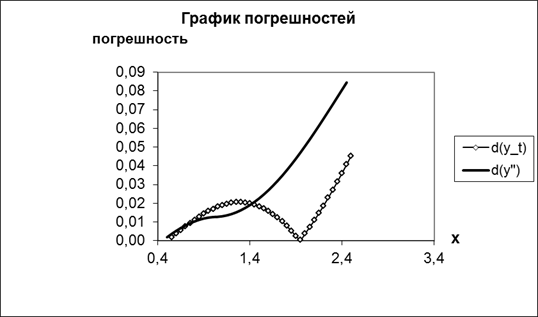
Вывод. Из полученных приближенных значений и графиков следует, что метод Эйлера позволяет хорошо описать искомую функцию на качественном уровне, но дает достаточно большую погрешность численных значений. Поэтому метод Эйлера может быть использован при качественной оценке решения искомой функции, а для нахождения численных значений можно использовать более точные методы.
P.S. Характерный изгиб графика  можно объяснить изменением вклада можно объяснить изменением вклада  в величину погрешности. в величину погрешности.
2) Исходную задачу рассмотрим в следующей постановке
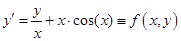 , ,  , , 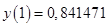 , ,  . .
По методу Эйлера с уточнением приближенное решение ищется по схеме
  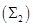
По данной схеме составим таблицу значений

| 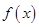
| 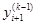
| 
| 
| 
| 
| |
| 1,38177
| 0,84147
|
|
| 0,84147
|
| | 1,05
| 1,38177
| 0,91056
| 1,38965
| 1,38571
| 0,91076
| Еще
| |
|
|
| 1,38984
| 1,38581
| 0,91076
| Все
| | 1,1
| 1,38984
| 0,98025
| 0,49896
| 0,94440
| 0,95798
| Еще
| |
|
|
| 1,36985
| 1,37984
| 0,97975
| Еще
| |
|
|
| 1,38964
| 1,38974
| 0,98025
| Еще
| |
|
|
| 1,39009
| 1,38997
| 0,98026
| Все
| | 1,15
| 1,39010
| 1,04976
| 1,38260
| 1,38635
| 1,04958
| Еще
| |
|
|
| 1,38244
| 1,38627
| 1,04957
| Все
| | 1,2
| 1,38243
| 1,11869
| 1,36707
| 1,37475
| 1,11831
| Еще
| |
|
|
| 1,30947
| 1,34595
| 1,11687
| Еще
| |
|
|
| 1,36555
| 1,37399
| 1,11827
| Еще
| |
|
|
| 1,36672
| 1,37458
| 1,11830
| Все
| | 1,25
| 1,36675
| 1,18661
| 1,34344
| 1,35509
| 1,18603
| Еще
| |
|
|
| 1,34297
| 1,35486
| 1,18602
| Все
|

| 
| 
| 
| 
| 
| |
| 0,84147
|
| 0,84147
| 0,00000
| 0,00000
| | 1,05
| 0,91076
| Еще
|
|
|
| |
| 0,91076
| Все
| 0,91079
| 0,00013
| 0,00004
| | 1,1
| 0,95798
| Еще
|
|
|
| |
| 0,97975
| Еще
|
|
|
| |
| 0,98025
| Еще
|
|
|
| |
| 0,98026
| Все
| 0,98033
| 0,00025
| 0,00007
| | 1,15
| 1,04958
| Еще
|
|
|
| |
| 1,04957
| Все
| 1,04968
| 0,00038
| 0,00011
| | 1,2
| 1,11831
| Еще
|
|
|
| |
| 1,11687
| Еще
|
|
|
| |
| 1,11827
| Еще
|
|
|
| |
| 1,11830
| Все
| 1,11845
| 0,00050
| 0,00015
| | 1,25
| 1,18603
| Еще
|
|
|
| |
| 1,18602
| Все
| 1,18623
| 0,00063
| 0,00022
|
Где признак окончания итерации  обозначен символом обозначен символом  . .
Построим графики точных и приближенных значений функции  , а так же графики абсолютных погрешностей (где , а так же графики абсолютных погрешностей (где  соответствует погрешности соответствует погрешности  , а , а 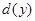 - погрешности - погрешности  ). ).
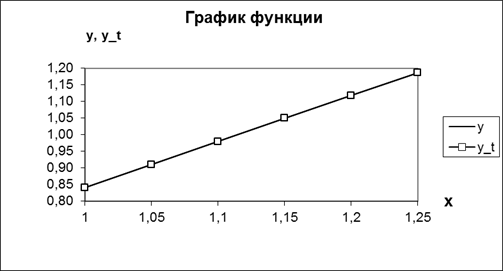
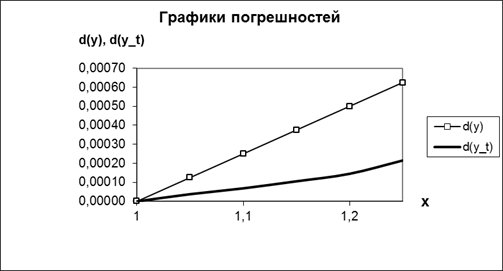
Вывод. Из полученных приближенных значений и графиков следует, что метод Эйлера с уточнением позволяет хорошо описать искомую функцию как на качественном, так и количественном уровне, хотя и дает завышенную погрешность по сравнению с точным решением (графики  и и 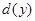 ). Поэтому метод Эйлера с уточнением может быть использован для практического применения нахождения приближенного решения искомой функции. ). Поэтому метод Эйлера с уточнением может быть использован для практического применения нахождения приближенного решения искомой функции.
Лабораторная работа 15. Методы обработки экспериментальных данных
Цель работы: 1. Изучить основы метода наименьших квадратов.
2. Научиться решать задачу аппроксимации дискретной зависимости  непрерывной функцией непрерывной функцией  определенного класса. определенного класса.
3. Освоить методику применения программных продуктов MSExcel для построения линейной и полиномиальной зависимостей по заданным эмпирическим данным.
Задание: Методом наименьших квадратов по заданным эмпирическим данным построить
1. линейную регрессию  . .
2. квадратичную регрессию  . .
2. Индивидуальные задания
| Вариант
| З а д а н и е
| |
| В таблице приведены данные численности занятого населения (х,млн.) и валового выпуска продукции (у, у.е.).
В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Спрогнозировать валовой выпуск продукции в случае, если занятое население увеличится на 10% по сравнению с последними данными (90 млн.) методом наименьших квадратов. Спрогнозировать валовой выпуск продукции в случае, если занятое население увеличится на 10% по сравнению с последними данными (90 млн.)
| |
| В таблице приведены данные об уровне безработицы (х) и уровне преступности (у) в некотором населенном пункте.
| хi
| 0,5
| 1,2
|
| 3,1
|
| 5,2
| 5,9
| 6,1
| 6,2
| 6,3
| | уi
| 4,25
| 4,32
| 4,4
| 4,51
| 4,6
| 4,72
| 4,79
| 4,9
| 5,0
| 5,2
| В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Спрогнозировать уровень преступности в случае, когда безработица отсутствует. методом наименьших квадратов. Спрогнозировать уровень преступности в случае, когда безработица отсутствует.
| |
| В таблице приведены данные о динамике темпов прироста курса акций (y, в %) за определенный период (t – одна неделя).
| ti
|
|
|
|
|
|
|
|
|
|
| | уi
| 10,2
| 8,3
| 5,4
| 4,1
| 2,2
|
| -1,6
| -3,9
| -5,9
| -7,8
| В предположении, что между t и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Сделать выводы о возможной динамике темпов прироста на 12 неделе. методом наименьших квадратов. Сделать выводы о возможной динамике темпов прироста на 12 неделе.
| |
| Торговое предприятие имеет сеть, состоящую из 10 магазинов, информация о деятельности которых: годовой товарооборот (у, млн. руб.) и торговая площадь (х, тыс. м2) представлена в таблице.
| хi
| 0,24
| 0,41
| 0,55
| 0,58
| 0,78
| 0,94
| 0,98
| 1,21
| 1,28
| 1,32
| | у i
| 19,8
| 38,1
| 41,0
| 43,1
| 56,3
| 68,5
| 75,0
| 89,1
| 91,1
| 91,3
| В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Спрогнозировать годовой товарооборот в случае, если торговая площадь составит ровно 1 тыс. м2. методом наименьших квадратов. Спрогнозировать годовой товарооборот в случае, если торговая площадь составит ровно 1 тыс. м2.
| |
| Показатели по объему производства (х, у.е.) и затратам (у, тыс. руб.), взятые из отчетной ведомости предприятия за 10 месяцев, приведены в таблице.
| хi
| 2,32
| 2,33
| 2,38
| 2,41
| 2,44
| 2,48
| 2,51
| 2,55
| 2,58
| 2,60
| | у i
|
|
|
|
|
|
|
|
|
|
| Полагая, что зависимость между х и у задается формулой  , где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b методом наименьших квадратов. Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е. , где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b методом наименьших квадратов. Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е.
| |
| В таблице приведена динамика валового выпуска (у, у.е.) за последние 10 лет (x – год)
Предполагая линейную зависимость валового выпуска от времени, определить параметры линейной регрессии  , используя метод наименьших квадратов. Получить прогноз валового выпуска на следующий год. , используя метод наименьших квадратов. Получить прогноз валового выпуска на следующий год.
| |
| Показатели стоимости основных производственных фондов (х, млн. руб.) и среднесуточной производительности (у, тонны) приведены в таблице.
| хi
| 2,1
| 2,3
| 2,4
| 2,9
| 4,1
| 4,7
| 5,5
| 7,2
| 10,2
| 14,3
| | у i
|
|
|
|
|
|
|
|
|
|
| Предполагая линейную зависимость у от х, определить параметры линейной регрессии  , используя метод наименьших квадратов. Получить прогноз среднесуточной производительности при стоимости основных производственных фондов 16 млн. руб. , используя метод наименьших квадратов. Получить прогноз среднесуточной производительности при стоимости основных производственных фондов 16 млн. руб.
| |
| В таблице приведены данные о количестве пропусков занятий (х) студентом в течение учебного семестра и результатах (у, %) написания экзаменационного теста.
Предполагая наличие линейной зависимости между х и у определить параметры линейной регрессии  , используя метод наименьших квадратов. Получить прогноз результатов теста при отсутствии пропусков. , используя метод наименьших квадратов. Получить прогноз результатов теста при отсутствии пропусков.
| |
| В таблице приведены данные об объемах производства (x, у.е.) некоторой компании в течение 10 месяцев и соответствующей операционной прибылью (y,тыс. руб.).
В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Сделать выводы о возможной месячной прибыли, если объем производства достигнет 600 у.е. методом наименьших квадратов. Сделать выводы о возможной месячной прибыли, если объем производства достигнет 600 у.е.
| |
| В таблице приведены данные об уровне безработицы (х) и уровне преступности (у) в некотором населенном пункте.
| хi
| 0,6
| 1,3
| 2,2
| 3,3
| 4,2
| 5,3
| 6,0
| 6,3
| 6,4
| 6,5
| | уi
| 4,2
| 4,27
| 4,32
| 4,47
| 4,53
| 4,68
| 4,85
| 5,01
| 5,15
| 5,22
| В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Спрогнозировать уровень преступности в случае, когда безработица отсутствует. методом наименьших квадратов. Спрогнозировать уровень преступности в случае, когда безработица отсутствует.
| |
| В таблице приведены данные численности занятого населения (х,млн.) и валового выпуска продукции (у,у.е.).
В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Спрогнозировать валовой выпуск продукции в случае, если занятое население увеличится на 10% по сравнению с начальными данными (80 млн.) методом наименьших квадратов. Спрогнозировать валовой выпуск продукции в случае, если занятое население увеличится на 10% по сравнению с начальными данными (80 млн.)
| |
| Показатели по объему производства (х, у.е.) и затратам (у, тыс. руб.), взятые из отчетной ведомости предприятия за 10 месяцев, приведены в таблице.
| хi
| 4,25
| 4,3
| 4,4
| 4,42
| 4,45
| 4,5
| 4,53
| 4,55
| 4,6
| 4,62
| | у i
|
|
|
|
|
|
|
|
|
|
| Полагая, что зависимость между х и у задается формулой  , где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b методом наименьших квадратов. Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е. , где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b методом наименьших квадратов. Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е.
| |
| В таблице приведена сведения об объеме спроса (у, у.е.) на некоторую продукцию и цены на эту продукцию (х, тыс. руб.).
| хi
|
| 10,6
|
|
| 12,5
| 12,8
|
| 13,2
| 13,3
| 13,7
| | у i
|
|
|
|
|
|
|
|
|
|
| Предполагая линейную зависимость объема спроса от цены на продукцию, определить параметры линейной регрессии  , используя метод наименьших квадратов. Получить прогноз объема спроса в случае, если цена на продукцию достигнет 14 тыс. руб. , используя метод наименьших квадратов. Получить прогноз объема спроса в случае, если цена на продукцию достигнет 14 тыс. руб.
| |
| Показатели стоимости основных производственных фондов (х, млн. руб.) и среднесуточной производительности (у, тонны) приведены в таблице.
| хi
| 2,6
| 2,8
| 2,9
| 3,4
| 4,6
| 5,2
| 6,1
| 7,7
| 10,6
| 14,0
| | у i
|
|
|
|
|
|
|
|
|
|
| Предполагая линейную зависимость у от х, определить параметры линейной регрессии  , используя метод наименьших квадратов. Получить прогноз среднесуточной производительности при стоимости основных производственных фондов 2 млн. руб. , используя метод наименьших квадратов. Получить прогноз среднесуточной производительности при стоимости основных производственных фондов 2 млн. руб.
| |
| Торговое предприятие имеет сеть, состоящую из 10 магазинов, информация о деятельности которых: годовой товарооборот (у, млн. руб.) и торговая площадь (х, тыс. м2) представлена в таблице.
| хi
| 0,25
| 0,42
| 0,57
| 0,59
| 0,79
| 0,95
| 0,99
| 1,23
| 1,29
| 1,33
| | у i
| 21,9
| 40,1
| 43,2
| 44,3
| 58,3
| 70,6
| 77,2
| 91,2
| 93,2
| 93,4
| В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии  методом наименьших квадратов. Спрогнозировать годовой товарооборот в случае, если торговая площадь составит ровно 1 тыс. м2. методом наименьших квадратов. Спрогнозировать годовой товарооборот в случае, если торговая площадь составит ровно 1 тыс. м2.
|
Основная литература:
1. Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков Численные методы, М. Лаборатория базовых знаний, 2010. – 632 с.
2. В.И.Киреев, А.В.Пантелеев «Численные методы в примерах и задачах». М.: «Высшая школа», 2008. -480 с.
3. В.М. Заварыкин, В.Г. Житомирский, М.П.Лапчик. Численные методы.- М.: Просвещение, 1990. –176 с.
4. Байғожанова Д.С., Ермекова Н.С. Сандық әдістер:оқу құралы. Талдықорған: 2011 ж. –200 б.
5. Шакенов Қ.Қ. Есептеу математикасы әдістері. Оқу құралы. «PrintS» баспасы, Алматы, 2009 ж., –193 б.
6. В.М.Вержбицкий. Линейная алгебра и нелинейные уравнения М.Высшая школа, 2000, - 266с.
7. Алексеев Е.Р. Mathcad 12 / Е.Р. Алексеев, О.В. Чеснокова.- М.: НТ Пресс, 2005.-345.
8. Математический анализ и обыкновенные дифференциальные уравнения. М. Высшая школа, 2001.-382с.
Дополнительная работа
9. Искаков К.Т. Численные методы. Учебные пособие. Караганда: Болашақ-Баспа, 2004.-297 с.
10. Лапчик М.П., М.И.Рагулина, Е.Л.Хеннер «Численные методы», М.Издательский центр «Академия», 2004, -384с.
11. Султангазин О.М., Атамбаев С.А. Есептеу әдістерінің қысқаша теориясы 1-кітап.Оқу құралы, Алматы, «Білім,»1995, -272 -б
12. Атанбаев С.А. Алгебраның есептеу әдістері / Оқу қуралы. /.Алматы, Республика баспа кабинеті, 1994-115 -б.
13. Бидайбеков Е.Ы., Корнилов В.С. Математическое моделирование и численные методы. Введение-Алматы,1998.-80с.
14. Джон, Г.Мэтьюз, Куртис, Д.Финк «Численные методы»использования 3-издания:Пер.с англ. М. Издательский дом «Вильямс», 2001-720с.
15. А.И.Плисс, Н.А.Сливина «Лабораторный практикум по вычислительной математике», М, 1994.
16. Н.С.Бахвалов, А.В.Лапин, Е.В.Чижонков Численные методы в задачах и упражнениях. М. Высшая школа, 2000.
17. Практикум на ПВЭМ ч.1.Численные методы алгебры. Методическая разработка./сост. Е.Ы.Бидайбеков, М.А.Бектемесов, В.С.Корнилов /.Алматы:АГУ им. Абая, 1995-47с.
18. А.И.Плисс, Н.А.Сливина Math Cad 2000. Математический практикум. М.Финансы и статистика, 2010. -655с.
19. Н.С.Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. М., Наука, 2010 г.
20. Информатика мен ЕТ негіздері. Орта оқу орындарына арналған байқау оқу құралы.- Алматы: Мектеп, 2004.- 96бет.
21. Бобровский С.И. Delphi 7: Учебный курс / С.И. Бобровский.- СПб.: Питер, 2005.- 736с.
22. Ахметов Қ.А. Менеджментте матем-лық әдістер: Оқулық. /-Алматы: Эверо, 2005.- 516 бет.
23. Введение в матем.ое моделирование: Учеб. пособие / Под ред. П.В.Турусова.-М.: Логос, 2008.- 440 с.
|



 :
: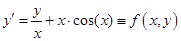 ,
, 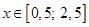 ,
,  .
. ,
,  .
. 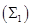
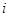









 ,
,  . Используя исходное уравнение,
. Используя исходное уравнение, .
. ,
, 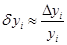
 .
. ,
,  ,
, соответствует погрешности
соответствует погрешности  - погрешности
- погрешности 

 в величину погрешности.
в величину погрешности. ,
, 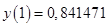 ,
,  .
.

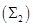

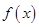
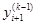





 обозначен символом
обозначен символом 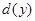 - погрешности
- погрешности 

 непрерывной функцией
непрерывной функцией  определенного класса.
определенного класса. .
. .
. методом наименьших квадратов. Спрогнозировать валовой выпуск продукции в случае, если занятое население увеличится на 10% по сравнению с последними данными (90 млн.)
методом наименьших квадратов. Спрогнозировать валовой выпуск продукции в случае, если занятое население увеличится на 10% по сравнению с последними данными (90 млн.) методом наименьших квадратов. Сделать выводы о возможной динамике темпов прироста на 12 неделе.
методом наименьших квадратов. Сделать выводы о возможной динамике темпов прироста на 12 неделе. , где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b методом наименьших квадратов. Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е.
, где b – постоянные затраты в тыс. руб., k – переменные затраты на 1 условную единицу продукции, определить параметры k и b методом наименьших квадратов. Рассчитать возможные затраты на производство в случае, если объем производства достигнет 3 у.е.


