

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Образец выполнения лабораторной работы № 8
(Интерполирование функций. Полином Лагранжа)
Постановка задачи. Дана функция  своими значениями своими значениями 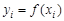 , где , где  , , 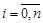 . Найти интерполирующую функцию определенного класса . Найти интерполирующую функцию определенного класса  , такую что , такую что  , для , для  . .
Задача интерполяции заключается в нахождении значения функции  при при   , для чего полагают, что , для чего полагают, что 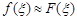 . .
А) Рассмотрим решение задачи интерполяции для функции заданной таблично, используя метод Лагранжа для не равноотстоящих узлов.

| 0,200000
| 0,306000
| 0,468180
| 0,716315
| 1,095963
| 1,676823
| 2,565539
| 
| 1,020067
| 1,047184
| 1,111613
| 1,267713
| 1,663140
| 2,767751
| 6,542271
|
Найти  , при , при  . .

| 0,200000
| 0,306000
| 0,468180
| 0,716315
| 1,095963
| 1,676823
| 2,565539
| 
| 1,020067
| 1,047184
| 1,111613
| 1,267713
| 1,663140
| 2,767751
| 6,542271
|

| 2,10
| Замечание. В дальнейшем промежуточные значения будут представлены в тексте с четырьмя знаками после запятой, хотя все вычисления будут проводиться с шестью знаками после запятой.

| 1,9000
| 1,7940
| 1,6318
| 1,3837
| 1,0040
| 0,4232
| -0,4655
| Таблица разностей 
|
| 0,2000
| 0,3060
| 0,4682
| 0,7163
| 1,0960
| 1,6768
| 2,5655
| | 0,2000
|
| 0,1060
| 0,2682
| 0,5163
| 0,8960
| 1,4768
| 2,3655
| | 0,3060
| -0,1060
|
| 0,1622
| 0,4103
| 0,7900
| 1,3708
| 2,2595
| | 0,4682
| -0,2682
| -0,1622
|
| 0,2481
| 0,6278
| 1,2086
| 2,0974
| | 0,7163
| -0,5163
| -0,4103
| -0,2481
|
| 0,3796
| 0,9605
| 1,8492
| | 1,0960
| -0,8960
| -0,7900
| -0,6278
| -0,3796
|
| 0,5809
| 1,4696
| | 1,6768
| -1,4768
| -1,3708
| -1,2086
| -0,9605
| -0,5809
|
| 0,8887
| | 2,5655
| -2,3655
| -2,2595
| -2,0974
| -1,8492
| -1,4696
| -0,8887
|
|
Таблица значений
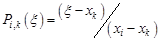
| 
| 
| |
| -16,9245
| -6,0848
| -2,6799
| -1,1206
| -0,2865
| 0,1968
| -17,4407090
| -17,7906917
| | -17,9245
|
| -10,0618
| -3,3723
| -1,2710
| -0,3087
| 0,2060
| 49,1657194
| 51,4855547
| | -7,0848
| 11,0618
|
| -5,5763
| -1,5993
| -0,3501
| 0,2220
| -54,3186589
| -60,3813274
| | -3,6799
| 4,3723
| 6,5763
|
| -2,6447
| -0,4406
| 0,2517
| 31,0373295
| 39,3464261
| | -2,1206
| 2,2710
| 2,5993
| 3,6447
|
| -0,7285
| 0,3168
| -10,5296185
| -17,5122296
| | -1,2865
| 1,3087
| 1,3501
| 1,4406
| 1,7285
|
| 0,5238
| 2,9651590
| 8,2068217
| | -0,8032
| 0,7940
| 0,7780
| 0,7483
| 0,6832
| 0,4762
|
| 0,1207786
| 0,7901663
| |
|
|
|
|
|
| 
| 4,1447200
|
Графическая интерпретация исходных значений и результата дают следующую картину, где точкой показан получаемый результат  . Из данного рисунка можно сказать, что полученное приближенное решение задачи интерполяции вполне отвечает исходным данным. . Из данного рисунка можно сказать, что полученное приближенное решение задачи интерполяции вполне отвечает исходным данным.
Оценка погрешности приближения  . .
Оценим погрешность приближения с помощью выражения  , ,  . Одним из возможных способов оценки погрешности является способ сведения задачи интерполяции в не равноотстоящих точках к задаче на равноотстоящих точках, что позволит оценить . Одним из возможных способов оценки погрешности является способ сведения задачи интерполяции в не равноотстоящих точках к задаче на равноотстоящих точках, что позволит оценить  с помощью выражения с помощью выражения  . Для этого необходимо найти конечные разности в равноотстоящих узлах . Для этого необходимо найти конечные разности в равноотстоящих узлах  , , 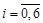 , , 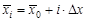 , , 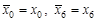  . С помощью интерполирующего многочлена Лагранжа найдем . С помощью интерполирующего многочлена Лагранжа найдем  , , 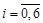 , затем составим конечные разности: , затем составим конечные разности: 

| 0,2000
| 0,5943
| 0,9885
| 1,3828
| 1,7770
| 2,1713
| 2,5655
| 
| 1,0201
| 1,1819
| 1,5297
| 2,1184
| 3,0407
| 4,4423
| 6,5423
|

| 
| 
| 
| 
| 
| 
| | 1,0201
| 0,1618
| 0,1860
| 0,0549
| 0,0378
| 0,0152
| 0,0052
| | 1,1819
| 0,3478
| 0,2409
| 0,0927
| 0,0530
| 0,0204
|
| | 1,5297
| 0,5887
| 0,3336
| 0,1457
| 0,0734
|
|
| | 2,1184
| 0,9223
| 0,4793
| 0,2191
|
|
|
| | 3,0407
| 1,4016
| 0,6984
|
|
|
|
| | 4,4423
| 2,1000
|
|
|
|
|
| | 6,5423
|
|
|
|
|
|
|
Если обозначить через  , где , где 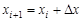 , то , то  . .

| 
| 
| 
| 
| 
|
| | -1,1808
| -0,1808
| 0,8192
| 1,8192
| 2,8192
| 3,8192
|
| | |
|
|
|
| 
| 0,00002474
|
Получим решение:  , ,  0,00002474. 0,00002474.
Определим число верных знаков. Так как  0,00005, то при 0,00005, то при  имеем имеем  . После округления получим . После округления получим  , , 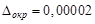 , ,  . Так как . Так как  , то , то  . Следовательно, в полученном результате все знаки верные. . Следовательно, в полученном результате все знаки верные.
Ответ:  . .
Лабораторная работа 9.: Интерполирование функции. Полиномы Ньютона.
Задание:
1) Найти приближенное значение функции при заданном значении аргумента  с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах; с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах;


2) Оценить погрешность полученного значения.
|
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
|
| 0,9950
| 0,9988
| 0,9512
| 0,3679
| 0,3679
| 0,4311
| 0,6664
| 1,7151
| 1,0806
| 6,8621
| |
| 1,15
| 1,1424
| 1,1481
| 1,0857
| 0,3064
| 0,2317
| 0,3044
| 0,4329
| 1,7834
| 1,0805
| 7,4816
| |
| 1,3
| 1,2890
| 1,2973
| 1,2182
| 0,2399
| 0,1419
| 0,2198
| 0,2406
| 1,8803
| 0,9042
| 8,0055
| |
| 1,45
| 1,4348
| 1,4462
| 1,3486
| 0,1771
| 0,0842
| 0,1635
| 0,0903
| 1,9696
| 0,5067
| 8,4128
| 
| 1,6
| 1,5796
| 1,5949
| 1,4770
| 0,1237
| 0,0483
| 0,1263
| -0,0178
| 1,9978
| -0,1495
| 8,6805
| |
| 1,75
| 1,7233
| 1,7433
| 1,6034
| 0,0819
| 0,0267
| 0,1021
| -0,0861
| 1,9035
| -1,0918
| 8,7858
| |
| 1,9
| 1,8658
| 1,8914
| 1,7278
| 0,0514
| 0,0142
| 0,0872
| -0,1185
| 1,6344
| -2,3342
| 8,7075
| 
| =
| 1,23
| 1,47
| 1,52
| 1,16
| 1,23
| 1,47
| 1,52
| 1,48
| 1,18
| 1,25
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
|
| 0,2955
| 0,8408
| 0,6694
| 0,7358
| 1,0000
| 1,1651
| 0,6670
| 1,7552
| 1,6829
| 2,9736
| |
| 1,13
| 0,3758
| 0,9499
| 0,5508
| 0,4936
| 1,0250
| 1,0929
| 0,4623
| 1,9088
| 2,3097
| 3,2084
| |
| 1,26
| 0,4650
| 1,0589
| 0,4532
| 0,3245
| 1,1013
| 1,0797
| 0,2885
| 2,0362
| 3,0231
| 3,4131
| 
| 1,39
| 0,5630
| 1,1678
| 0,3729
| 0,2084
| 1,2371
| 1,1206
| 0,1459
| 2,1352
| 3,8012
| 3,5816
| |
| 1,52
| 0,6694
| 1,2767
| 0,3069
| 0,1306
| 1,4502
| 1,2181
| 0,0352
| 2,2035
| 4,6148
| 3,7078
| |
| 1,65
| 0,7838
| 1,3854
| 0,2525
| 0,0797
| 1,7713
| 1,3812
| -0,0443
| 2,2392
| 5,4279
| 3,7850
| |
| 1,78
| 0,9060
| 1,4940
| 0,2078
| 0,0473
| 2,2520
| 1,6261
| -0,0948
| 2,2407
| 6,1986
| 3,8070
| 
| =
| 1,23
| 1,47
| 1,35
| 1,16
| 1,20
| 1,47
| 1,60
| 1,48
| 1,18
| 1,25
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
|
| 0,8896
| 0,5414
| 0,7955
| 1,5576
| 1,1884
| 1,2693
| 0,1034
| 0,9483
| 1,6829
| 1,9093
| |
| 1,08
| 1,0936
| 0,5849
| 0,6732
| 1,3835
| 1,2362
| 1,2220
| 0,6080
| 0,8732
| 2,2220
| 1,6681
| |
| 1,16
| 1,3230
| 0,6284
| 0,5743
| 1,2316
| 1,3132
| 1,1956
| 1,0359
| 0,7750
| 2,8621
| 1,4193
| 
| 1,24
| 1,5786
| 0,6720
| 0,4938
| 1,0982
| 1,4238
| 1,1863
| 1,3901
| 0,6556
| 3,6065
| 1,1620
| |
| 1,32
| 1,8609
| 0,7156
| 0,4276
| 0,9801
| 1,5749
| 1,1914
| 1,6745
| 0,5176
| 4,4560
| 0,8956
| |
| 1,4
| 2,1705
| 0,7593
| 0,3728
| 0,8752
| 1,7765
| 1,2083
| 1,8936
| 0,3640
| 5,4082
| 0,6197
| |
| 1,48
| 2,5077
| 0,8031
| 0,3272
| 0,7815
| 2,0432
| 1,2347
| 2,0529
| 0,1982
| 6,4569
| 0,3345
| 
| =
| 1,23
| 1,47
| 1,15
| 1,16
| 1,25
| 1,47
| 1,10
| 1,14
| 1,05
| 1,25
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 1,5
| 1,4832
| 1,4958
| 1,3916
| 0,1581
| 0,0703
| 0,1493
| 0,0497
| 1,9888
| 0,3183
| 8,5186
| |
| 1,61
| 1,5892
| 1,6048
| 1,4855
| 0,1205
| 0,0465
| 0,1243
| -0,0236
| 1,9960
| -0,2032
| 8,6928
| |
| 1,72
| 1,6946
| 1,7136
| 1,5783
| 0,0893
| 0,0302
| 0,1061
| -0,0754
| 1,9350
| -0,8795
| 8,7788
| 
| 1,83
| 1,7994
| 1,8223
| 1,6700
| 0,0643
| 0,0192
| 0,0932
| -0,1075
| 1,7840
| -1,7167
| 8,7681
| |
| 1,94
| 1,9036
| 1,9309
| 1,7607
| 0,0450
| 0,0120
| 0,0844
| -0,1218
| 1,5296
| -2,7164
| 8,6532
| |
| 2,05
| 2,0071
| 2,0392
| 1,8503
| 0,0307
| 0,0073
| 0,0791
| -0,1199
| 1,1712
| -3,8753
| 8,4272
| |
| 2,16
| 2,1098
| 2,1474
| 1,9389
| 0,0203
| 0,0044
| 0,0769
| -0,1033
| 0,7241
| -5,1853
| 8,0850
| 
| =
| 1,55
| 1,65
| 1,85
| 1,65
| 1,90
| 2,10
| 1,80
| 1,55
| 1,88
| 2,10
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
|
| 1,1293
| 1,6775
| 0,1494
| 9,1578
| 3,6945
| 2,29858
| -0,1223
| 2,1612
| 7,2744
| 3,7024
| |
| 2,14
| 1,2814
| 1,7941
| 0,1211
| 4,7939
| 5,3591
| 2,96157
| -0,1070
| 2,0549
| 7,7151
| 3,5343
| |
| 2,28
| 1,4407
| 1,9105
| 0,0981
| 2,4234
| 8,1191
| 3,87202
| -0,0693
| 1,9042
| 7,8899
| 3,2825
| 
| 2,42
| 1,6066
| 2,0268
| 0,0796
| 1,1825
| 12,8401
| 5,08455
| -0,0112
| 1,7086
| 7,7373
| 2,9456
| |
| 2,56
| 1,7784
| 2,1428
| 0,0645
| 0,5566
| 21,1913
| 6,63426
| 0,0643
| 1,4680
| 7,2005
| 2,5245
| |
| 2,7
| 1,9556
| 2,2586
| 0,0523
| 0,2527
| 36,4794
| 8,50701
| 0,1502
| 1,1826
| 6,2312
| 2,0228
| |
| 2,84
| 2,1374
| 2,3742
| 0,0424
| 0,1106
| 65,4834
| 10,6032
| 0,2343
| 0,8533
| 4,7916
| 1,4468
| 
| =
| 2,10
| 2,20
| 2,75
| 2,50
| 2,20
| 2,47
| 2,30
| 2,60
| 2,25
| 2,80
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| Вариант
|
|
|
|
|
|
|
|
|
|
| |
| 0,5
| 0,4994
| 0,4998
| 0,4877
| 0,3894
| 1,5576
| 1,5737
| 1,9428
| 1,8105
| 0,4388
| 4,2860
| |
| 1,01
| 1,0049
| 1,0087
| 0,9603
| 0,3642
| 0,3570
| 0,4210
| 0,6495
| 1,7183
| 1,0851
| 6,9060
| |
| 1,52
| 1,5025
| 1,5156
| 1,4088
| 0,1508
| 0,0653
| 0,1442
| 0,0347
| 1,9941
| 0,2346
| 8,5564
| 
| 2,03
| 1,9883
| 2,0196
| 1,8341
| 0,0330
| 0,0080
| 0,0798
| -0,1214
| 1,2436
| -3,6531
| 8,4768
| |
| 2,54
| 2,4585
| 2,5195
| 2,2371
| 0,0040
| 0,0006
| 0,0935
| 0,0523
| -0,9994
| -10,6379
| 5,9763
| |
| 3,05
| 2,9092
| 3,0146
| 2,6186
| 0,0003
| 0,0000
| 0,2481
| 0,3152
| -1,9891
| -18,5270
| 1,0712
| |
| 3,56
| 3,3368
| 3,5038
| 2,9795
| 0,0000
| 0,0000
| 1,1933
| 0,0348
| -1,9876
| -23,1607
| -5,1966
| 
| =
| 0,72
| 1,40
| 1,70
| 1,30
| 0,70
| 2,00
| 2,50
| 2,48
| 1,20
| 3,1
| | | | | | | | | | | | | | |
|



 своими значениями
своими значениями 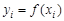 , где
, где  ,
, 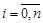 . Найти интерполирующую функцию определенного класса
. Найти интерполирующую функцию определенного класса  , такую что
, такую что  , для
, для  .
.
 , для чего полагают, что
, для чего полагают, что 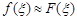 .
.

 , при
, при  .
.


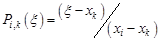



 . Из данного рисунка можно сказать, что полученное приближенное решение задачи интерполяции вполне отвечает исходным данным.
. Из данного рисунка можно сказать, что полученное приближенное решение задачи интерполяции вполне отвечает исходным данным.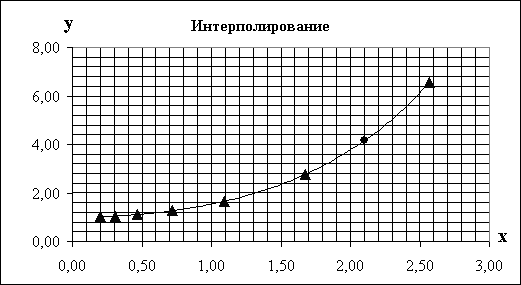
 .
. ,
,  . Одним из возможных способов оценки погрешности является способ сведения задачи интерполяции в не равноотстоящих точках к задаче на равноотстоящих точках, что позволит оценить
. Одним из возможных способов оценки погрешности является способ сведения задачи интерполяции в не равноотстоящих точках к задаче на равноотстоящих точках, что позволит оценить  с помощью выражения
с помощью выражения  . Для этого необходимо найти конечные разности в равноотстоящих узлах
. Для этого необходимо найти конечные разности в равноотстоящих узлах  ,
, 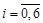 ,
, 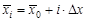 ,
, 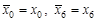
 . С помощью интерполирующего многочлена Лагранжа найдем
. С помощью интерполирующего многочлена Лагранжа найдем  ,
, 







 , где
, где 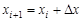 , то
, то  .
.






 ,
,  0,00005, то при
0,00005, то при  имеем
имеем  . После округления получим
. После округления получим  ,
, 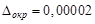 ,
,  . Так как
. Так как  , то
, то  . Следовательно, в полученном результате все знаки верные.
. Следовательно, в полученном результате все знаки верные. .
.






