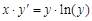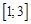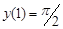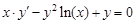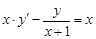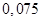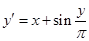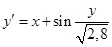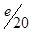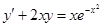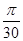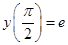Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образец выполнения лабораторной работы №10-11Содержание книги
Поиск на нашем сайте
(Численное интегрирование) Задание: Дан интеграл 1) Найти приближенное значение интеграла 2) Найти приближенное значение интеграла 3) Найти приближенное значение интеграла 4) Найти приближенное значение интеграла 5) Сравнить полученные результаты. Отрезок
1) Вычислим значение интеграла и его погрешность методом левых прямоугольников используя выражения
Тогда получим Так как
Таким образом оставшиеся цифры в записи числа верные. Ответ: Вычислим значение интеграла и его погрешность методом правых прямоугольников
Тогда получим Так как
Таким образом оставшиеся цифры в записи числа верные.
Ответ: 2) Методом средних прямоугольников вычислим значение интеграла и его погрешность
Тогда имеем Таким образом оставшиеся цифры в записи числа верные. Ответ: 3) Используя формулу трапеции и соответствующую ей оценку погрешности
получим Так как
Таким образом оставшиеся цифры в записи числа верные. Ответ: 4) Используя формулу Симпсона и соответствующую ей оценку погрешности
получим Так как
Ответ: 5) Сравнение результатов. Лабораторная работа № 12-14 Тема: Приближенное решение обыкновенных дифференциальных уравнений первого порядка. Задача Коши. Задание: Найти приближенные значения решения 1) метод Эйлера; 2) усовершенствованный метод ломаных; 3) метод Эйлера-Коши; 4) метод Эйлера с уточнением; 5) метод Рунге-Кутта четвертого порядка. Для тестовых примеров найти относительные погрешности и сравнить полученные результаты. Построить графики точного и численного решений. Оценить погрешность приближенного решения заданного уравнения в выбранной точке, построить график численного решения. Вопросы самоконтроля. 1) Постановка задачи Коши для обыкновенных дифференциальных уравнений (ОДУ). Геометрическая иллюстрация. 2) Основные положения метода Эйлера. Геометрическая интерпретация. 3) Основные положения метода Эйлера-Коши. Геометрическая интерпретация. 4) Основные положения метода Эйлера с уточнением. Геометрическая интерпретация. 5) Метод Рунге-Кутта. Оценка погрешности метода на шаге. 6) Какой метод является более точным, какой менее точным?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.194.47 (0.011 с.) |

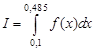 , где
, где 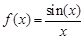 .
.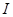 по формулам левых и правых прямоугольников с точностью
по формулам левых и правых прямоугольников с точностью  .
. по формуле Симпсона с точностью
по формуле Симпсона с точностью  разобьем на
разобьем на 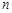 частей и найдем значения
частей и найдем значения 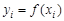 ,
, ,
,  ,
, 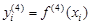 ,
,  ,
, 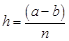 .
.





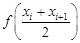
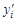



 ,
, 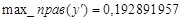 ,
,  ,
, 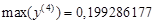 .
.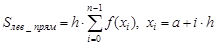 ,
,  .
. ;
;  .
. , то число верных знаков равно
, то число верных знаков равно  . Следовательно
. Следовательно  ,
, 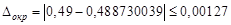 ,
, .
. .
. ,
,  .
. ;
;  .
. , то число верных знаков равно
, то число верных знаков равно  ,
, .
. .
. ,
,  .
.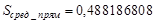 ;
;  . Так как
. Так как  , то число верных знаков равно
, то число верных знаков равно 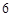 . Следовательно
. Следовательно  ,
,  ,
,  . Так как
. Так как 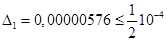 , то число верных знаков равно
, то число верных знаков равно  , тогда
, тогда 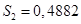 ,
, 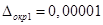 ,
,  . Очевидно, что
. Очевидно, что  .
.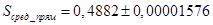 .
. ,
, 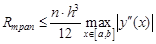
 ;
;  .
.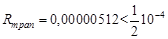 , то число верных знаков равно
, то число верных знаков равно  . Следовательно
. Следовательно  ,
,  ,
,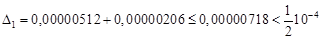 .
. .
. ,
, 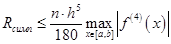
 ;
;  .
. , то число верных знаков равно
, то число верных знаков равно  . Следовательно
. Следовательно  ,
,  ,
,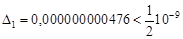 . Таким образом оставшиеся цифры в записи числа верные.
. Таким образом оставшиеся цифры в записи числа верные.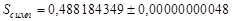 .
.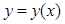 обыкновенного дифференциального уравнения (ОДУ)
обыкновенного дифференциального уравнения (ОДУ)  на отрезке
на отрезке 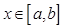 с шагом
с шагом 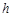 при начальном условии
при начальном условии  используя
используя