Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания по технике вычисленийСодержание книги
Поиск на нашем сайте
1. Все промежуточные вычисления следует заносить в бланк расчета. 2. Производя расчет, следует широко использовать возможности современных ЭВМ: запоминание постоянного множителя, накопление сумм и т.п. – чтобы избежать лишних записей (если вычисления на микрокалькуляторе). 3. В промежуточных вычислениях следует сохранить значащих цифр на две больше, чем дано в исходных данных. При записи ответа нужно оставить только один запасной знак. Пример 1. Методом Гаусса по схеме с выбором главного элемента в столбце решить систему
Решение представлено в бланке расчета. Таблица 1
1. Порядок заполнения таблицы
Прямой ход В первом столбце поставим номера разделов. Раздел первый
2. В графы, отведенные для матриц, записываем коэффициенты при неизвестных и свободные члены, приписывая в качестве двух запасных значащих цифр нули. 3. В каждой строке вычисляем алгебраическую сумму коэффициентов и свободного члена и записываем в столбец контрольных сумм. Так, например, для первой строки
4. Среди элементов первого столбца выбираем наибольший по абсолютной величине, подчеркиваем строку, в которой он стоит и выписываем ее в качестве первой строки в таблицу для обратного хода. Здесь главной будет первая строка, главный элемент равен 2,000. 5. Элементы всех строк первого столбца, кроме главного, делим на него и результат с противоположным знаком записываем в столбец
Раздел второй 6. Исключаем элементы первого столбца, кроме главного. Для этого главную строку, умноженную на
7. Контроль: складываем полученные коэффициенты при неизвестных и свободный член 8. Аналогично вычисляем вторую и третью строки второго раздела
9. Проводим контроль, как в п. 7.
10. Среди коэффициентов при неизвестном Далее, делим на главный элемент все числа, стоящие с ним в одном столбце (0,300 и -0,300), результаты записываем с противоположным знаком в качестве
11. Третий раздел будет иметь две строки. Главный элемент выбираем среди коэффициентов при
Обратный ход 1. Последняя строка таблицы соответствует уравнению 2. Контроль: вместо свободного члена
3. Найденное значение
Контроль:
4. Найденные значения
5. Из первого уравнения получим Проверка. Значения неизвестных
Значения невязок малы, т.е. нулей до первой значащей цифры больше, чем было знаков после запятой в исходных данных, значит, вычисления проведены верно. Невязки запишем на свободное место в столбец первого раздела. Ответ: Решением данной системы будет вектор
1. Матричные функции Excel Для решения задач линейной алгебры используются матричные функции Excel из категории математические: МУМНОЖ(<матрица1>;<матрица2>) – возвращает произведение матриц. МОБР(<матрица>) – возвращает матрицу, обратную к данной. МОПРЕД(<матрица>) – вычисляет определитель исходной квадратной матрицы. Порядок обращения к матричным функциям: Ø выделить блок, где будет размещен результат матричной операции; Ø Ø убрать окно соответствующей функции (с помощью кнопки) или отбуксировать его в сторону от исходных данных; Ø выделить исходную матрицу (бегущая пунктирная линия); Ø одновременно нажать клавиши Shift+Ctrl+Enter. 1. Реализация метода Гаусса средствами приложения Excel Пример 1.1. Найти решение системы линейных алгебраических уравнений
используя алгоритм метода Гаусса.
Последовательность действий: Возьмем чистый лист Excel, назовем его Гаусс. Введем расширенную матрицу системы, как показано на рис.1.1 в ячейки А3:D5. Первый этап, приведение матрицы системы к треугольной. 1. Поделим элементы первой строки на а11 .Для этого в ячейку А7 введем формулу А7=А3/A$3$ (*смотри сноску) и скопируем ее вправо до конца строки. 2. Умножим элементы первой строки на (-а21) и прибавим ко 2-ой строке. Для этого введем формулу А8=А7(-А$4$)+А4 и скопируем ее вправо до конца строки. 3. Умножим элементы первой строки на (- а31 ) и прибавим к 3-ей строке. Для этого введем формулу А9=А7(-А$5$)+А5 и скопируем ее вправо до конца строки. Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-ый шаг рис.1.1). 4. Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-ой и3-ей строк (смотри 2-ой шаг рис.1.1).
Рис.1.1. На этом первый этап метода Гаусса, закончен, матрица системы приведена к треугольной. Второй этап. Здесь последовательно найдем неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы: G4=D13/C13 (для вычисления x 3); G3=D12-C12*G4 (для вычисления x2); G2=D11-C11*G4-B11*G3 (для вычисления x1).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.192.96 (0.01 с.) |



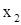
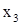
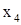


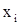

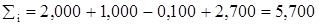 .
.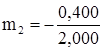 ,
, 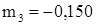 ,
, 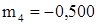 .
.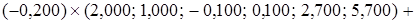
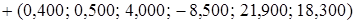 =
=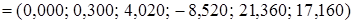 .
.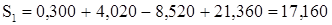 . Строчная сумма
. Строчная сумма 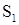 совпадает с контрольной
совпадает с контрольной 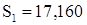 , значит, эта строка найдена без ошибки.
, значит, эта строка найдена без ошибки.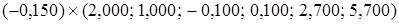 +
+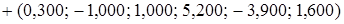 =
=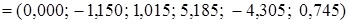 .
.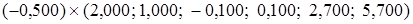 +
+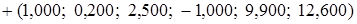 =
=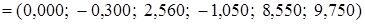 .
.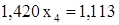 . Отсюда находим
. Отсюда находим 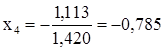 .
.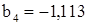 берем
берем 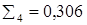 , находим
, находим 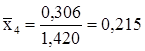 . Проверяем выполнение условия
. Проверяем выполнение условия 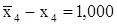 :
: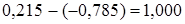 .
.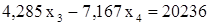 , отсюда
, отсюда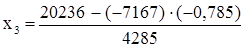 .
.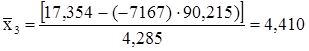 ,
,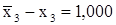 .
.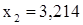 . Также по известным
. Также по известным 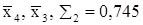 получим
получим 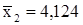 .
.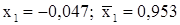 .
.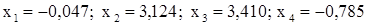 подставим в каждое из уравнений исходной системы и подсчитаем невязки (см. разд. 3):
подставим в каждое из уравнений исходной системы и подсчитаем невязки (см. разд. 3):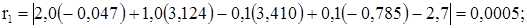
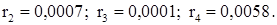
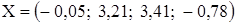 (в ответе оставляем только 1 запасную цифру).
(в ответе оставляем только 1 запасную цифру). в мастере функций выбрать нужную категорию и нужную функцию;
в мастере функций выбрать нужную категорию и нужную функцию;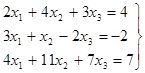 , (1.8)
, (1.8)