
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Эластичность спроса и предложенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. При цене 6 ед. спрос равен 2 ед., а предложение — 8 ед. Точка равновесия имеет координаты 4 ед. и 4 ед. Принимая линии спроса и предложения прямыми, с помощью графиков определить эластичность спроса и предложения для интервала цены от 4 до 5 единиц.
2. Известно, что при цене 1 доллар за фунт куриных окорочков дневной спрос составлял 800 фунтов, а после снижения цены до 0,8 доллара за фунт он составил 1000 фунтов. Чему равна точечная ценовая эластичность спроса на куриные окорочка? Чему равна дуговая эластичность спроса на куриные окорочка? Если цена вновь вырастет до 1 доллара за фунт, а дневной спрос упадет до 800 фунтов, сохранятся ли значения точечной и дуговой эластичности?
3. Кривая спроса D (рис. 3.1) проходит через точки А и В с координатами соответственно (8;3) и (2;6). Вычислить коэффициент эластичности спроса, если известно, что цена увеличивается.
4. Функция спроса задана формулой Qd = 12,5 — 1,5P, функция предложения Qs = 2 + 2Р а) Насколько необходимо увеличить цену, чтобы объем спроса уменьшился на 30%? б) Насколько необходимо увеличить цену, чтобы объем предложения увеличился на 40%?
5. Потребитель покупает два товара: х и у; в равновесии он направляет 70% своего дохода на приобретение товара х. Подсчитайте эластичность спроса по доходу товара у, зная, что для товара х она равна 1,5. 6. В таблице 4.1 представлены данные о структуре расходов семьи за два года (цены на товары А, Б, В, Г не меняются). Заполните таблицу 4.1.
Таблица 4.1.
7. Функция спроса на товар А равна: QDA = 4 PA - 5 PB, а функция предложения товара А равна: QSA = 3 + 2 РA+ 0,5 РB, где PA и РB — цены на товары А и В. Определить: а) при каких ценах на товары А и В равновесный объем товара А равен 30; б) как изменится равновесный объем товара А при росте цены товара В в 2 раза; в) значение перекрестной эластичности предложения товара А. Прокомментируйте результат.
8. Доход потребителя вырос с 2 до 4 тыс. руб. в год. Спрос на маргарин упал с 3 до 1 кг в год. Спрос на масло возрос с 6 до 8 кг в год. Определить эластичность спроса по доходу и характеру товара.
9. Цена на чай возросла с 10 до 20 руб. за кг. Спрос на сахар упал с 2 до 1 кг. Спрос на кофе возрос с 0,5 до 1,5 кг. Спрос на спички не изменился: 10 коробков. Определить перекрестную эластичность и тип товаров по цене чая. 10. Цена на некоторый товар возросла, ее относительное изменение, исчисленное по отношению к исходному значению, составило 0,25. Затем цена снизилась до прежнего уровня, причем теперь ее относительное изменение составило 0,2. Рассчитайте соответствующее относительное изменение цены по «методу средней точки».
11. Рынок некоторого товара, функционирующий в условиях налогообложения его производителей, характеризуется функцией спроса с единичной ценовой эластичностью и функцией предложения QS= - 20 + 2Р. Равновесный объем продаж при этом составлял 10 ед. товара. При отмене налога предложение товара возросло на 15 ед. для любого уровня цены. Сколько составит объем продаж данного товара после отмены на него налога.
12. Фирма имеет кривую спроса q = 200 - 0,5 Р. Зная, что цена равна 100, определить изменение дохода при увеличении количества проданной продукции на 1 ед. 13. Допустим, функция спроса линейна и задается как Qd = 180 – 3P. Какой будет ценовая эластичность спроса при цене 10 руб.? Тема 5. Потребительское поведение 1. Иванова Катя имеет в неделю 16 руб., которые она тратит на газеты и булочки. Каждая газета стоит 2 руб., а каждая булочка – 4 руб. В таблице 5.1. представлены функции совокупной полезности для Ивановой Кати от просмотра газет и поедания булочек.
Таблица 5.1.
Какую комбинацию газет и булочек должна выбрать Катя для оптимизации общей полезности?
2. Общая и предельная полезности товаров А, В, С представлены в таблице 5.2. Заполните пропуски. Таблица 5.2.
3. Студент ежемесячно получает 200 руб. на питание и развлечения. Цена условной единицы того и другого — 5 руб. Нарисовать бюджетную линию студента. Как изменится бюджетная линия в случае, если: а) размер стипендии вырастет до 300 руб.; б) при неизменности цены единицы питания, цена единицы развлечения снизится до 4 руб. б) определить оптимальный набор товаров для этого студента, если имеются данные по трем кривым безразличия для тех же двух товаров, что и в таблице 5.3. Координаты точек на кривых: Таблица 5.3.
4. а)Постройте кривые безразличия Алеши и Наташи для двух благ: арбузов и свиных хрящиков при условии, что Алеша любит свиные хрящики и не ест арбузов, а Наташа с удовольствием ест арбузы и ненавидит свиные хрящики. б) Построить кривые безразличия для двух абсолютно взаимозаменяемых товаров пепси-колы и кока-колы, если их цены за литр равны 8 и 10 руб. при бюджете на их потребление, равном 40 руб.
5. Потребитель А решает, каким образом распределить свой доход между покупкой грампластинок и одежды. Рисунок 5.1 показывает его бюджетную линию и кривую безразличия. Укажите на рисунке следующие точки: а) Точку, в которой А максимизирует свои потребности. б) Точку, в которой А покупает только грампластинки. в) Точку такого набора, выбрав который, А не израсходовал бы весь свой доход, предназначенный на покупку указанных товаров. г) Точку, в которой А получает то же удовлетворение, что и в точке d, новыходящее за пределы его бюджетных возможностей, д) Точку, в которой А покупает только одежду. е) Точку, отражающую более предпочтительный набор, чем тот, который представленточкой d, но выходящий за пределы бюджетных возможностей А.
Рис. 5.1. Кривая безразличия и бюджетная линия потребителя
6. Студент читает журналы и слушает музыку, записанную на кассеты. Таблица 5.4. показывает полезность, которую он получает от потребления различного количества журналов и кассет. Цена журнала – 1,5 долл., а цена кассеты – 7,5 долл. Предположим, что обычно студент покупает 2 кассеты и 10 журналов. Можете ли вы установить, максимизирует ли студент полезность?
Таблица 5.4.
7. Корзина потребителя состоит из двух товаров: А и Б. Цена на товар А повысилась с уровня Ра до уровня Ра1. Цена на товар Б осталась неизменной. Покажите графически разложение общего эффекта повышения цены на товар А на эффект замещения и эффект дохода по Хиксу, используя при этом рис. 5.2.
MN – бюджетная линия, соответствующая денежному доходу I и ценам Ра и Рб. UU – кривая безразличная. т. К – соответствует денежному доходу I и цене Ра1.
8. На рис.5.3. изображена ситуация равновесия потребителя при заданной бюджетной линии АВ. Предположим, что цена товара Х понизилась до уровня Рх1, при прочих равных условиях, что соответствует т. С на графике. Разложите общий эффект понижения цены на товар Х на эффект замещения и эффект дохода по Слуцкому и покажите это графически.
9. В равновесии рациональный индивид потребляет 2 кг помидоров по цене 3 руб. за 1 кг и 4 кг груш по цене 5 руб. за 1 кг. Чему равна для него предельная норма замены груш помидорами?
10. Потребитель тратит 20 руб. в день на апельсины и яблоки. Предельная полезность яблок для него равна 20 — 3х, где х — количество яблок, в шт. Предельная полезность апельсинов равна 40 — 5у, где у — количество апельсинов, в шт. Цена одного яблока составляет 1 руб., цена одного апельсина — 5 руб. Какое количество яблок и апельсинов купит рациональный потребитель?
11*. Кривая безразличия задана степенной функцией Оa = = 1/Qb2. Бюджетная линия касается кривой безразличия в точке Qb = 2. Доход потребителя I = 48. Найти Pa и Pb.
12*. Функции совокупной полезности потребителя от потребления благ А и В заданы уравнениями TUa = 16Qa – Qa2 и TUb = 20Qb — 1,5Qb2 Цена блага А (Рa) равна 2, блага В (Рb) равна 5, доход (I) равен 39. Найти: а) Какой объем благ А (Qa) и В (Qb) приобретет потребитель, чтобы максимизировать доступную ему совокупную полезность (TUmax)? б) Найти TUmax.
13. Цена товара А равна 12, цена товара В равна 5, доход равен 240. Найти объемы приобретенных товаров А и В, если известно, что покупатель приобрел товаров А в 4 раза меньше, чем В.
14. Кривая безразличия задана табличным способом. а) Заполните пустые клетки таблицы 5.5. б) Определите, как изменится полезность каждого набора, если в него добавить 0,5 единиц продукта X и 1 единицу продукта Y. Таблица 5.5.
Тема 6. Теория фирмы 1. Заполните таблицу 6.1. и начертите графики совокупного, среднего и предельного продуктов. Таблица 6.1.
2.* В производственном процессе величина капитала фиксирована: К = К0. Величина труда L — изменяется. Найдите взаимозависимости между трудом L, общим продуктом труда ТPL предельным продуктом труда МPL, и производительностью труда АPL, если известны следующие данные:
Таблица 6.2.
3. Даны 2 производственные функции предприятия, которое использует единственный фактор — труд: а) q = 10 L2 — 2 L3 б) q = 8L. Найдите функцию среднего и предельного продукта труда каждого производственного процесса.
4. На рис. 6.1. представлена карта изоквант с первоначальной изокостой АВ и новой изокостой АС. Фирма предполагает максимизировать прибыль и направляет 500 долл. на покупку ресурсов. Ответьте на вопросы: а) Какова первоначальная цена капитала? Как она определяется? б) Какова первоначальная цена труда? Как она определяется? в) Какова новая цена капитала? Как она определяется? г) Какова новая цена труда? Как она определяется? д) В какой точке фирма первоначально находится в состоянии равновесия? Почему? Сформулируйте правило минимизации издержек. е) Какова новая точка равновесия фирмы? Почему? ж) Напишите уравнения для изокосты АВ и изокосты АС. з) Каковы относительные значения МРk и МРL в точке «b»? Почему? и) Каковы относительные значения МРk и МРL в точке «а»? Почему? к) Может ли фирма находиться в точке «с»? Почему? В каком случае точка «с» окажется достижимой? л) Определите наклон линии АВ. м) Определите наклон линии АС. н) Как можно выразить наклон изокванты I0 в точке «а»?
Рис.6.1. Карта изоквант и изокосты 5. Дана производственная функция q = 5 * К * L. а) Цены труда и капитала равны: РL = 2 и РK = 1, располагаемый бюджет фирмы равен 100; определите оптимальную комбинацию К и L б) РL = 2 и PK = 1; найдите оптимальную комбинацию К и L при объеме производства q = 6250. в) Какова равновесная комбинация изокванты q = 6250, если значение отношения между РL /PK увеличится вдвое? г) Каково поведение фирмы в краткосрочном периоде с объемом фиксированного капитала, равным К0 = 50 при PL = 4 и PK = 1?
6. Производственная функция фирмы равна Q = K1/4 L3/4.Цена капитала равна 4 тыс. руб. Цена труда равна 12 тыс. руб. Какое количество капитала и труда должна иметь фирма для выпуска 300 тыс. единиц.
7. Заполните таблицу 6.3: Таблица 6.3.
8.* Фирма несет постоянные издержки 45 тыс. марок, а также средние переменные издержки, которые составляют следующие величины:
Таблица 6.4.
Определить и нарисовать все виды средних и предельных издержек.
9.* Заполните таблицу 6.5: Таблица 6.5.
10. Дана следующая функция общих издержек в краткосрочном периоде: TC (q) = q3 – 8q2 + 24q + 6 Определите функции общих средних и предельных издержек.
11. Каждая из четырех кривых краткосрочных средних общих издержек, указанных на рис. 6.2, представляет различный масштаб деятельности фирмы. а) Определите, какой объем выпуска продукции является для фирмы оптимальным? б) Если фирма увеличит масштаб деятельности за пределы оптимального, то каким окажется характер отдачи от масштаба? в) Какой из четырех масштабов производства был бы выбран, если бы фирма выпускала продукцию в объеме 0A? г) Если фирма расширит объем производства до ОВ, то как изменится масштаб деятельности фирмы в краткосрочном и долгосрочном периодах? д) Начертите кривую долгосрочных средних издержек фирмы.
12. Владелец фирмы выплатил наемным работникам 50 тыс. франков. Плата процентов за кредит составила 100 тыс. франков; амортизационные отчисления — 50 тыс. франков; затраты на сырье, отопление, освещение, ремонт и т. д. — 30 тыс. франков. Совокупный доход фирмы составил 300 тыс. франков. Владелец фирмы может сам устроиться на работу наемным работником в другую фирму и получать, там 60 тыс. франков. От вложений своего капитала в другое предприятие владелец фирмы мог бы получить 20 тыс. франков. Определите: а) бухгалтерские издержки; б) экономические издержки; в) бухгалтерскую прибыль; г) экономическую прибыль; д) следует ли владельцу фирмы продолжать свое дело.
13. Производственная функция фирмы имеет вид: q = L1/2 * K1/2 РL = 9 и PK = 4. Определить: а) функции издержек в долгосрочном периоде; б) функции издержек в краткосрочном периоде при K0 = 36.
14. Заполните таблицу 6.6. (при условии, что форма действует в условиях совершенной конкуренции, а FC = 16): Таблица 6.6.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2044; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.014 с.) |



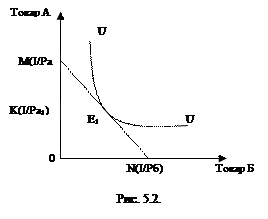


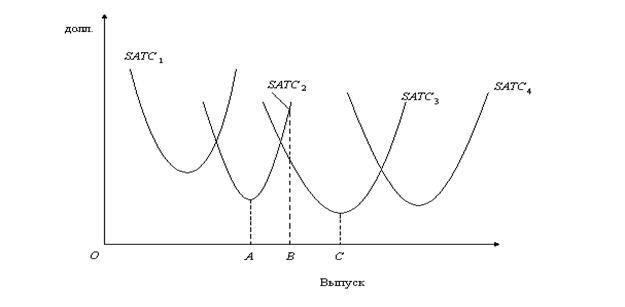 Рис. 6.2. Кривые средних издержек
Рис. 6.2. Кривые средних издержек


