
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы интегрирования дифференциальных уравнений: метод Эйлера и метод Рунге-Кутта.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прямой метод Эйлера - аппроксимируем производную в момент времени tk соотношением
Формула (2) известна как прямой метод Эйлера. На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(xk,tk).
На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(xk+1,tk+1).
4)Уравнения с разделенными и разделяющимися переменными. Дифференциальные уравнения с разделенными переменными
Однородные уравнения. Однородные уравнения – это уравнения вида k 0 xn + k 1 xn −1 y + k 2 xn −2 y 2+...+ kn −1 xyn −1+ knyn =0 k 0 x n + k 1 x n −1 y + k 2 x n −2 y 2+...+ k n −1 xy n −1+ k n y n =0 с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.151 (0.01 с.) |

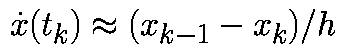 При такой аппроксимации уравнение (1) примет вид:
При такой аппроксимации уравнение (1) примет вид: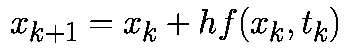
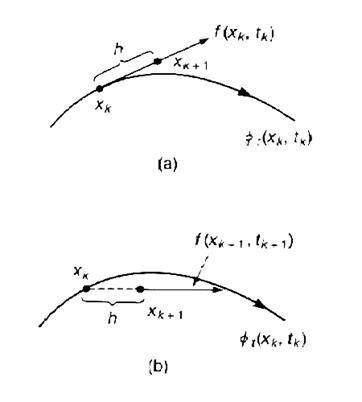 Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера. Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.
Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера. Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0. 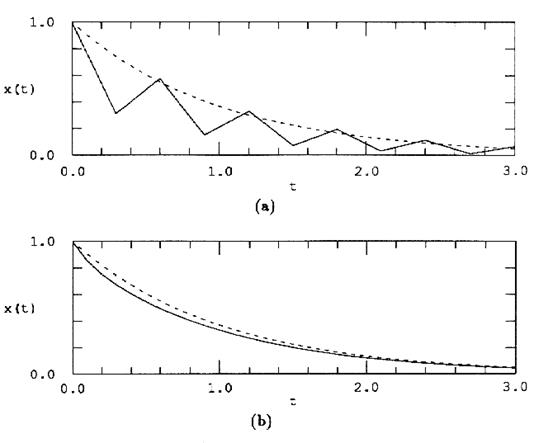
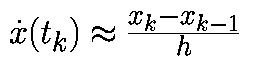 . Такая аппроксимация дает формулу обратного метода Эйлера:
. Такая аппроксимация дает формулу обратного метода Эйлера: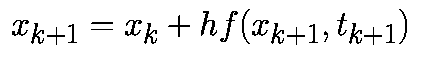
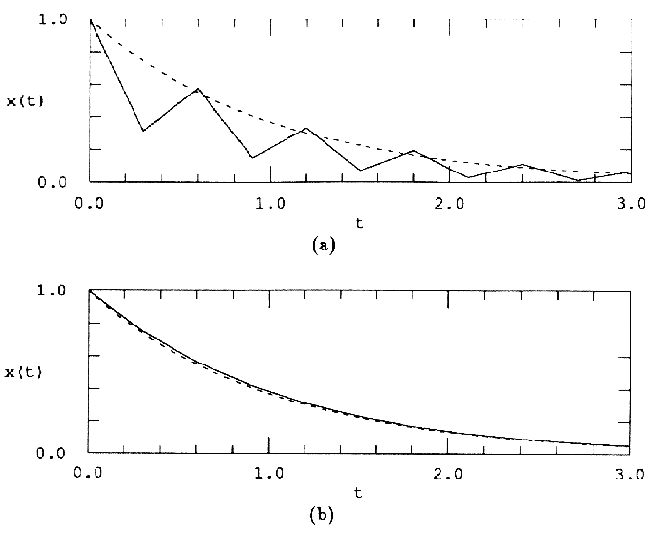 Рис.3 Та же система, что и на рис.2 проинтегрирована от x0=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией. Метод Рунге-Кутта - в основу семейства алгоритмов Рунге-Кутта положена идея аппроксимации фt(xk) рядом Тейлора. Рассмотрим алгоритмы второго и четвертого порядков. Термин "k-го порядка" означает, что в аппроксимации используется k членов ряда Тейлора. Метод Рунге-Кутта второго порядка -имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:
Рис.3 Та же система, что и на рис.2 проинтегрирована от x0=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией. Метод Рунге-Кутта - в основу семейства алгоритмов Рунге-Кутта положена идея аппроксимации фt(xk) рядом Тейлора. Рассмотрим алгоритмы второго и четвертого порядков. Термин "k-го порядка" означает, что в аппроксимации используется k членов ряда Тейлора. Метод Рунге-Кутта второго порядка -имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением: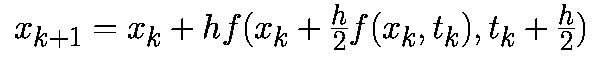 Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (tk+h/2):
Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (tk+h/2):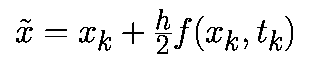 На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:
На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа: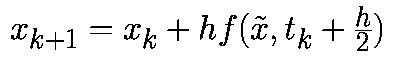 Модифицированный алгоритм Эйлера-Коши использует значение векторного поля в средней точке между xkи xk+1. Он отличается от трапецеидального алгоритма, в котором используется среднее значение векторного поля по xk и xk+1. Его можно рассматривать как явный алгоритм, который, используя промежуточный шаг по времени, включен в неявный алгоритм. Метод Рунге-Кутта четвертого порядка - как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени tk+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:
Модифицированный алгоритм Эйлера-Коши использует значение векторного поля в средней точке между xkи xk+1. Он отличается от трапецеидального алгоритма, в котором используется среднее значение векторного поля по xk и xk+1. Его можно рассматривать как явный алгоритм, который, используя промежуточный шаг по времени, включен в неявный алгоритм. Метод Рунге-Кутта четвертого порядка - как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени tk+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка: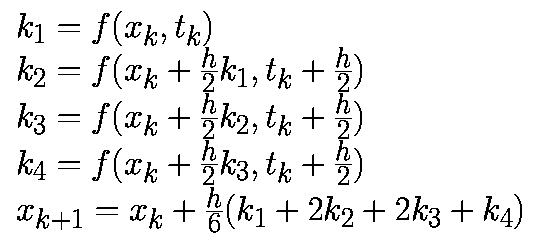
 .
.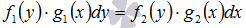 .
.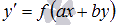 , a ≠ 0, b ≠ 0.
, a ≠ 0, b ≠ 0. 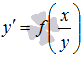 или
или 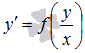 .
. .
.


