Отношения пас по логическому квадрату. Умозаключения по логическому квадрату. Основные принципы классической логики с точки зрения пас.

 

 

А противоположость E

контрарность

под

чине

ние

(суб

орд

инация) отношение противоречия

контрадикторность.

 

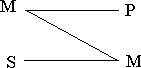
I частичная совместимость O

субконтрарность

Буквы символизируют различные виды суждений. Его стороны и диагонали выражают всю совокупность возможных отношений между ними. Линия AE образует отношение противоположности или контрарности. Пары этих суждений не могут быть одновременно истинными. Могут быть оба ложными, одно истинным, а другое ложным.

Две расположенные по диагонали пары AO и EI составляют отношение противоречия или контрадикторности. Истинностные значения регулируются законно исключенного третьего: когда одно истинно, другое ложно.

Нижняя сторона квадрата выражает отношение частичной совместимости или субконтрарности. Эта пара никогда не бывает одновременно ложной. Когда одно из них ложно, другое обязательно истинно, о другом ничего сказать нельзя. Могут быть оба истинны.

Стороны AI и EO выражают отношение подчинения или субординации. Истинность общего суждения выражает одновременно истинность частного.

 

Умозаключения по логическому квадрату.

 

Непосредственные умозаключения из ПАС (обращение, превращение).

Умозаключение называется непосредственным, если оно состоит из одной посылки и заключения.

Превращение – логическая операция, изменяющая качество суждения без изменения его количества.

при превращении квантор и субъект остаются теми же самыми, но связка меняется на противоположную, а предикат заменяется на дополнение к нему, т.е. P заменяется на не-P. Происходит своеобразное двойное отрицание – связки и предиката.

Превращение осуществляется двумя способами:

А) путем двойного отрицания, которое ставится перед связкой и предикатом:

S есть P à S не есть не-P.

Б) путем перевода отрицания из предиката в связку:

S есть не-P à S не есть P.

SaPàSeP’

SePàSaP’

SiPàSoP’

SoPàSiP’

 

Обращение – операция перестановки субъекта суждения и предиката местами без изменения качества суждения.

Обращение подчиняется правилу распределенности терминов: субъект распределен в общих и не распределен в частных суждениях, предикат распределен в отрицательных и не распределен в утвердительных суждениях.

Различаются два вида обращения: чистое обращение, когда количественная меняется на не- нтор и субъект остаются теми же самыми, но связка меняется на противоположную, а предикат заменяется на дополхарактеристика высказывания не изменяется, и обращение с ограничением, когда количественная характеристика изменяется.

SeP и SiP – обращаются чисто

SaP – обращается с ограничением.

SoP – не обращается.

SaP àPiS (SaPàPaS)

SePàPeS

SiPàPiS (SiPàPaS)

Простой категорический силлогизм (ПКС). Термины и посылки ПКС. Понятие фигуры и модуса ПКС. Общие правила ПКС.

Категорический силлогизм – это дедуктивное умозаключение, в котором из двух категорических высказываний выводится новое категорическое высказывание.

В каждом силлогизме должно быть три термина: больший, меньший и средний.

Больший термин - предикат заключения. (Р)

Меньший термин – субъект заключения. (S)

Средний термин – присутствует в обеих посылках, но отсутствует в заключении. (М)

Условившись всегда помещать большую посылку на первое место, а под ней записывать меньшую посылку, можно все простые категорические силлогизмы разделить по фигурам.

Фигура - это структура простых категорических силлогизмов, определяемая расположение среднего термина посылка.

1.М – Р

\

2. S – M

-----------

3. S - P

Фигура 1.

1. P – M

|

2. S – M

-----------

3. S - P

Фигура 2.

1. М– P

|

2. М– S

-----------

3. S - P

Фигура 3.

1. P – M

/

2. М – S

-----------

3. S - P

Фигура 4

Посылками и заключениями силлогизмов могут быть категорические суждения четырех видов: SaP – общеутвердительные суждения, Sip – частные утвердительные суждения, SeP – общеотрицательные суждения, SoP – частные отрицательные.

Модусами силлогизма называются разновидности фигур, отличающихся характером посылок и заключения.

Модусы, для которых между посылками и заключение существует отношение логического следования, называются правильными. Только в первой фигуре есть модусы всех суждений в заключении. Модусы первой фигуры интуитивно понятны, поэтому первая фигура совершенна.

Фигура 1.

Barbara (aaa)

Celarent (eae)

Darii (aii)

Ferio (eio)

Barbari (aii)

Celaront (eao)

 

Фигура 2.

Baroko (aoo)

Cesare (eae)

Camestres (aee)

Festino (eio)

Camestrop (aea)

Cesaro (eao)

 

Фигура 3.

Bokardo (oao)

Disamis (iai)

Datisi (aii)

Ferison (eio)

Darapti (aai)

Felapton (eao)

 

Фигура 4.

Bramantip (aai)

Dimaris (iai)

Camenens (aae)

Camenos (aeo)

Fesapo (eao)

Fresison (eio)

 

 

Общие правила ПКС.

I. Правила терминов:

1) в силлогизме должно быть только 3 термина

Термин М должен быть одним и тем же понятием в обеих посылках, иначе получим ошибку, называемую "учетверением терминов".

2) средний термин должен быть распределен хотя бы в одной из посылок.

Если средний термин не распределен ни в одной из посылок, то отношение между крайними терминами в заключении остается неопределенным.

3) термин, не распределенный в посылках, не может быть распределен в заключении.

При нарушении этого правила возникает лог. ошибка "незаконное расширение термина".

II. Правила посылок:

1) Из двух отрицательных посылок заключение сделать нельзя (хотя бы одна из посылок должна быть утвердительной).

2) Из двух частных посылок заключение не следует (хотя бы одна из посылок должна быть общим суждением).

Из двух частных посылок правильное заключение сделать невозможно.

3) если одна из посылок - отрицательное суждение, то и заключение должно быть отрицательным.

4) если одна из посылок частная, то и заключение должно быть частным.

I фигура ПКС.

I фигура

В 1-й фигуре средний термин занимает место субъекта в большей посылке предиката в меньшей.

Пример:

Все металлы (М) - электропроводны (Р)

Медь (S) - металл (М)

Медь (S) - электропроводна (Р)

Правила 1-й фигуры:

1) бoльшая посылка должна быть общей (А или Е);

2) мeньшая посылка должна быть утвердительной (А или I).

 

 

II фигура ПКС.

II фигура

Во 2-й фигуре средний термин занимает место предиката в обеих посылках

Пример:

Этот смертельный удар (Р) нанесен человеком огромной силы (M)

Обвиняемый (S) не является человеком огромной силы (М)

Обвиняемый (S) не нанес этот смертельный удар (P)

Правила 2-й фигуры:

1) бoльшая посылка должна быть общим суждением (А, Е);

2) одна из посылок должна быть отрицательным суждением (E, I).

III фигура ПКС.

III фигура

В 3-ей фигуре средний термин занимает место субъекта в обеих посылках.

Пример:

Ни один страус (М) не летает (Р)

Все страусы (М) птицы (S)

Некоторые птицы (S) не летают (P)

Правила 3-й фигуры:

1) мeньшая посылка должна быть утвердительным суждением (А, I);

2) заключение должно быть частным суждением (I, О).

IV фигура ПКС.

IV фигура

В 4-й фигуре средний термин занимает место предиката в большей и субъекта в меньшей посылке.

Пример:

Ни один счастливый человек(Р) не стремится к справедливости (М)

Некоторые стремящиеся к справедливости люди (M) являются юристами (S)

Некоторые юристы несчастны