
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Язык науки и язык человеческий.Содержание книги
Поиск на нашем сайте
Приходится лишь сожалеть, что язык современной математики настолько усложнен и специализирован, что ее результаты доступны только весьма узкому кругу специалистов [60, VIII ]. В. Сойфер.
«Сомнительность» математических доказательств, - пишет Гегель, - «могла бы быть устранена только посредством объяснения. Но тогда существенным выражением мысли явится это объяснение и математическая символика окажется бессодержательным излишеством» [9, 57-58]. «Бессодержательное излишество» этой символики состоит в том, что ее невозможно использовать для объяснения ибо
объяснение есть согласование с уже объясненным,
а это возможно лишь в рамках единого языка.
«Рано или поздно физики захотят сообщить о своих достижениях нефизикам, и этот рассказ придется вести обычным языком. Это значит, что для интерпретации математической схемы понадобится языковая модель» [14, 26]. Фритьоф Капра. Дело, конечно, не в том, захотят физики сообщить о своих достижениях, или не захотят, - придется «захотеть», - согласование теорий есть необходимый этап в развитии научного знания. И как бы не была научная деятельность специализирована, но запереть ее в сфере науки невозможно, - самой науке не избежать ни обращения к практике, ни сопоставления с данными тысячелетнего, обыденного опыта человечества. Опыта, на котором одном только и держится здравый смысл, но с ним общаться можно лишь на языке чувственных, осязаемых образов, - не математических символов. Примечательно, что вопрос о едином языке науки ставится сегодня именно со стороны физиков-теоретиков. А. Липкин, например, в книге «Модели современной физики» отстаивает положение о ведущей роли в физике модельного слоя. Более того, он этот слой выделят как общий для всех разделов физики [4, 21], недвусмысленно говоря, что именно модель, образ изучаемого процесса является в науке языком общения. Любая гипотеза, претендующая на статус теории, проходит как бы экзамен на соответствие теориям, которые этот экзамен уже прошли. Упреки теории всемирного тяготения, как и теории относительности в отсутствии модельного слоя есть по сути признание, что данные гипотезы не только экзамена не прошли, но к нему и не допускаются. Из-за незнания языка.
* Выделено мною, - Л.Ф.
[1] Конспектируя Гегеля, Ленин запишет: «В примечании у Гегеля, как и всегда, фактическое, примеры, конкретное (Фейербах поэтому смеется однажды, что Гегель природу сослал в примечания…)» [11, 112]. [2] Став светилами науки, они обращаются с этой бесконечностью запанибрата, но стал ли этот математический символ для них понятием, или они просто им «привыкли пользоваться», - вопрос, во всяком случае, дискуссионный.
[3] О «квадратном трехчлене», - ни слова!
* Имеется в виду письмо Г. В. Фабиана Марксу от 6 ноября 1880 г. О * Тем, кто не улыбнулся при упоминании имени полковника, автор от души советует перечитать главу «Катастрофа» из «Похождений бравого солдата Швейка». Узнаете, кстати, что такое канава? * Рафаил Нудельман сегодня пишет об ученых, которые «пользуются математикой, «которая работает даже там, где воображение уже отказывает». И постепенно привыкают. Когда некий студент пожаловался своему научному руководителю, что не понимает выражения «пространственное распределение вероятности», тот ответил: «Это не нужно понимать, нужно привыкнуть этим пользоваться» [56, 25].
[4] Энгельс. * Душу согрели автору рассуждения Рафаила Нудельмана по поводу перехода от Стандартной модели к Суперсимметрии: «Новым поколениям студентов придется переучиваться, а кое-кому из стариков – так и остаться в вечных неладах с новыми теориями, как когда-то с квантовой механикой и теорией относительности. Только нам, дилетантам, и изначально не знавшим ни той, ни другой модели, будет хорошо и просто – так же хорошо и просто, как тому покупателю на одесском базаре, который в ответ на свою тихую просьбу: «Мне, пожалуйста, без сиропа», услышал от продавщицы бессмертный вопрос: «Вам без какого сиропа – без яблочного или без апельсинового?» [70, 57].
* Ребята – фэ-эм-шата, - ученики физико-математических (ФМ) школ. Автору посчастливилось там преподавать, - чудесный народ. Гегелей бы им еще в педагоги.
* В нервно-физиологическом плане интуиция как раз и базируется на ассоциативных связях с самыми отдаленными пластами знания, казалось бы, к рассматриваемому процессу отношения не имеющими. Чтобы мышление уже на уровне подсознания свободно эти пласты пронизывало и столь же свободно в них ориентировалось, все человеческое знание (а знание есть способ, которым существует сознание, – Маркс), несомненно, должно быть закодировано единым способом.
* * Под «обычным языком» Фритьоф Капра и имеет в данном случае язык моделей. Выделено мною, - Л.Ф.
[5] По поводу книги Томсона и Тейта «Трактат о натуральной философии» [6, 72].
* Углубляться в этот вопрос в данной работе просто не представляется возможности, - это самостоятельная тема. [i] Фритьоф Капра, - современный философ и физик-теоретик. Книга «Дао физики» (1976). Для преодоления теоретических проблем вызванных парадоксальной природой открытий в области ядерной физики и квантовой механики, Ф. Капра пытается применить интуитивно-созерцательный подход, характерный для философских учений Востока. Позиция Ф. Капра о соотношении в научном исследовании математического и модельного методов во многом переплетается с взглядами по этому вопросу Гегеля и Энгельса.
[ii] В подготовительных работах к «Диалектике природы» среди материалов посвященных математике имеется у Энгельса и набросок статьи, - «О прообразах математического бесконечного в действительном мире» [6, 231-237].
[iii] Гегель проводит основательный разбор математических рассуждений Ньютона, с указанием и анализом многочисленных ошибок именно в сфере перевода математических абстракций в физическую реальность, что автор опускает. Раздел посвященный математике и так смещен к научно-теоретическому. Для интересующихся, - Гегель. Наука логики. т. 1. Раздел «Величина (количество)». Большая Логика, а не первый том Энциклопедии, - так наз. Малая Логика.
|
||||||
|
Последнее изменение этой страницы: 2022-09-03; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.101.51 (0.01 с.) |

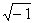 Энгельс говорит в XII главе первого отдела «Анти-Дюринга» [26, 120-121].
Энгельс говорит в XII главе первого отдела «Анти-Дюринга» [26, 120-121].


