
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что называется поперечной силой, ее знакиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Что называется поперечной силой, ее знаки Поперечная сила Q в сечении равна алгебраической сумме проекций всех сил, действующих по одну сторону сечения, на нормаль к оси стержня. Поперечная сила считается положительной, если вращает отсеченную часть по часовой стрелке. Характер изменения эпюры Q связан с известной дифференциальной зависимостью с изгибающим моментом: Следовательно: – на ненагруженном участке эпюра Q постоянна; – на участке, где действует равномерно распределенная нагрузка, эпюра Q линейна. Нулевому значению поперечной силы отвечает экстремальное значение изгибающего момента; – в месте приложения сосредоточенной силы в эпюре Q будет скачок на величину этой силы.
Что называется продольной силой, ее знаки Центральным растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила N. Правило знаков для продольной силы: если продольная сила N направлена от сечения (растяжение), то она положительна, если к сечению (сжатие) - то отрицательна. Продольная сила определяется с помощью метода сечений
Общий порядок проведения кинематического анализа Порядок и процедуры кинематического анализа В ходе кинематического анализа расчётной схемы сооружения даются ответы на два главных вопроса: 1) достаточно ли суммарное число внешних и внутренних связей в системе для того, чтобы при правильном их размещении обеспечить её геометрическую неизменяемость? 2) правильно ли расставлены связи? Следует обратить внимание на то, что первый вопрос ещё не предполагает изучения правильности расстановки связей – он нацелен на оценку их количества. В связи с этим в кинематическом анализе выделяются два последовательных этапа: 1) количественный анализ; 2) качественный (структурный) анализ. К о л и ч е с т в е н н ы й а н а л и з – это исследование расчётной схемы сооружения, заключающееся в оценке баланса (соотношения) суммарного числа степеней свободы дисков системы до наложения на них внешних и внутренних связей (т.е. несвязанных дисков) и суммарного числа внешних и внутренних связей системы, в пересчёте на связи первого типа. Указанный пересчёт объясняется тем, что именно связь первого типа способна устранять, при правильном её использовании, одно возможное взаимное перемещение (линейное или угловое) соединяемых дисков, т.е. одну степень свободы. К а ч е с т в е н н ы й (с т р у к т у р н ы й) а н а л и з – это исследование структуры расчётной схемы сооружения, заключающееся в проверке правильности расположения связей, выявлении возможных дефектов соединения дисков и завершающееся определением кинематического качества (природы) системы (её геометрической неизменяемости, изменяемости или мгновенной изменяемости). В ходе структурного анализа дается оценка кинематического качества каждой внешней и внутренней связи на основании упоминавшегося выше кинематического признака классификации связей. По этому признаку классифицируются только простые (линейные и угловые) связи, которые подразделяются на необходимые, лишние и ложные. Имеющиеся в системе сложные связи (шарниры, припайки) предварительно представляются как соответствующие комбинации простых связей. А)Определение усилий в стержнях фермы построением диаграммы Максвелла-Кремоны. Это графический способ расчета усилий в стержнях фермы. Построение диаграммы Максвелла-Кремоны заключается в построении силовых многоугольников, построенных для всех узлов фермы, в один чертеж так, чтобы ни одно из усилий не повторялось дважды (рис. 3). При расчете фермы способом Максвелла-Кремоны следует придерживаться следующей последовательности действий: 1.Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело. 2.Отбросить опоры и изобразить все приложенные к ферме внешние силы, включая реакции опор, так чтобы эти векторы располагались вне контура фермы. 3.Части плоскости, ограниченные контуром фермы и линиями действия внешних сил, а так же те, что ограниченны стержнями фермы, обозначить буквами; узлы обозначить римскими цифрами, стержни - нумеруем арабскими. 4.Построить замкнутый многоугольник внешних сил, откладывая силы в том порядке, в котором они встречаются при обходе фермы (направление произвольно) силы обозначаются малыми буквами, соответствующими обозначениям смежных участков плоскости. 5.Последовательно, на том же рисунке, построить силовые многоугольники для каждого узла (узлы выбираются таким образом, чтобы число неизвестных усилий в стержнях равнялось двум), направление обхода узла должно совпадать с направлением обхода плоскости. 6.Стержень считать сжатым, если направление, указанное известными силами, направлено к узлу, в противном случае стержень растянут. 7.Измерить на диаграмме отрезки, изображающие искомые усилия в стержнях фермы, и найти усилия, учитывая принятый масштаб сил.
Б)Определение усилий в стержнях фермы методом сечений (методом Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, например, для проверочных расчетов (рис. 4) При расчете методом сечении рекомендуется такая последовательность действии: 1. Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело, находящееся под действием плоской системы сил. 2.Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е., считая их растянутыми. 3.Затем составляются уравнения равновесия так, чтобы в каждое уравнение входило одно неизвестное усилие. 4.Из полученных уравнений находятся неизвестные усилия в стержнях; если в ответе получается знак «-», то это означает, что стержень сжат, а не растянут.
Перемещения,их обозначения Перемещения в строительной механике, линейные отклонения точек конструкции, углы поворота сечений, а также комбинации этих величин (взаимные смещения), характеризующие изменение положения конструкции под влиянием силовых нагрузок, температурных воздействий или осадки опор. П. определяют: при оценке жёсткости и связанных с ней эксплуатационных качеств конструкций; как вспомогательные величины при расчёте статически неопределимых систем; при расчёте устойчивости и колебаний конструкций. В стержневых системах для определения П. обычно пользуются формулой Мора; при этом в общем случае учитывают зависимость П. от изгибающих моментов, продольных и поперечных сил, возникающих в элементах системы под влиянием действующих нагрузок, а в частных случаях учитывают влияние либо только изгибающих моментов (в балках, рамах), либо только продольных сил (в фермах). Метод перемещений является вторым основным методом расчета статически неопределимых систем. Использование его для расчета сложных статически неопределимых рам во многих случаях значительно снижает трудоемкость расчета по сравнению с методом сил. Общее число неизвестных при расчете статически неопределимых систем определяется не статической, а кинематической неопределимостью. При этом род степенью кинематической неопределимости понимается число угловых и линейных перемещений системы, знание которых дает возможность определить характер деформации системы, а следовательно, и усилия в ее элементах. Деформированный вид системы будет полностью определен, если будут известны угловые и линейные перемещения узлов системы. Степень кинематической неопределимости системы будет равна числу углов поворота жестких узлов плюс число неизвестных линейных перемещений узлов. Для многих статически неопределимых систем степень кинематической неопределимости ниже их степени статической неопределимости. В основу метода перемещений положен ряд допущений: не учитывается влияние поперечных и продольных сил на перемещения точек системы; не учитывается сближение узлов системы при деформации ее элементов; концы стержней, сходящихся в одном жестком узле, поворачиваются при деформации на один и тот же угол; углы поворота вследствие их небольшой величины принимаются равными тангенсам этих углов. Формула Мора Универсальный метод определения перемещений (линейных перемещений и углов поворота), возникающих в любой стержневой системе от произвольной нагрузки, имеет особенно большое значение для расчета статически неопределимых систем.
Рассмотрим два состояния системы. В первом состоянии на нее действует любое число каких угодно сил и моментов (рис. 5.14, а). Во втором состоянии к системе приложена одна лишь сосредоточенная сила Р2=1(рис. 5.14, б). Составим выражение работы А21 силы Р2=1 на перемещении а21возникающем от сил первого состояния:
Выразим А21 (в случае плоской задачи) через внутренние усилия в стержнях системы [с помощью формул (5.17) и (5.20)]:
Условимся, что черточки над М2, N2, Q2,указывают на то, что эти внутренние усилия вызваны действием силы, равной единице. Таким образом, перемещение от любой нагрузки с помощью формулы (5.22) можно выразить через внутренние усилия, возникающие в заданной системе от этой нагрузки и возникающие в ней от единичной силы. Направление единичной силы совпадает с направлением определяемого перемещения. Если определяется линейное смещение (например, прогиб какой-либо точки оси стержня), то единичная сила представляет собой безразмерную сосредоточенную силу, приложенную в этой точке; если же определяется угол поворота поперечного сечения в какой-либо точке оси стержня, то единичная сила представляет собой сосредоточенный момент (также безразмерный), приложенный в этой точке. Состояние сооружения, вызванное действием единичной силы, называется единичным состоянием (или фиктивным). В отличие от него состояние, вызванное действием заданной нагрузки, называется действительным (или грузовым). Иногда цифровые индексы 1 и 2 в формуле (5.22) заменяются буквенными, например m и n, тогда эта формула принимает вид
где аmn— перемещение по направлению «силы» P=1 вызванное действием нагрузки n(группы «сил»n). При размерах поперечных сечений каждого стержня системы, постоянных по длине этого стержня, выражение (5.23) принимает вид
Каждое из равенств (5.22) — (5.24) носит название формулы перемещений (интеграла, или формулы, Мора).
Сущность метода сил метод сил заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Алгоритм расчета методом сил: Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил: 1. Определить степень статической неопределимости. 2. Выбрать основную систему. 3. Сформировать эквивалентную систему. 4. Записать систему канонических уравнений. 5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции. 6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений. 7. Построить суммарную единичную эпюру. 8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов. 9. Решить систему канонических уравнений, т.е. определить реакции лишних связей. 10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры). 11. Выполнить статическую и кинематическую проверки. Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной. Основные этапы раскрытия статически неопределимых систем по методу сил: 1.Определить степень статически неопределимой системы, то есть число лишних неизвестных. 2.Удаляем лишние связи и заменяем т.о. исходную статическую неопределимую систему на определимую (освобождённая от лишних связей называется основная). Нужно следить за тем,чтобы основная система оставалась геометрически неизменяемой т.е её элементы после удаления лишних связей не должны иметь возможности свободно перемещаться в пространстве. 3.Составляем уравнения для деформаций в точках приложения лишних неизвестных т.к в исходной системе эти деформации равны 0, то и указанные уравнения необходимо также приравнять к 0, затем из полученных уравнений находим величину лишних неизвестных.
ПРАВИЛО ВЕРЕЩАГИНА Вычисление интеграла Мора целесообразно вести по правилу, предложенному А. Н. Верещагиным в 1925 г. для прямолинейных брусьев.
Произведение
Таким образом, правило Верещагина состоит в том, что интеграл Мора, составленный для каждого из участков нагружения балки, равен произведению площади
Что называется поперечной силой, ее знаки Поперечная сила Q в сечении равна алгебраической сумме проекций всех сил, действующих по одну сторону сечения, на нормаль к оси стержня. Поперечная сила считается положительной, если вращает отсеченную часть по часовой стрелке. Характер изменения эпюры Q связан с известной дифференциальной зависимостью с изгибающим моментом: Следовательно: – на ненагруженном участке эпюра Q постоянна; – на участке, где действует равномерно распределенная нагрузка, эпюра Q линейна. Нулевому значению поперечной силы отвечает экстремальное значение изгибающего момента; – в месте приложения сосредоточенной силы в эпюре Q будет скачок на величину этой силы.
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1900; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.112 (0.011 с.) |



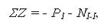 (сжатие, т.е. продольная сила направлена в противоположную сторону)
(сжатие, т.е. продольная сила направлена в противоположную сторону)

 Рис. 5.14
Рис. 5.14



 и
и  , входящие в формулу интеграла Мора, - это некоторые функции от х:
, входящие в формулу интеграла Мора, - это некоторые функции от х:  ,
,  , а графики этих функций - эпюры
, а графики этих функций - эпюры  на некотором участке балки. Причем если первая функция
на некотором участке балки. Причем если первая функция 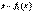 может быть и нелинейной, то вторая
может быть и нелинейной, то вторая 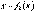 , выражающая изгибающий момент от единичной силы (или единичного момента), обязательно линейная. Поэтому ее можно представить уравнением прямой с угловым коэффициентом, т. е.
, выражающая изгибающий момент от единичной силы (или единичного момента), обязательно линейная. Поэтому ее можно представить уравнением прямой с угловым коэффициентом, т. е. .
. можно заменить вычислением интеграла
можно заменить вычислением интеграла .
.

 есть не что иное, как заштрихованная на рисунке 1 элементарная площадка эпюры
есть не что иное, как заштрихованная на рисунке 1 элементарная площадка эпюры  . Значит, первый интеграл в правой части равенства выражает площадь эпюры
. Значит, первый интеграл в правой части равенства выражает площадь эпюры  в интервале от х=0 до x=l, а второй интеграл - статический момент этой же площади относительно оси у, который, как известно из формулы, выражается произведением площади на координату
в интервале от х=0 до x=l, а второй интеграл - статический момент этой же площади относительно оси у, который, как известно из формулы, выражается произведением площади на координату  ее центра тяжести С. Если площадь эпюры
ее центра тяжести С. Если площадь эпюры  обозначить буквой
обозначить буквой  , то равенство примет вид
, то равенство примет вид ,
, , т. е. ордината эпюры
, т. е. ордината эпюры  . Следовательно, в окончательном виде
. Следовательно, в окончательном виде .
. .
. нелинейной эпюры изгибающих моментов
нелинейной эпюры изгибающих моментов  эпюры изгибающего момента
эпюры изгибающего момента  , соответствующую положению центра тяжести площади
, соответствующую положению центра тяжести площади  .
. -единичной.
-единичной.


