
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многопериодная модель потребленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим многопериодную модель. Будем считать, что налоги и трансферты отсутствуют и в результате доход совпадает с располагаемым доходом. Пусть доход потребителя (доход, не связанный с активами) в периоде t равен Yt. Будем считать, что потребитель имеет (до начала первого периода) первоначальные активы B0 (наследство). Пусть потребитель может свободно занимать и давать взаймы по одинаковой номинальной ставке процента (1) Напомним, что под сбережениями индивидуума мы понимаем ту часть совокупного дохода, которая не потребляется. Совокупный доход периода t в нашем примере состоит из дохода, не связанного с активами, Yt, и процентам по активам предыдущего периода rBt-1. Таким образом, сбережения периода t равны (2) Подставляя (2) в (1) после преобразований получаем, что изменение активов, в свою очередь, равно сбережениям: Многопериодное бюджетное ограничение. Рассмотрим двухпериодную модель и предположим для простоты, что потребитель не обладает никакими первоначальными активами (то есть В0=0) и не планирует оставлять наследство в конце жизни (В2=0). Тогда сбережения первого периода составят: (3) а сбережения второго периода равны: (4) Поскольку первоначальные активы отсутствуют, то (5) C1(1+r)+C2=Y1(1+r)+Y2 В рассматриваемой модели потребление в разные периоды времени играет роль разных товаров, и мы имеем стандартное бюджетное ограничение, где в левой части стоят расходы, а в правой – доходы потребителя: Бюджетное ограничение, записанное таким образом, называют ограничением, приведенном к будущему (второму) периоду, поскольку сегодняшние величины доходов и расходов записываются с поправкой на процент, который они могут принести в следующем периоде. Поделив левую и правую часть ограничения (5) на (1+r), мы получим бюджетное ограничение в терминах стоимости, приведенной к начальному моменту времени. Заметим, что, если бы потребитель имел (до начала первого периода) первоначальные активы B0 и собирался в конце второго периода оставить наследство своим потомкам, равное величине B2, то бюджетное ограничение приняло бы следующий вид: (6) C1(1+r)+C2= B0(1+r)2+Y1(1+r)+Y2 -B2 Описав бюджетное ограничение, перейдем к предпочтениям потребителя. Будем считать, что предпочтения потребителя описываются функцией полезности, зависящей от потребления в настоящем и в будущем периодах: u(C1, C2). Итак, потребитель решает стандартную задачу максимизации полезности при бюджетном ограничении: max u(C1, C2) C1(1+r)+C2=Y1(1+ r)+Y2
Решение этой задачи несложно изобразить графически (смотри Рис.1). Рис 1. Графическое представление двухпериодной модели потребления
От каких же параметров зависит текущее потребление, то есть оптимальное потребление первого периода? В первую очередь оптимальное потребление зависит от доходов, причем, как мы видим, текущее потребление зависит не только от текущего дохода Y1 , но и от будущего дохода Y2. Если мы будем считать потребление в каждом периоде нормальным товаром (что представляется разумным в сильно агрегированной экономике), то рост доходов будет способствовать и росту потребления. Другим фактором, влияющим на текущее потребление, является наклон бюджетной линии, определяемый ставкой процента. Как же изменится потребление с изменением процентной ставки? Следует отметить, что процентная ставка в рассматриваемой модели играет роль цены и ее изменение влечет соответственно два эффекта: эффект замещения и эффект дохода. Если ставка процента растет, то сегодняшнее потребление становится дороже, что вынуждает потребителя сокращать текущее потребление С1 и увеличивать будущее потребление С2. С эффектом дохода все не так однозначно, как с эффектом замещения, поскольку знак эффекта дохода зависит от типа потребителя: Если мы имеем дело с чистым заемщиком, то есть с потребителем, который в первом периоде потребляет больше своего дохода (С1*>Y1), то он проигрывает от повышения процентной ставки, так как увеличиваются проценты выплаты по кредиту, который он взял в первом периоде и, следовательно, его доходы уменьшаются, что и ведет к сокращению текущего потребления. В случае с чистым кредитором (то есть, с потребителем, который в первый период потребляет не весь свой доход, а остаток сберегает) ситуация выглядит иначе. Он выигрывает от повышения процентной ставки, так как ему возвращают долг с более высокими процентами, в результате его доходы возрастают, и увеличивается текущее потребление. Рассмотренные выше рассуждения можно получить формально из уравнения Слуцкого для случая натурального дохода:
Первое слагаемое в правой части отражает эффект замещения и является отрицательным, а второе слагаемое соответствует эффекту дохода и, как, следует из уравнения знак этого слагаемого зависит от соотношения между текущим потреблением и доходом, то есть, от того является ли потребитель заемщиком или же кредитором. Итак, мы можем заключить, что для заемщика рост ставки процента отрицательно влияет на текущее потребление, поскольку эффект замещения и эффект дохода действуют в одном направлении. В случае чистого кредитора влияние ставки процента на потребление в первом периоде неоднозначно: потребление падает, если доминирует эффект замещения, и растет, если доминирует эффект дохода. Что же можно заключить о влиянии ставки процента на совокупное потребление? Если предположить, что в процессе агрегирования эффекты дохода для кредиторов и заемщиков уничтожаются, то останутся лишь эффекты замещения, которые ведут к падению текущего потребления в результате роста процентной ставки.
Теория жизненного цикла Согласно теории жизненного цикла жизнь можно разделить на несколько периодов, которые характеризуются разными уровнями доходов. Для того чтобы можно было использовать двухпериодную модель потребления, рассмотренную выше, условно разделим жизнь на два периода: первый период будет соответствовать тому времени, когда человек работает и получает высокий доход, а второй период- время, когда человек на пенсии и имеет низкий доход.
Потребление базируется на ожидаемом жизненном доходе (богатстве). Учитывая стремление людей поддерживать неизменный уровень потребления, они сберегают в молодости (когда имеют высокий уровень дохода) и тратят эти сбережения в старости, как это показано на рисунке 2. Соответственно, накопленные активы достигают максимальной величины перед выходом на пенсию и затем равномерно тратятся до конца жизни. В терминах двухпериодной модели потребления, если потребитель начинает свою жизнь без каких-либо первоначальных активов, то богатство, подсчитанное в период 1 (W1), представляет собой приведенную стоимость доходов: Учитывая стремление потребителя сглаживать траекторию потребления (то есть поддерживать одинаковый уровень потребления при изменяющемся доходе) мы находим, что в двухпериодной модели имеет место следующая зависимость между потреблением и богатством:
то есть каждый период мы потребляем некоторую долю от совокупного богатства, причем эта доля зависит от ставки процента. В модели с большим количеством периодов этот коэффициент меньше, поскольку богатство должно быть распределено на большее число лет. Таким образом, чем больше лет надеется еще прожить данный человек, тем меньшую долю богатства он будет потреблять каждый год. Отсюда мы получаем, что предельная склонность к потреблению у молодых должна быть ниже, чем у старших поколений.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.170 (0.009 с.) |

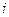 , причем (ожидаемая) реальная ставка процента одинакова для всех периодов. В дальнейшем будем считать, что ожидания агентов относительно реальной ставки процента совпадают с фактической ставкой
, причем (ожидаемая) реальная ставка процента одинакова для всех периодов. В дальнейшем будем считать, что ожидания агентов относительно реальной ставки процента совпадают с фактической ставкой 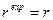 . Это предположение означает, что у населения есть основания полагать, что ожидаемая инфляция будет неизменной для рассматриваемого временного горизонта. Кроме того, будем считать, что налоги и трансферты отсутствуют. Тогда активы периода t будут равны активам предыдущего периода с поправкой на процент по этим активам плюс доход периода t за вычетом потребления в этом периоде:
. Это предположение означает, что у населения есть основания полагать, что ожидаемая инфляция будет неизменной для рассматриваемого временного горизонта. Кроме того, будем считать, что налоги и трансферты отсутствуют. Тогда активы периода t будут равны активам предыдущего периода с поправкой на процент по этим активам плюс доход периода t за вычетом потребления в этом периоде: .
.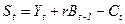 .
. , которые могут быть положительны (в этом случае потребитель действительно сберегает) и отрицательны (в этом случае потребитель является заемщиком).
, которые могут быть положительны (в этом случае потребитель действительно сберегает) и отрицательны (в этом случае потребитель является заемщиком). ,
, .
. . Учитывая, что, по предположению, активы в конце жизни равны нулю, то сбережения второго периода равны:
. Учитывая, что, по предположению, активы в конце жизни равны нулю, то сбережения второго периода равны:  , то есть во втором периоде полностью проедаются сбережения первого периода. Из соотношений (3) и (4) с учетом того, что
, то есть во втором периоде полностью проедаются сбережения первого периода. Из соотношений (3) и (4) с учетом того, что  , получаем двухпериодное бюджетное ограничение:
, получаем двухпериодное бюджетное ограничение:
 , где
, где 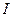 -доход в виде денег.
-доход в виде денег.
 . Если первоначальные активы присутствуют, то они также учитываются при подсчете богатства, с поправкой на накопленные проценты.
. Если первоначальные активы присутствуют, то они также учитываются при подсчете богатства, с поправкой на накопленные проценты. ,
,


