
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разделение решения об инвестициях и решения о потреблении (теорема отделимости)Содержание книги
Поиск на нашем сайте
Рассмотрим двухпериодную модель для домохозяйства, как мы это делали при выборе решения о потреблении, однако введем дополнительные возможности для перераспределения ресурсов между периодами. Предположим, что часть ресурсов (I1) в первом периоде можно направить на инвестиции, которые позволят увеличить выпуск во втором периоде на величину F(K), где F(K) -производственная функция и K=K0+I1. Считая, что капитал полностью изнашивается за один период, получаем следующее бюджетное ограничение: (1) Задача потребителя заключается в оптимальном выборе потребления в каждом периоде и объема инвестиций, то есть потребитель максимизирует функцию полезности при ограничении (1): (2) Будем считать, что первоначальный запас капитала равен нулю Как видно из рисунка 1, решение о производстве непосредственно отразится на бюджетном множестве потребителя: изменяя наше решение об инвестициях мы можем расширить бюджетное множество. Так, перейдя из исходной точки А в Е мы добились сдвига бюджетного ограничения вправо-ввверх, что увеличило количество доступных потребителю наборов. Однако данный уровень инвестиций не является наилучшим, поскольку мы могли бы немного уменьшив инвестиции, перейти в точку В, что позволило бы нам включить в бюджетное множество целую область ранее не доступных потребителю наборов. Заметим, что сдвинувшись из точки В влево или вправо мы лишь потеряем ряд потребительских наборов, но ничего не приобретем взамен, таким образом точка В дает максимально большое бюджетное множество. Таким образом, выбрав уровень инвестиций, соответствующий точке В, мы получим все возможные потребительские наборы, которые были бы доступны потребителю при любых других инвестиционных решениях. Это означает, что в данном множестве заведомо содержится оптмимальный набор каковы бы ни были предпочтения данного потребителя. Итак, как мы показали, решение о производстве не зависит от вида кривых безразличия, поскольку главная задача при выборе уровня инвестиционных расходов заключается в том, чтобы максимально расширить бюджетное множество потребителя. Для этого индивидууму следует выбрать максимальный уровень богатства (W), которое в данном случае может быть представлено следующим образом:
Рис. 1. Разделение решений о производстве и потреблении в двухпериодной модели.
Для максимизации богатства необходимо найти такую точку на границе множества производственных возможностей, в которой наклон равен -(1+r). Действительно из условия первого порядка для задачи (2) имеем: (3) В результате получаем, что производить нужно в точке В, а оптимальное потребление будет в точке D. Итак, задача домохозяйства разбивается на две самостоятельные задачи. На первом шаге осуществляется выбор оптимального уровня инвестиций путем решения задачи максимизации богатства, а на втором шаге решается стандартная задача выбора оптимального потребления при заданном уровне богатства. Заметим, что подобное разбиение возможно только при условии совершенства финансового рынка, то есть, требуется совпадение ставок процента по кредитам и депозитам. Этот результат имеет важное значение, поскольку позволяет делегировать решение о выборе инвестиций другому агенту (например, менеджеру), поставив перед ним задачу максимизации богатства, при этом разница в предпочтениях этих агентов не оказывает влияния на оптимальность принимаемого решения. Полученный нами вывод о возможности разделения решения о потреблении и решения о производстве носит название теоремы отделимости.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.184 (0.006 с.) |

 .
.
 и изобразим решение задачи (2) графически (смотри рис.1). Первоначальный запас потребителя представлен на рисунке точкой A. Если бы не было возможностей для инвестирования, то потребитель выбирал бы оптимальное потребление на бюджетной линии, проходящей через точку А с наклоном, равным –(1+r), где r- реальная ставка процента. Возможность инвестирования позволяет потребителю расширить бюджетное множество. Эти возможности отражены на рисунке с помощью производственной функции F(K), которая наложена на рисунок в зеркальном отражении с началом координат в точке А. Таким образом, путем инвестирования потребитель может изменить доставшийся ему первоначальный запас, сдвинувшись вдоль кривой, отражающей производственные возможности, в любую точку левее точки А, например, в точку Е. В силу того, что ставка процента по кредитам совпадает со ставкой процента по депозитам, наклон бюджетного ограничения будет одинаков слева и справа от точки производства Соответственно в этом случае бюджетное ограничение потребителя будет представлено прямой с наклоном –(1+r), проходящей через выбранную точку (например, Е).
и изобразим решение задачи (2) графически (смотри рис.1). Первоначальный запас потребителя представлен на рисунке точкой A. Если бы не было возможностей для инвестирования, то потребитель выбирал бы оптимальное потребление на бюджетной линии, проходящей через точку А с наклоном, равным –(1+r), где r- реальная ставка процента. Возможность инвестирования позволяет потребителю расширить бюджетное множество. Эти возможности отражены на рисунке с помощью производственной функции F(K), которая наложена на рисунок в зеркальном отражении с началом координат в точке А. Таким образом, путем инвестирования потребитель может изменить доставшийся ему первоначальный запас, сдвинувшись вдоль кривой, отражающей производственные возможности, в любую точку левее точки А, например, в точку Е. В силу того, что ставка процента по кредитам совпадает со ставкой процента по депозитам, наклон бюджетного ограничения будет одинаков слева и справа от точки производства Соответственно в этом случае бюджетное ограничение потребителя будет представлено прямой с наклоном –(1+r), проходящей через выбранную точку (например, Е). .
.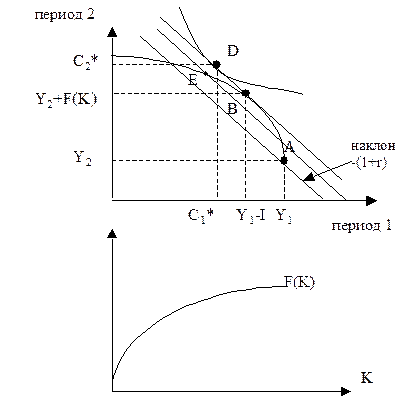
 или
или  .
.


