
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неинерциальные системы отсчетаСодержание книги
Поиск на нашем сайте
ЛЕКЦИЯ № 13 Что такое силы инерции. Силы инерции при поступательном движении. Центробежная сила инерции. Сила Кориолиса Что такое силы инерции Законы Ньютона справедливы только в инерциальных системах отсчета (см. лекцию 4, § 2). Неинерциальными являются системы отсчета, которые движутся ускоренно относительно неинерциальных. Например, система отсче- та, связанная с Землей, является неинерциальной из-за вращения нашей плане- ты вокруг собственной оси и поступательного движения по эллипсу вокруг Солнца. Правда, этой неинерциальностью в первом приближении можно пре- небречь, но при более точных расчетах ее необходимо учитывать. Учет этот можно сделать, если проводить расчеты в инерциальной системе отсчета (на- пример, связанной с Солнцем – гелиоцентрической), либо добавить во второй закон Ньютона так называемые силы инерции и рассчитать движение тела в неинерциальной системе отсчета. Силы инерции не являются силами взаимодействия рассматриваемого те- ла с какими-либо другими телами, а добавляются во второй закон Ньютона для учета ускоренного движения неинерциальной системы отсчета. Поэтому их, в отличие от истинных сил, называют фиктивными силами. Поэтому понятно, что силы инерции не подчиняются третьему закону Ньютона. Обозначим через a, как и в предыдущих лекциях, ускорение материальной
w a a откуда .
(13.1)
ma ma
(13.2)
По второму закону Ньютона (4.4), произведение ma сумме всех истинных сил, действующих на тело, т.е.:
равно F – векторной
тогда из (13.2) получим: ma F,
F ma mw. (13.3) Выразим из (13.3) произведение массы материальной точки на ее ускоре- ' ние a в неинерциальной системе отсчета:
Введем величину:
(13.4)
(13.5)
и назовем ее суммой сил инерции. Как видно, сумма сил инерции просто равна по величине и противоположна по направлению произведению массы тела на w – разность ускорений материальной точки по отношению к инерциальной и неинерциальной системам отсчета. С учетом (13.5) выражение (13.4) будет иметь вид второго закона Ньютона, записанного в неинерциальной системе отсчета:
ma F F.
(13.6)
В отличие от второго закона Ньютона (4.4), в правую часть которого вхо- дят только истинные силы (т.е. силы, подчиняющиеся третьему закону Ньюто- на), в правой части выражения (13.6) находятся и фиктивные силы, или силы инерции.
§ 2. Силы инерции при поступательном движении системы отсчета
этом случае действующие на материальную точку силы инерции F Fин , в соответствии с (13.5), также будут одинаковыми в любом месте не-
F (13.7)
Отметим, что если неинерциальная система отсчета движется поступа- тельно, но по криволинейной траектории, то ее ускорение можно разложить на две составляющие: нормальное wn и тангенциальное w (см. лекцию 3, § 1).
Fин
Рассмотрим пример, когда неинерциальная система отсчета Из рис. 13.1 очевидно, что:
y . (13.9) z
Рис. 13.1 Продифференцировав равенства (13.9) дважды по времени, получим:
d 2z
dt 2 d 2z
или, по (2.9а):
w x,
Последнее равенство можно переписать в векторном виде:
(13.10)
Пусть, например, материальная точка покоится в системе К, тогда ее ко- ординаты x, y, z постоянны, значит, ее ускорение в системе К:
Тогда из (13.10) следует, что в этом случае:
a
т.е. для наблюдателя в системе
нию самой системы К. Скажем, Вы сидите в троллейбусе и смотрите из окна на лежащий на земле камень. Троллейбус трогается от остановки с ускорением
правленным противоположно ускорению троллейбуса w. Желая применить второй закон Ньютона в системе, связанной с троллейбусом, Вы запишите
a
ной силы:
Теперь разберем другой пример с тем же троллейбусом. Пусть Вы стоите в пустом проходе троллейбуса, троллейбус трогается от остановки и начинает двигаться с ускорением
w. Вы чувствуете, что на Вас действует сила Mw, направленная в сторону, противоположную ускорению троллейбу- са. И, хотя эта сила фиктивная и не подчиняется третьему закону Ньютона (нельзя указать тело, являющееся источником этой силы!), под действием этой силы верхняя часть Вашего тела приобретет ускорение
(ноги удерживает сила трения!), и Вы вполне реально начинаете падать (относительно троллейбу- са). С точки зрения Вашего друга, наблюдавшего эту же ситуацию с остановки (в инерциальной системе К), на Вашу голову не действуют никакие силы, и она, по первому закону Ньютона, остается в покое относительно системы К (ос- тановки). А вот троллейбус уезжает от Вас вперед с ускорением. Ноги за счет силы трения приобретают ускорение падать! w, а голова пока в покое, и Вы начинаете
§ 3. Центробежная сила инерции
Рис. 13.2
Материальная точка (Ваше тело) в системе К движется по окружности ра- диусом R с ускорением a, направленным к центру этой окружности. Это уско- рение определяется, в соответствии формулой (7.7):
a . (13.11)
Вектор R на рис. 13.2 направлен от центра окружности к материальной точке, ускорение a направлено против вектора R. В инерциальной системе К, связанной с землей, причиной ускорения явля- ется сила F, с которой Вы тянете или толкаете себя, держась за какую-либо часть троллейбуса, к центру окружности. (Если Вам повезло и Вы сидите, то на Вас такая же сила действует со стороны кресла троллейбуса.) По второму закону Ньютона, в инерциальной системе К:
ma F. С учетом (13.11) отсюда имеем:
F. (13.12)
Желая применить второй закон Ньютона в этой системе отсчета, Вы, чтобы по-
должны записать:
ma
т.е. в системе В уравнении (13.13) F – реальная сила,
Fц.б. имеем:
Fц.б. mω2R . (13.14)
Эту силу инерции называют центробежной силой инерции, так как она на- правлена от центра окружности (по вектору R, как следует из формулы (13.14) и из личного опыта каждого пассажира). Центробежная сила инерции не зависит от того, покоится ли тело в систе- ме входит в формулу (13.14)). При точных расчетах поведения тел в системе от- счета, связанной с Землей, нужно учитывать центробежную силу инерции. Эта сила максимальна на экваторе, где R = Rз = 6,38 Тз = 60
6,28
7,27 10 рад.
z действует, в соответствии с (13.14), центробежная сила инерции:
5 2 6,38 106
является равнодействующей гравитационной силы Fγ, направленной к центру Земли и центробежной силы инерции Fц.б., направленной перпендикулярно оси вращения Земли. В результате этого направление силы тяжести mg не сов- падает с направлением к центру Земли (за исключением экватора и полюсов). Величина ускорения свободного падения зависит от широты: на экваторе ми- нимальна гравитационная сила (из-за сплюснутости Земли с полюсов) и макси- мальна центробежная, в результате там значение g минимально и равно gэкв = 9,780 м/с2. На полюсах g максимально и равно gпол = 9,832 м/с2. § 4. Сила Кориолиса При движении тела во вращающейся системе отсчета, кроме центробеж- ной силы инерции, возникает еще одна, которую называют силой Кориолиса, или кориолисовой силой. Величина этой силы определяется формулой:
здесь m – масса тела; к 2m v ω, (13.15) v ω – вектор угловой скорости вращения неинерциальной системы отсчета.
Тогда относительно системы
v ωR . (13.16)
Рис. 13.3
Fц.б. mω2R.
Но для движения по окружности необходима сила, направленная к центру этой окружности. Значит, кроме центробежной силы инерции, на наше тело должна в системе
a aц.с. Rω2
. (13.17)
Кориолиса Fк. Действительно, в соответствии с (13.15), Fк направлена (в соот- ветствии с правилом правого винта) к центру окружности. Ее модуль, с учетом
Fк 2mω R.
Fц.б. 2mω2R mω2R mω2R.
F -mω2R. (13.18) Если мы желаем применить второй закон Ньютона в неинерциальной сис- теме отсчета, то мы должны сумму всех сил, включая и фиктивные, приравнять
0, тогда:
ma . 13.19) Подставляя (13.17) и (13.18) в (13.19), видим, что
Вывод формулы (13.15) достаточно сложен, и мы его не приводим. Разо- бранный пример прост и убедительно показывает правильность формулы (13.15). Сила Кориолиса играет исключительно важную роль при движении боль- ших потоков океанических вод и атмосферного воздуха на нашей планете. Силу Кориолиса должны учитывать артиллеристы и ракетчики при стрельбе на даль- ние расстояния. Эта же сила приводит к тому, что у рек в северном полушарии подмывается всегда правый берег (например, крутые правые берега у Оби), в южном – левый.
ИТОГИ ЛЕКЦИИ № 13 1. Для использования второго закона Ньютона в неинерциальных системах отсчета надо, кроме истинных сил, учитывать фиктивные силы или силы инер- ции. 2. Силы инерции не являются силами взаимодействия, поэтому не подчи- няются третьему закону Ньютона. 3. Суммарная сила инерции
mw, где w определяется в соответствии с (13.1):
4. При поступательном движении неинерциальной системы отсчета отно-
сительно инерциальной силы инерции F
одинаковы в любом месте не- инерциальной системы и не зависят от скорости движения частицы, их величи- на определяется формулой (13.7): Fин
где w – ускорение неинерциальной системы отсчета относительно инерциаль- ной. 5. Во вращающейся системе отсчета действуют центробежные силы инер- ции и силы Кориолиса. 6. Fц.б. не зависит от скорости час- Fц.б. mω2R,
R – расстояние от материально точки массой m до оси вращения. 7. действует на частицу массой m, движущуюся со скоростью скоростью ω (см. (13.15)):
Направление силы Кориолиса перпендикулярно векторам
Учебное издание Тюшев Александр Николаевич Вылегжанина Вера Дмитриевна
КУРС ЛЕКЦИЙ ПО ФИЗИКЕ
Часть 1 Механика Пособие для студентов 1 и 2 курсов
Ответственный редактор: Серегин Г.В. Редакторы: Деханова Е.К. Шилова Л.Н.
Подписано в печать 30.04.03. Формат 60 84 1/16 Печать цифровая Усл. печ. л. 6.68. Уч.-изд. л. 6.85. Тираж 100 Заказ Цена договорная
Гигиеническое заключение № 54.НК.05.953.П.000147.12.02. от 10.12.2002.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.013 с.) |





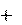
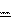

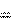 '
' 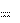
 '
' mw.
mw.

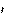 Напомним, что поступательным называется такое движение, при котором любая линия, проведенная в теле, остается при его движении параллельной са- мой себе. Применительно к движущейся неинерциальной системе отсчета К это означает, что оси ее системы координат сохраняют при движении свое на- правление относительно осей координат инерциальной системы отсчета К. Иными словами, ускорение w, входящее в формулу (13.1), является величи- ной, не зависящей от положения материальной точки, и представляет собой ус- корение неинерциальной системы отсчета относительно инерциальной.
Напомним, что поступательным называется такое движение, при котором любая линия, проведенная в теле, остается при его движении параллельной са- мой себе. Применительно к движущейся неинерциальной системе отсчета К это означает, что оси ее системы координат сохраняют при движении свое на- правление относительно осей координат инерциальной системы отсчета К. Иными словами, ускорение w, входящее в формулу (13.1), является величи- ной, не зависящей от положения материальной точки, и представляет собой ус- корение неинерциальной системы отсчета относительно инерциальной. ' В
' В инерциальной системы отчета и не будут зависеть от скорости частицы:
инерциальной системы отчета и не будут зависеть от скорости частицы: Соответственно этому можно ввести две составляющие силы инерции:
Соответственно этому можно ввести две составляющие силы инерции:
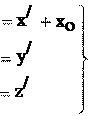 x
x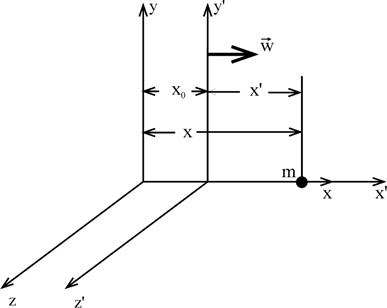
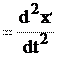
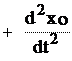 d 2 x
d 2 x dt 2 ,
dt 2 ,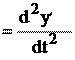 d 2 y
d 2 y dt 2 ,
dt 2 ,
 dt 2
dt 2 a x a x
a x a x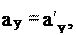
 .
.
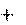
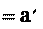 a w.
a w.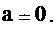
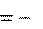
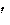 w,
w, жется с ускорением a, направленным в сторону, противоположную ускоре-
жется с ускорением a, направленным в сторону, противоположную ускоре-


 F mw.
F mw. F
F 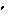

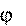
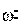 Оси x и y неподвижны относительно земли, а оси
Оси x и y неподвижны относительно земли, а оси 
 ω t.
ω t.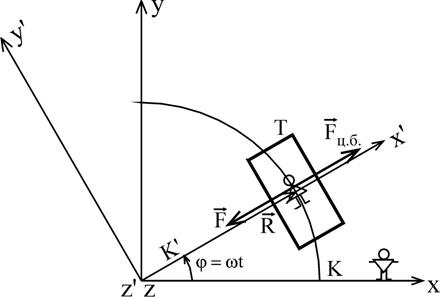

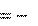
 В неинерциальной системе
В неинерциальной системе  Вы покоитесь, Ваше ускорение
Вы покоитесь, Ваше ускорение 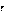 0.
0.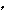 лучить нулевое ускорение a,
лучить нулевое ускорение a,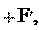
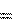
 так как a 0, то предыдущее уравнение переходит в следующее:
так как a 0, то предыдущее уравнение переходит в следующее: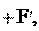
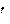 – сила инерции. С учетом
– сила инерции. С учетом (13.12) из (13.13) для силы инерции F
(13.12) из (13.13) для силы инерции F
 (скорость не
(скорость не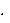 106 м. Угловая скорость вра- щения Земли вокруг своей оси может быть найдена по формуле (7.9), куда в ка- честве периода Тз надо подставить количество секунд в сутках:
106 м. Угловая скорость вра- щения Земли вокруг своей оси может быть найдена по формуле (7.9), куда в ка- честве периода Тз надо подставить количество секунд в сутках: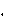
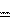 С учетом этого имеем:
С учетом этого имеем: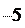 c
c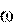 На тело массой m = 1 кг на экваторе с учетом приведенных значений Rz и
На тело массой m = 1 кг на экваторе с учетом приведенных значений Rz и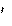 F ц.б.
F ц.б.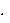
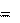
 1 7,27 10
1 7,27 10 что составляет 1/291 часть от силы тяжести, равной 9,81 Н. Сила тяжести mg
что составляет 1/291 часть от силы тяжести, равной 9,81 Н. Сила тяжести mg

 F
F  – вектор скорости тела относительно вращающейся (неинерциальной) системы отсчета;
– вектор скорости тела относительно вращающейся (неинерциальной) системы отсчета;


 Эта ситуация изображена на рис. 13.3. Как мы знаем из предыдущего пара- графа, на тело массой m во вращающейся системе отсчета К, независимо от состояния его движени,я действует центробежная сила инерции, направленная, в соответствии с формулой (13.14), от центра окружности, по которой движет- ся тело:
Эта ситуация изображена на рис. 13.3. Как мы знаем из предыдущего пара- графа, на тело массой m во вращающейся системе отсчета К, независимо от состояния его движени,я действует центробежная сила инерции, направленная, в соответствии с формулой (13.14), от центра окружности, по которой движет- ся тело:
 Этой второй фиктивной силой в нашей системе отсчета и является сила
Этой второй фиктивной силой в нашей системе отсчета и является сила (13.16) и (13.15), равен: 2
(13.16) и (13.15), равен: 2

 F Fк
F Fк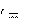 В векторном виде:
В векторном виде: к массе тела, умноженной на его ускорение a aц.c.. Так как тело покоилось в
к массе тела, умноженной на его ускорение a aц.c.. Так как тело покоилось в системе К, то сумма реальных сил F
системе К, то сумма реальных сил F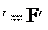
 - векторная сумма си- лы Кориолиса и центробежной силы сообщают телу центростремительное ус- корение. Действительно:
- векторная сумма си- лы Кориолиса и центробежной силы сообщают телу центростремительное ус- корение. Действительно: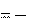
 mRω2 mω2R.
mRω2 mω2R.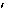 , действующая на тело массой m в неинер- циальной системе отсчета, равна по величине и противоположна по направле- нию произведению массы тела на w разность ускорений материальной точки по отношению к инерциальной и неинерциальной системам отсчета, т.е. п (13.5):
, действующая на тело массой m в неинер- циальной системе отсчета, равна по величине и противоположна по направле- нию произведению массы тела на w разность ускорений материальной точки по отношению к инерциальной и неинерциальной системам отсчета, т.е. п (13.5):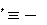

 w a
w a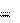 Fин
Fин mw,
mw,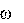 где - угловая скорость вращения неинерциальной системы отсчета относи- тельно инерциальной;
где - угловая скорость вращения неинерциальной системы отсчета относи- тельно инерциальной; Сила Кориолиса F к
Сила Кориолиса F к относительно неинерциальной системы отсчета, вращающейся со
относительно неинерциальной системы отсчета, вращающейся со


 F к 2m v / ω.
F к 2m v / ω.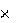 Изд. лиц. № ЛР 020461 от 04.03.1997.
Изд. лиц. № ЛР 020461 от 04.03.1997.


