
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость. Вычисление пройденного пути. Ускорение
§1. Скорость Слово «скорость» мы часто используем в своей речи и на обыденном уровне представляем себе, что оно означает величину, характеризующую либо быстроту движения, либо быстроту какого-либо процесса. Однако, для того, чтобы ввести в механику точный физический термин «скорость», потребовалось создать новую область математики – научиться опе- рировать с бесконечно малыми величинами. Известны многочисленные пара- доксы, связанные с проблемой скорости движения. Вот один из них, принадле- жащий древнегреческому философу Зенону Элейскому, жившему примерно 2 500 лет тому назад. В этом парадоксе утверждается, что быстроногий Ахил- лес никогда не сможет догнать медлительную черепаху. Вот как излагает рас- суждения Зенона известный американский физик Ричард Фейнман в первом томе своих лекций по физике. Предположим, что Ахиллес бегает в десять раз быстрее черепахи. Пусть в начале состязания черепаха находилась в 100 метрах впереди Ахиллеса. Тогда ко времени, когда Ахиллес пробежит эти 100 метров, черепаха окажется в 10 метрах впереди него. Пробежав и эти 10 метров, Ахил- лес увидит черепаху в 1 метре впереди себя. За то время, пока он пробежит этот метр, черепаха пройдет 10 сантиметров и так далее… до бесконечности. Следо- вательно, в любой момент времени черепаха будет впереди Ахиллеса, и он ни- когда не сможет перегнать ее! В чем ошибочность этих рассуждений? Конеч- ный интервал времени можно разделить на бесконечное число частей. Но бес- конечное число этапов до того места, где Ахиллес поравняется с черепахой, вовсе не означает бесконечное количество времени. Для того, чтобы научиться правильно оперировать с бесконечно малыми величинами, человечеству пона- добилось примерно 2 000 лет. Честь создания дифференциального и интеграль- ного исчисления принадлежит И. Ньютону (наряду с Г. Лейбницем). В своем грандиозном труде «Математические начала натуральной философии» (1687 г.) Ньютон сформулировал исходные понятия и основные законы классической механики.
Сейчас мы дадим точное и строгое определение физического термина «скорость». Исходя из этого определения, выясним свойства скорости. Скорость – это производная радиус-вектора по времени.
Как видно из этого определения, скорость – величина векторная, т.е. когда употребляют термин «скорость», имеют в виду вектор, который имеет две ха- рактеристики: направление и модуль.
Скорость направлена по касательной к траектории. Это можно устано- вить, проанализировав определение скорости (2.1). Так как
На рис. 2.1а, 2.1б, 2.1в показаны этапы предельного перехода для плоского движения, когда материальная точка движется по произвольной траектории.
r2 r1 этой материальной точки за промежуток времени t t2 t1. Отношение перемещения к
дает среднюю скорость <v> материальной точки за
v (2.1б)
падает с направлением вектора перемещения.
r2 приближается к r1. При этом вектор перемещения меняет свое направление, он поворачи-
жуточное положение при совершении предельного перехода ( t 0) зафикси- ровано на рис. 2.1б.
При дальнейшем уменьшении и приближении r2 к r1 направление век-
из геометрии, касательная есть предельное положение секущей.
перемещения будет направлен по касательной к траектории.
Следовательно, и вектор скорости будет направлен по касательной к траектории. Это изображено на рис. 2.1в.
Рис. 2.1а
Рис. 2.1б
Рис. 2.1в Компоненты скорости На рис. 2.2 изображен вектор скорости v материальной точки, движущей- ся по плоскости x, y. Вектор v можно разложить на два составляющих его век-
тора ex vx и eyvy .
Рис. 2.2 Компоненты скорости, т.е. проекции вектора v на координатные оси обо- значены vx, vy. Так как на рис. 2.2 вектор ex vx направлен по оси х, то компо- нента скорости vx > 0. Вектор ey v y у нас направлен против оси, значит, соот- ветствующая компонента скорости vy < 0. Из определения (2.1) и формулы (1.1) следует, что для трехмерного про- странства скорость в декартовых координатах выражается следующим обра- зом:
(2.1а)
v ex vx ey vy ez vz , (2.1б)
и vz , (2.2)
т.е. компоненты скорости в декартовых координатах равны производным со- ответствующих координат по времени.
скорости из определения (2.1а):
v (2.3)
Выразим модуль скорости через ее компоненты. По теореме Пифагора (см. рис. 2.2):
В трехмерном пространстве v
.
и модуль скорости:
(2.4)
§2. Вычисление пройденного пути Для равномерного движения, т.е. для движения с постоянной по модулю
v const, путь равен: s12
vt , (2.5) где s12 – весь путь (рис. 2.3); t – весь отрезок времени;
Рис. 2.3 Формула (2.5), известная по школьному курсу физики, следует из формулы (2.3). Запишем формулу (2.3) в следующем виде:
тогда v ds,
здесь ds – бесконечно малый отрезок пути, пройденный за бесконечно малое время dt. Складывая все ds, получим s12, сумма всех dt даст время движения t. Опе- рация сложения бесконечно малых величин носит в математике название ин- тегрирования. Интегрируя (2.3а), получим:
vdt 1 0 t v 0 В правой части мы вынесли за знак интеграла скорость v, так как она в на- шем случае постоянна. Интеграл от ds есть s12, а интеграл от dt – время движе- ния t, следовательно, мы получим формулу, совпадающую с (2.5):
vt.
sn v1 t1
v2 t2 ... vi ti ... vn tn.
Рис. 2.4
в течение отрезка времени
тельно постоянны, если В пределе: достаточно малы.
s12 n
t 0 i 1 t2
t1
т.е. путь – это определенный интеграл от модуля скорости по времени. Так как модуль скорости – величина положительная, то путь всегда поло- жителен и может только возрастать с течением времени.
§3. Ускорение В общем случае скорость материальной точки может изменяться как по величине (т.е. по модулю), так и по направлению. Быстроту этого изменения характеризует векторная величина, которую называют термином «ускорение».
Ускорение – это производная скорости по времени. Учитывая, что v или .
(2.7)
d2
. (2.8) a dt dt dt2
Вектор ускорения a, так же, как и векторы r
и v, можно разложить на
eya y ezaz,
где ах, аy, аz – компоненты ускорения.
, ay y , a
Используя формулы (2.8) и (1.1), получим, что:
, az
т.е. компоненты ускорения равны вторым производным по времени от соот- ветствующих координат материальной точки. §4. Нахождение зависимости скорости от времени Запишем первую из формул (2.7) в следующем виде:
Формула (2.7а) позволяет найти приращение скорости dv за бесконечно малый промежуток времени dt. Если известна начальная скорость
0 ), то, используя (2.7а), можно найти скорость спустя бесконечно
(2.10)
Если нам известна зависимость ускорения от времени, т.е. функция A(t), то начатый формулой (2.10) процесс вычисления зависимости v ( t ) - скорости от времени – можно бесконечно продолжать. В математике эта операция назы- вается интегрированием. Возьмем определенный интеграл в пределах от нуля до t от обеих частей равенства (2.7а):
dv vo t
0
(2.11)
Как известно из математики, интеграл от дифференциала dv равен разно- сти значений функции v на верхнем и нижнем пределах. Тогда из (2.11) полу- чим:
откуда для
V(t)
имеем:
t
0
v(t) v0 t
0
(2.12) Для нахождения зависимости v ( t ) по формуле (2.12) необходимо в каждом конкретном случае взять интеграл от ускорения по времени.
ИТОГИ ЛЕКЦИИ № 2 1. Скорость – производная радиус-вектора по времени (2.1):
v dt Направлена скорость по касательной к траектории. 2. Компоненты скорости равны производным соответствующих коорди- нат по времени (2.2):
3. Модуль скорости – производная пути s по времени (2.3):
. dt 4. Модуль скорости связан с ее компонентами следующим образом (2.4):
5. При равномерном движении, т.е. при v Const,
пройденный путь s12
6. Для произвольного движения путь равен определенному интегралу от модуля скорости по времени (2.6)
s12 = lim viΔti = v(t)dt.
7. Ускорение – это производная скорости по времени (2.7):
a dt 8. Ускорение – это вторая производная радиус-вектора по времени (2.8):
a . dt
9. Компоненты ускорения ах, аy, аz равны производным по времени от со- ответствующих компонент скорости (2.9):
и вторым производным по времени от соответствующих координат (2.9а):
10. Зависимость скорости материальной точки от времени может быть найдена (2.11), если известно ускорение как функция времени:
v ( t ) v0 t
0 ЛЕКЦИЯ № 3
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.253.221 (0.164 с.) |
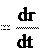
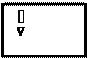 либо, применяя другое обозначение производной по времени,
либо, применяя другое обозначение производной по времени, . (2.1)
. (2.1)
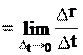
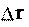 то направление вектора v совпадает с предельным направлением вектора.
то направление вектора v совпадает с предельным направлением вектора. На рис. 2.1а изображены радиус-векторы материальной точки для момен-
На рис. 2.1а изображены радиус-векторы материальной точки для момен-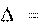


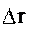 тов времени t1 и t2, а также вектор перемещения r
тов времени t1 и t2, а также вектор перемещения r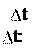 промежутку времени промежуток времени
промежутку времени промежуток времени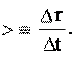

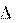
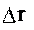 При уменьшении промежутка времени t радиус-вектор
При уменьшении промежутка времени t радиус-вектор вается против часовой стрелки. Модуль вектора уменьшается. Это проме-
вается против часовой стрелки. Модуль вектора уменьшается. Это проме-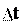
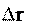 тора приближается к направлению касательной к траектории. Как известно
тора приближается к направлению касательной к траектории. Как известно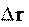 Значит, когда предельный переход будет завершен, бесконечно малый вектор
Значит, когда предельный переход будет завершен, бесконечно малый вектор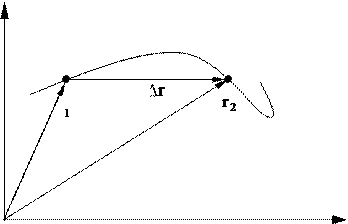 y
y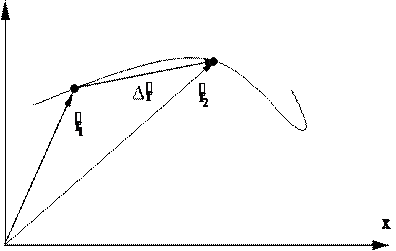 y
y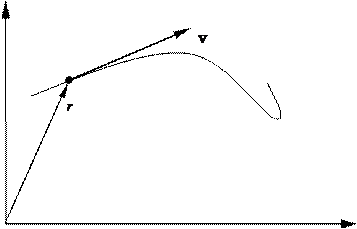 y
y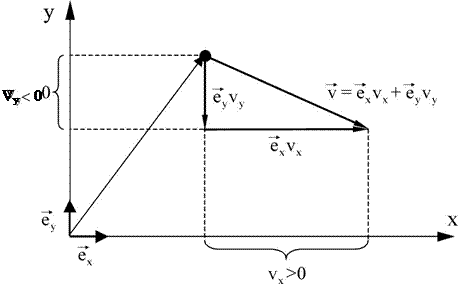
 С другой стороны:
С другой стороны:
 v r ex x
v r ex x
 ey y
ey y ez z
ez z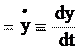
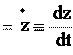 откуда
откуда vx , vy
vx , vy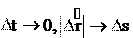 Модуль скорости – это производная пути по времени. В самом деле, при (см. рис. 1.8, 2.1а, 2.1б). Используя это, получим для модуля
Модуль скорости – это производная пути по времени. В самом деле, при (см. рис. 1.8, 2.1а, 2.1б). Используя это, получим для модуля

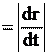
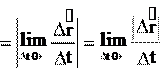
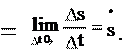





 ex vx
ex vx
 ey vy
ey vy


 скоростью: v
скоростью: v

 dt
dt ds vdt, (2.3а)
ds vdt, (2.3а)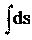
 2 t
2 t dt.
dt. s12
s12
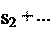 Для произвольного движения (рис. 2.4), т.е. для движения с переменной скоростью разобьем весь путь на очень маленькие участки
Для произвольного движения (рис. 2.4), т.е. для движения с переменной скоростью разобьем весь путь на очень маленькие участки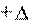
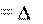 s12 s1
s12 s1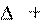
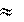
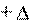
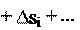
 v1
v1
 Значения модуля скорости vi
Значения модуля скорости vi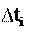 приблизи-
приблизи-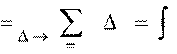 v(t)dt, (2.6)
v(t)dt, (2.6)


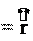 Ускорение – вторая производная радиус-вектора по времени. Производ- ную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение – это скорость изменения скорости.
Ускорение – вторая производная радиус-вектора по времени. Производ- ную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение – это скорость изменения скорости.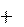
 a exax
a exax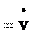 Из определения (2.7) и формулы (2.1б) следует, что:
Из определения (2.7) и формулы (2.1б) следует, что:
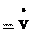 ax x
ax x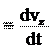
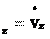 , (2.9)
, (2.9) т.е. компоненты ускорения равны производным по времени от соответствую- щих компонент скорости.
т.е. компоненты ускорения равны производным по времени от соответствую- щих компонент скорости.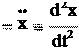
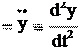 ax , ay
ax , ay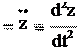 , (2.9а)
, (2.9а)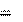 dv a ( t ) dt. (2.7а)
dv a ( t ) dt. (2.7а)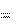 малый интервал dt:
малый интервал dt: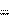 v t dt
v t dt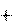
 v0 a(t)dt.
v0 a(t)dt. v(t)
v(t)  a(t)dt.
a(t)dt. v(t) v0
v(t) v0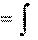 a(t)dt,
a(t)dt,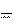
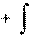 a(t)dt.
a(t)dt.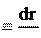



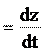 vx , vy , vz .
vx , vy , vz .
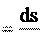
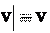

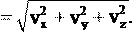
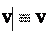

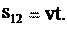
 n t2
n t2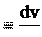
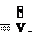
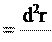
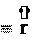
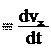
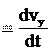
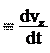
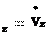
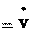
 ax x , ay y , a
ax x , ay y , a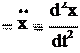

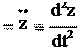 ax , ay , az .
ax , ay , az .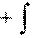 a ( t ) dt.
a ( t ) dt.


