
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия. Закон сохранения полной механической энергииСодержание книги
Поиск на нашем сайте
§ 1. Консервативные и неконсервативные силы Консервативные (от латинского conservativus – охранительный) – это та- кие силы, РАБОТА которых не зависит от траектории, а определяется только начальным и конечным положением материальной точки. Силы, не обладающие только что названным свойством, называют некон- сервативными. Для того чтобы узнать, консервативна сила либо нет, надо вычислить ее работу.
Консервативность силы тяжести
Рис. 6.1 Вычислим работу (5.4) силы тяжести mg
(4.7) при движении материаль- ной точки массой m из положения 1 в положение 2 по произвольной траекто- рии, изображенной на рис. 6.1 стрелочками. На рисунке дан вид сбоку. При вы- числении работы по формуле (5.4) воспользуемся тем, что сила тяжести
Это позволяет вынести ее за знак интеграла. Оставшийся интеграл от вектора ds дает, очевидно (рис. 6.1), вектор s12. Затем, расписав скалярное произведение gS12 = gs12 cos , выразим s12 cos через разность высот h1 h2.
2 2 A12 Fds
mgds 1 mg ds=
mgs12 mgs 12сosα mg h1 h 2
mgh 1 mgh 2. (6.1)
Неконсервативность силы трения Вычислим теперь работу (5.4) силы трения (4.9) при движении материаль- ной точки m из положения 1 в положение 2 по произвольной траектории, изо- браженной на рис. 6.2. На этом рисунке изображен вид сверху.
трения Fтр и ds всегда будет равен минус единице.
ds Fтр Известно, что пройденный путь. s12 ds – 1
Cos -1 Модуль силы трения по- стоянен. Это позволяет вынести Fтр за знак интеграла. Теперь 1 Рис. 6.2 под интегралом, в отличие от 2 предыдущего случая (вывод формулы (6.1)), остается ска- лярная величина ds. Интеграл от скаляра ds дает путь s12, который, очевидно, зависит от траектории. Реализуем эту программу:
A12 Fтр ds 1 Fтр ds сos 1 Fтр ds 1 Fтр ds 1 Fтр s12.
Ответ зависит от выбора траектории, значит, сила трения неконсерва- тивна. § 2. Потенциальная энергия Потенциальная энергия может быть введена только для поля консерва- тивных сил. Так как их работа не зависит от траектории, а зависит только от начально- го и конечного положений материальной точки, то эту работу можно записать в виде разности двух чисел: одно – WП1 – будет зависеть от начального положе- ния тела, второе – WП2 – от конечного положения тела.
где WП1 – потенциальная энергия тела в положении 1; WП2 – потенциальная энергия в положении 2. Работа в потенциальном поле сил равна убыли потенциальной энергии. Некоторые конкретные выражения для потенциальной энергии Wn(r) Для нахождения конкретного вида зависимости WП(r) необходимо вычислить
работу A12
2
1 Ds.
В частности, для однородного поля тяжести, где
Wn
mgh . (6.3)
Если F G m1m2
– гравитационная сила, то
Wn r G m1m2. r
(6.4)
Если F k q1q2
– кулоновская сила то
Wn r k q1q2
. (6.5)
kупрx – сила упругости (4.8), то
. (6.6)
§ 3. Закон сохранения механической энергии Сначала получим закон сохранения механической энергии для одной мате- риальной точки, движущейся в поле консервативных сил. Работа этих сил, с одной стороны (5.10), равна приращению кинетической энергии материальной точки: A12 = Wk2 – Wk1.
A12 Wп1 Wп2
Исключая A12 из записанных выше выражений, получим:
или Wп1
Wп2
Wk2
Wk1 ,
(6.7)
Полученное равенство означает, что в поле консервативных сил сумма ки- нетической и потенциальной энергии материальной точки остается посто- янной, т.е. сохраняется.
Сумма кинетической и потенциальной энергии материальной точки назы- вается ее полной механической энергией W:
(6.8)
Полная механическая энергия материальной точки в поле консервативных сил сохраняется. Полная механическая энергия системы материальных точек Для системы, состоящей из N взаимодействующих между собой матери- альных точек, полная механическая энергия:
W i Wп i,k Wk Wп. (6.9) 2 i, k 1 i k
Первый член в формуле (6.9) – это кинетическая энергия системы, которая равна сумме кинетических энергий материальных точек, входящих в систему. Второй член дает потенциальную энергию взаимодействия материальных точек системы между собой. В нем под знаком суммы стоит Wп i, k – потенциальная энергия взаимодействия i-й материальной точки с k-й материальной точкой. В формуле (6.9): Wk – кинетическая энергия системы; Wп – потенциальная энергия взаимодействия всех частиц системы между собой.
|
|||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.232.171 (0.008 с.) |


 mg const.
mg const.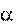
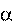
 Изложенная программа реализована следующим образом.
Изложенная программа реализована следующим образом.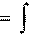
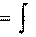 2
2 
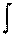 1
1
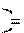
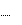

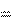 mgh1 mgh 2.
mgh1 mgh 2.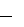 Ясно, что при любой траектории ответ будет таким же. Значит, сила тяжести консервативна, так как ее работа не зависит от выбора траектории, а определяется лишь начальным и конечным положением материальной точки:
Ясно, что при любой траектории ответ будет таким же. Значит, сила тяжести консервативна, так как ее работа не зависит от выбора траектории, а определяется лишь начальным и конечным положением материальной точки: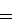 A12
A12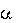 Сила трения всегда направлена против скорости, следовательно, при вы- числении работы можно воспользоваться тем, что косинус угла между силой
Сила трения всегда направлена против скорости, следовательно, при вы- числении работы можно воспользоваться тем, что косинус угла между силой 2
2 m v
m v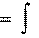
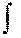
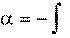
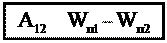
 , (6.2)
, (6.2)
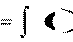 F r
F r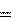 F m g, используя (6.1), получим:
F m g, используя (6.1), получим:


 r2
r2

 r
r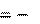 Если F
Если F
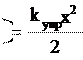 Wn x
Wn x
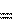 С другой стороны (6.2), та же работа равна убыли потенциальной энер- гии материальной точки:
С другой стороны (6.2), та же работа равна убыли потенциальной энер- гии материальной точки: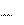 Wk1
Wk1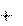 Wп1
Wп1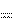
 Wk2
Wk2
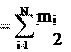
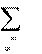 v2 1 N
v2 1 N


