
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение жидкости изображают с помощью линий тока.Содержание книги
Поиск на нашем сайте
Линии тока – это линии, касательные к ко-
Линии тока не прерываются и не пересека- ются, их густота пропорциональна скорости те- чения жидкости.
Рис 10.1 Трубка тока – это часть потока жидкости, ограниченная линиями тока (рис. 10.2). S1
V1 V2
Рис. 10.2 При стационарном течении жидкости трубка тока со временем не изменя- ется по форме, и частицы жидкости не проникают через боковую поверхность трубок. Если жидкость идеальна, то в каждой трубке тока скорость постоянна. Если жидкость несжимаема, то через два различных сечения трубки тока прой-
через сечение S1 (рис. 10.2),
S1v1 t, где v1 – скорость течения жидкости в месте сечения S1.
через сечение S2 (рис. 10.2),
S2 v 2 t, где v2 – скорость течения жидкости в месте сечения S2. Тогда: S1v1 t S2v2 t.
S2v2 const . (10.1)
Откуда следует, что v1: v2 S1: S2, т.е. скорость течения жидкости в трубе
§ 3. Уравнение Бернулли Уравнение Бернулли устанавливает зависимость между скоростью стацио- нарного течения идеальной несжимаемой жидкости и ее давлением. Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называется давлением р жидкости.
p , (10.1а)
F
– нормальная сила; – n
жидкость.
Рис 10.3 1 Па 1 Н
Выделим в стационарно текущей идеальной несжимаемой жидкости труб- ку тока. Рассмотрим стационарное течение жидкости, ограниченной трубкой тока и перпендикулярными к линиям тока сечениями S1
и S2 (рис. 10.4).
Рис 10.4 В сечении S1 В сечении S2 – давление – давление p1, высота p2, высота h1, скорость течения h 2, скорость течения v1 . v2 .
ной механической энергии незамкнутой системы равно работе внешних сил:
здесь W1 – полная механическая энергия всей рассматриваемой нами жидкости, заключенной в выделенной трубке тока между сечениями S1 и S2;
' S2, за
ных механических энергий объемов жидкости ΔV1 S1 l и ΔV2 S2 l 2 (см. рис. 10.4). Так как жидкость несжимаема, то ΔV1 ΔV2 ΔV. Масса жид- кости, заключенная в каждом из этих объемов, также одинакова и равна
Найдем работу Авнеш, совершаемую силами давления, приложенными к се-
F1 l 1 F2 l 2 p 1S1 l 1 p 2 S2 l 2 p1ΔV1 p2 ΔV2 p1 p2 ΔV . (10.3)
ления 10.1а) и, наконец, учли, что ΔV1 ΔV2 ΔV. Теперь найдем полные механические энергии W1 и W2. Для W1 имеем:
W1 1 2 Δmgh 1. (10.4) Для W2 запишем аналогичное выражение:
W2 2 2 Δmgh 2. (10.5)
Подставляя (10.4), (10.5) и (10.3) в (10.2), получим:
( 2 2 Δmgh 2) Δmv 2
2 Δmgh 1) (p1 p2)Δ V.
(10.6)
Δm/ΔV ρ – плотность
2 ρgh 2 2 2
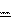
2 1
1 ρgh 2 2 2
1 2
ρgh 2
Так как сечения выбирались произвольно, то можем записать
gh p 2 const . (10.7)
Выражение (10.7) выведено швейцарским физиком и математиком Д. Бер- нулли (работал в Петербургской академии наук) и называется уравнением Бернулли. Уравнение Бернулли представляет собой выражение закона сохранения энергии применительно к стационарному течению идеальной несжимаемой жидкости.
давление, р – статическое давление. – динамическое Так как динамическое давление связано со скоростью движения жидкости, то уравнение Бернулли позволяет определить скорость потока жидкости. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Уравнение Бернулли используется, например, для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Уравнение Бернулли хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.
§ 4. Вязкость жидкости Вязкость (внутреннее трение) – это свойство реальной жидкости оказывать сопротивление движению одной части жидкости относительно другой. При пе- ремещении слоев жидкости, движущихся с разными скоростями, возникают си- лы внутреннего трения, направленные вдоль соприкасающихся слоев. Причи- ной внутреннего трения является перенос частицами жидкости импульса. В ре- зультате, более медленно движущийся слой жидкости ускоряется, а более бы- стрый слой замедляется. Сила внутреннего трения будет тем больше, чем больше площадь поверх- ности слоя S, и зависит от того, насколько быстро меняется скорость течения
v2 v1 движущиеся с неодинаковыми скоро-
стями v2 и v1 . Величина называ-
Рис. 10.5 ется градиентом скорости и показыва- ет, как быстро меняется скорость в на- правлении, перпендикулярном направ- лению движения слоев.
Модуль силы внутреннего трения равен:
Fтр η v S, (10.8)
- для воды: = 0,001 Па - для воздуха: = 0,000017 Па - для глицерина: = 0,85 Па Характер течения вязкой жидкости определяется безразмерным числом, ко- торое называется числом Рейнольдса:
– плотность жидкости; R = ρ<v>L,
(10.9) < v > – средняя скорость течения; L – линейный размер, в котором наблюдается неоднородность скорости. Например, при движении шара в жидкости таким размером является диа- метр шара, при движении жидкости в трубе – диаметр трубы и т.д. Число Рейнольдса определяет переход от ламинарного течения к турбу- лентному. Обычно турбулентное течение возникает при Rе > 103. При этом си- ла сопротивления уже не зависит от вязкости. В этом случае обмен импульсами между слоями происходит в результате активного «перемешивания» жидко- стей, а не в результате диффузии, как при ламинарном течении.
При больших Rе сопротивление сильно зависит от формы тела. Обтекае- мую форму, уменьшающую сопротивление, придают многим движущимся предметам: самолетам, автомобилям, ракетам и т.д.
ИТОГИ ЛЕКЦИИ № 10 1. При изучении движения жидкостей пользуются физическими моделями: - несжимаемая жидкость – жидкость, плотность которой всюду одинако- ва и не изменяется со временем; - идеальная жидкость – жидкость, в которой отсутствуют силы трения. 2. Движение жидкости называется течением.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.227.125 (0.009 с.) |

 v v торым совпадают по направлению с вектором скорости частиц (рис. 10.1).
v v торым совпадают по направлению с вектором скорости частиц (рис. 10.1). S2
S2
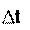 дет одинаковый объем жидкости: V1 V2 .
дет одинаковый объем жидкости: V1 V2 .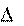
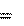 Объем жидкости, протекающий за время
Объем жидкости, протекающий за время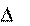 равен V1
равен V1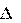
 Объем жидкости, протекающий за время
Объем жидкости, протекающий за время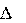 равен V2
равен V2
 Для несжимаемой жидкости уравнение неразрывности имеет вид:
Для несжимаемой жидкости уравнение неразрывности имеет вид: F n
F n 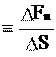
 S где
S где
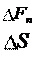 площадь пластины, помещенной в
площадь пластины, помещенной в
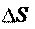 – Единица давления – паскаль.
– Единица давления – паскаль. 1 м2
1 м2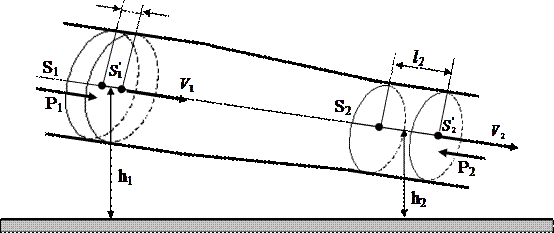 l 1
l 1 За малый промежуток времени жидкость перемещается от сечений S1 и
За малый промежуток времени жидкость перемещается от сечений S1 и W2 W1 Aвнеш, (10.2)
W2 W1 Aвнеш, (10.2) W2 – полная механическая энергия той же жидкости, но уже через проме-
W2 – полная механическая энергия той же жидкости, но уже через проме-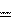
 промежуток времени t не изменится. Поэтому приращение полной механиче- ской энергии всей рассматриваемой нами жидкости будет равно разности пол-
промежуток времени t не изменится. Поэтому приращение полной механиче- ской энергии всей рассматриваемой нами жидкости будет равно разности пол-
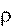 Δm ρΔV , где – плотность жидкости.
Δm ρΔV , где – плотность жидкости.

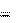
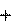
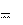 Δmv 2
Δmv 2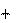
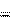 Δmv 2
Δmv 2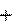 Δmv 2
Δmv 2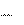 ( 1
( 1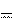
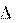 Поделив выражение (10.6) на V и учитывая, что жидкости, получим:
Поделив выражение (10.6) на V и учитывая, что жидкости, получим: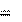
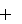
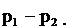
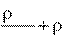
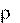
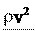 В этом уравнении: gh – гидростатическое давление, 2
В этом уравнении: gh – гидростатическое давление, 2 жидкости при переходе от слоя к слою. На рис. 10.5 условно изображены
жидкости при переходе от слоя к слою. На рис. 10.5 условно изображены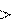 соприкасающиеся слои жидкости,
соприкасающиеся слои жидкости,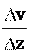
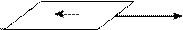 F тр
F тр
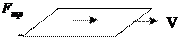


 1
1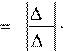 z
z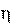 где – динамический коэффициент вязкости.
где – динамический коэффициент вязкости. Коэффициент вязкости зависит от температуры жидкости и различен для разных сред. Например, при температуре 20оС коэффициенты динамической вязкости равны:
Коэффициент вязкости зависит от температуры жидкости и различен для разных сред. Например, при температуре 20оС коэффициенты динамической вязкости равны: с;
с;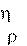 где – коэффициент вязкости;
где – коэффициент вязкости;



