
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематическая часть основной задачи механики
§1. Нормальное и тангенциальное ускорение Пусть материальная точка движется по произвольной криволинейной тра- ектории (рис. 3.1) с переменной по модулю скоростью. В этом случае за счет криволинейности траектории скорость будет изме- няться по направлению, кроме того, у скорости изменяется ее модуль. Для ха- рактеристики такого движения полное ускорение удобно представить в виде суммы двух составляющих: нормального ускорения, направленного перпенди- кулярно скорости, и тангенциального ускорения, направленного вдоль вектора скорости. Введем единичный вектор e v, направленный вдоль вектора скорости:
Рис. 3.1
Тогда для ускорения из определения (2.7) и рис. 3.1 следует:
a v ev v
(3.1) (по правилу нахождения производной от произведения). Первый член, нормальное ускорение,
показывает быстроту изменения направления скорости. Второй член, тангенциальное ускорение,
направлен вдоль скорости и показывает быстроту изменения ее модуля.
(3.2)
(3.3)
a . (3.3а) Направление и величину нормального ускорения найдем для частного слу- чая равномерного движения материальной точки по окружности (рис. 3.2а, 3.2б, 3.2в):
n
R s
v(t1)
ev (t2) ev (t1)
s Рис. 3.2б R
ev (t2) e v (t1)
v(t2) ev (t2) ev ev Рис. 3.2а Рис. 3.2в
t2 t1 переместилась из начального положения
R
a n dt v. (3.2а)
показывает изменение направления вектора ско-
по вектору n, перпендикулярному вектору
значит угол между ev и стремится к). Модуль вектора
здесь n - единичный вектор нормали к скорости, n
в формулу 3.2а, при
a n v
v
t t 0 t R t 0
. (3.4а) Для движения по произвольной кривой радиус кривизны траектории R не будет величиной постоянной. На рис. 3.3 изображены векторы скорости, нормального, тангенциального и полного ускорения для этого случая. Вектор a n направлен, как и вектор n, к локальному центру кривизны траектории.
следует из (3.3), равно производной от модуля скорости по времени: a v. Модуль полного ускорения вычисляется по теореме Пифагора:
v(t)
ev
a(t) an a n R
n ev v Рис. 3.3 §2. Прямолинейное равнопеременное движение При прямолинейном движении траектория – прямая линия. Выберем сис- тему координат так, чтобы траектория материальной точки совпадала с осью х. Тогда положение тела в пространстве можно задать одной координатой – x(t). Зависимость x(t) можно получить, проинтегрировав первую из формул (2.2), записанную в виде:
Возьмем определенный интеграл от нуля до t от обеих частей этого равен- ства:
xo 0
Интеграл в левой части равенства берется так же, как и при интегрирова- нии формулы (2.11). В результате интегрирования получим:
t
0
(3.5)
Для того, чтобы взять интеграл в правой части равенства (3.5), нам необ- ходимо знать зависимость vx ( t ). Ее мы найдем, применив к нашему случаю
или x
axdt.
Проинтегрируем последнее равенство:
vo t
0 t
0
Так как ax const (движение равнопеременное), то ускорение ах можно
откуда для
vx (t) следует: vx0 ax (t 0) ax t,
vx0 ax t. (3.6)
X(t) t
0
x t)dt x0
t
0
t
0
0 x tdt
x0 vx 0 t
Оставшийся интеграл табличный, он равен:
Tdt . 0 2
v0 t . (3.7)
ния. Здесь мы, как это обычно делают, опустили индексы y скорости и ускоре-
Если за время движения знак скорости v(t) в формуле (3.6) не меняется
x0,
выражая x ( t ) x0 из (3.7) для пройденного пути s, при выполнении отмечен-
S(t)
(3.8)
Если направление движения меняется, для нахождения пройденного пути все время движения и весь путь нужно разбить на промежутки, в течение кото- рых знак скорости постоянен. Затем по формуле (3.8) найти отрезки пройден- ного пути, после чего их сложить. §3. Как решается основная задача механики материальной точки для произвольного движения Рассмотрим сначала прямолинейное движение с переменным ускорением. Положение тела по-прежнему задается одной координатой – x(t). Но ускорение,
ax ( t ) нам известна, то как и в предыдущем параграфе, из (2.7) получим:
Однако теперь ускорение dvx ax ( t ) ax (t)dt.
Интегрируя dvx, получим:
vx (t) = v0 + 0
(3.9) Затем vx (t) из (3.9) следует подставить в (3.5), и задача нахождения x(t), в принципе, решена. Решение основной задачи механики для произвольного движения матери- альной точки в трехмерном пространстве сводится к нахождению только что описанным способом трех зависимостей: x(t), y(t), z(t). Как видно из прово- дившихся рассуждений, для решения этой задачи необходимо знать три компо- ненты ускорения (a x (t), a y (t), a z (t)), три значения начальных скоростей (v0x, v0 y, v0z) и начальных координат материальной точки: x0, y0, z0. Использование векторных обозначений позволяет все это сформулировать короче: для нахождения зависимости условия ( v0 и r0 ). r ( t ) необходимо знать a ( t ) и начальные Таким образом, состояние материальной точки в любой момент времени t
полностью определяют две векторные величины: вектор скорости v ( t ) и ра- диус-вектор r ( t ). Вектор ускорения a ( t ) определяет зависимость состояния материальной точки от времени. Вопрос нахождения зависимости ускорения от времени –
a ( t ) – лежит за пределами кинематики. Этим занимается следующий раздел механики – дина- мика. Здесь отметим, что при решении основной задачи механики для системы взаимодействующих частиц ускорение обычно зависит от взаимных расстоя- ний между частицами, которые, в свою очередь, зависят от времени. Но в этом случае ясно, что явную зависимость ускорения от времени нельзя получить, по- ка не решена основная задача механики. В таких случаях на основе основного закона динамики материальной точки – второго закона Ньютона – можно полу- чить систему дифференциальных уравнений, в которых неизвестными величина- ми являются зависимости координат материальных точек системы от времени. ИТОГИ ЛЕКЦИИ № 3 1. При произвольном криволинейном движении ускорение удобно разло- жить на две составляющие: нормальное и тангенциальное ускорение (рис. 3.3)
2. Нормальное ускорение a n определяет быстроту изменения направления скорости и направлено перпендикулярно скорости (см. (3.2), (3.4), рис. 3.3). Его модуль:
здесь R – локальный радиус кривизны траектории. 3.
a = dv. τ dt
4. Модуль полного ускорения может быть найден по формуле:
5. Для прямолинейного равнопеременного движения зависимости скорости v и координаты х от времени t даются следующими формулами ((2.10), (2.11)):
at,
6. Путь s при движении с постоянным ускорением в одном направлении находится по следующей формуле:
v0 t .
7. материальной точки в трехмерном пространстве – нахождения r ( t ) - необхо- димо знать a ( t ) и начальные условия: v0 и r0 (§ 3). 8. Состояние материальной точки в любой момент времени определяется ее радиус-вектором r ( t ) и вектором ее скорости v(t). ЛЕКЦИЯ № 4
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.148 с.) |


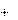 ev v
ev v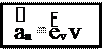
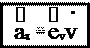
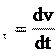 Модуль тангенциального ускорения равен, как следует из (3.3):
Модуль тангенциального ускорения равен, как следует из (3.3):
 ev (t1)
ev (t1) ev
ev


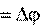
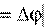
 Пусть точка за время t
Пусть точка за время t
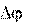
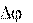 в конечное. При этом радиус R повернется на угол. По определению ради- анной меры угла измеряется отношением длины дуги к радиусу:
в конечное. При этом радиус R повернется на угол. По определению ради- анной меры угла измеряется отношением длины дуги к радиусу: s.
s.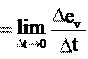 При равномерном движении по окружности скорость меняется по направ- лению, но не меняется по величине. Следовательно, тангенциальное ускорение равно нулю. Чтобы найти нормальное ускорение, воспользуемся формулой (3.2), которую запишем, применив определение производной, в следующем ви- де:
При равномерном движении по окружности скорость меняется по направ- лению, но не меняется по величине. Следовательно, тангенциальное ускорение равно нулю. Чтобы найти нормальное ускорение, воспользуемся формулой (3.2), которую запишем, применив определение производной, в следующем ви- де: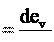
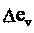 На рис. 3.2б вектор рости за промежуток времени
На рис. 3.2б вектор рости за промежуток времени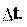
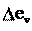 Рисунки 3.2б и 3.2в показывают, как изменяется направление вектора
Рисунки 3.2б и 3.2в показывают, как изменяется направление вектора
 при совершении предельного перехода (t 0).
при совершении предельного перехода (t 0).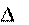 Направлен ev, при
Направлен ev, при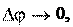
 v: (
v: (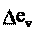
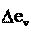 , как следует из рис. 3.2в, равен в пределе
, как следует из рис. 3.2в, равен в пределе
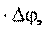
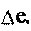 Следовательно, при t 0 для вектора выражение:
Следовательно, при t 0 для вектора выражение: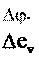 , можно записать следующее
, можно записать следующее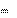 n
n


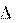 Теперь подставим полученное выражение для этом запишем как отношение S/R:
Теперь подставим полученное выражение для этом запишем как отношение S/R:


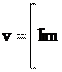
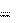 2
2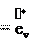 ev
ev
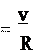
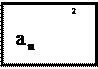 Нормальное ускорение направлено по нормали к скорости, его модуль равен:
Нормальное ускорение направлено по нормали к скорости, его модуль равен: Тангенциальное ускорение направлено так же, как скорость, и по модулю, как
Тангенциальное ускорение направлено так же, как скорость, и по модулю, как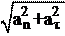 a= .
a= .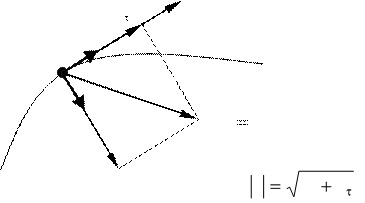 a
a

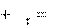 n v2
n v2 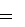 dx vxdt.
dx vxdt.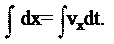 x(t) t
x(t) t x(t) x0
x(t) x0 vx dt.
vx dt.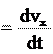 определение ускорения (2.7). Так как наше движение одномерное, то из (2.7) и (2.9) следует, что
определение ускорения (2.7). Так как наше движение одномерное, то из (2.7) и (2.9) следует, что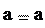
 dvx
dvx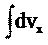 v(t)
v(t)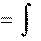 a x dt
a x dt
 a x dt.
a x dt. вынести за знак интеграла. Оставшиеся интегралы мы уже научились брать (см. (2.10) и (3.5)), после интегрирования имеем:
вынести за знак интеграла. Оставшиеся интегралы мы уже научились брать (см. (2.10) и (3.5)), после интегрирования имеем:
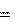 vx (t)
vx (t)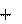 Теперь из (3.5) и (3.6) для x(t) получим:
Теперь из (3.5) и (3.6) для x(t) получим: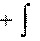
 x0 (vx 0
x0 (vx 0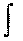 t
t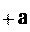 t
t vx 0dt
vx 0dt t
t
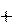
 0
0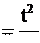
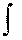 t
t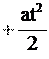 С учетом этого, окончательная формула для зависимости координаты тела х от времени t для равнопеременного движения приобретает следующий вид:
С учетом этого, окончательная формула для зависимости координаты тела х от времени t для равнопеременного движения приобретает следующий вид:
 x(t) x0
x(t) x0 (т.е. не меняется направление движения), то из (3.7) можно найти пройденный путь. Действительно, при движении в одном направлении путь:
(т.е. не меняется направление движения), то из (3.7) можно найти пройденный путь. Действительно, при движении в одном направлении путь:
 s x(t)
s x(t) ного выше условия, получим:
ного выше условия, получим: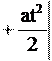
 v0 t .
v0 t .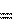 в отличие от предыдущего случая, не постоянно: ax ax ( t ). Если функция
в отличие от предыдущего случая, не постоянно: ax ax ( t ). Если функция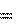 мы не можем выносить за знак интеграла.
мы не можем выносить за знак интеграла.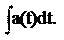 t
t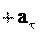
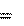 a an .
a an .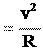 an ,
an ,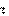 Тангенциальное ускорение a показывает быстроту изменения модуля скорости и направлено вдоль скорости (см. (3.3), рис. 3.3). Его модуль равен производной от модуля скорости по времени (3.3):
Тангенциальное ускорение a показывает быстроту изменения модуля скорости и направлено вдоль скорости (см. (3.3), рис. 3.3). Его модуль равен производной от модуля скорости по времени (3.3):
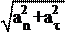 a= .
a= .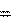 v(t) v0
v(t) v0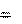 x(t) x 0
x(t) x 0
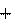 v0 t .
v0 t . s(t)
s(t)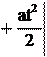 Для решения основной задачи механики при произвольном движении
Для решения основной задачи механики при произвольном движении


