Построение дерева решений и порождающих правил

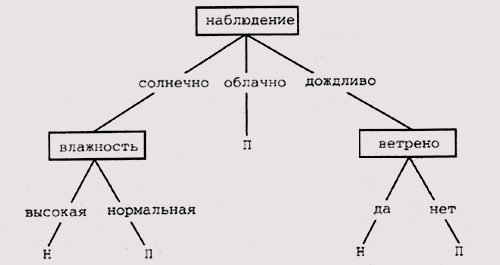
Правила являются не единственно возможным способом представления информации о концептах в виде пар- "атрибут-значение" для целей классификации. Альтернативный метод структурирования такой информации — использование дерева решения. Существуют эффективные алгоритмы конструирования таких деревьев из исходных данных. Мы обсудим их в разделе 20.3.1.

За последние 30 лет создано довольно много систем обучения, в которых использована эта методика. Среди них системы CLS [Hunt et al., 1966], ID3 [Quinlan, 1979], ACLS [Paterson and Niblett, 1982], ASSISTANT [Kononenko et al., 1984] и IND [Buntine, 1990]. Система ACLS (развитие системы ID3) стала базовой для множества коммерческих экспертных систем, таких как Expert-Ease и RuleMaster, которые нашли широкое применение в промышленности. Несколько подробнее об алгоритме работы системы ID3 будет рассказано в разделе 20.3.2.

Программный комплекс С4.5 [Quinlan, 1993] использует алгоритмы ЮЗ и включает программу C4.5Rules. Этот модуль формирует порождающие правила, используя в качестве входной информации описание дерева решений. Подробное описание этой программы имеется в технической литературе, а потому мы не будем останавливаться на ней в данной книге. В последней версии этой системы, С5.0, реализована еще более тесная интеграция форматов представления деревьев решений и правил

Структура дерева решений

Дерево решений представляет один из способов разбиения множества данных на классы или категории. Корень дерева неявно содержит все классифицируемые данные, а листья — определенные классы после выполнения классификации. Промежуточные узлы дерева представляют пункты принятия решения о выборе или выполнения тестирующих процедур с атрибутами элементов данных, которые служат для дальнейшего разделения данных в этом узле.

В работе [Quinlan, 1993] дерево решений определено как структура, которая состоит из

узлов-листьев, каждый из которых представляет определенный класс;

Узлов принятия решений, специфицирующих определенные тестовые процедуры, которые должны быть выполнены по отношению к одному из значений атрибутов; из узла принятия решений выходят ветви, количество которых соответствует количеству возможных исходов тестирующей процедуры.

Можно рассматривать дерево решений и с другой точки зрения: промежуточные узлы дерева соответствуют атрибутам классифицируемых объектов, а дуги — возможным альтернативным значениям этих атрибутов. Пример дерева представлен на рис. 20.2.

На этом дереве промежуточные узлы представляют атрибуты наблюдение, влажность, ветрено. Листья дерева промаркированы одним из двух классов П или Н. Можно считать, что П соответствует классу позитивных экземпляров концепта, а Н — классу негативных. Например, П может представлять класс "выйти на прогулку", а Н — класс "сидеть дома".

Хотя очевидно, что дерево решений является способом представления, отличным от порождающих правил, дереву можно сопоставить определенное правило классификации, которое дает для каждого объекта, обладающего соответствующим набором атрибутов (он представлен множеством промежуточных узлов дерева), решение, к какому из классов отнести этот объект (набор классов представлен множеством значений листьев дерева). В приведенном примере правило будет относить объекты к классу П или Н. Можно прямо транслировать дерево в правило, показанное ниже:

если наблюдение = облачно

v

наблюдение = солнечно &

влажность = нормально

v

наблюдение = дождливо &

ветрено = нет то П

Рис. 20.2. Дерево решений (заимствовано из [Quinlan, 1986, a])

Единственное приведенное правило, созданное непосредственно после преобразования дерева, можно разделить на три отдельных правила, которые не требуют использования логической дизъюнкции, а затем представить каждое из них на языке описания порождающих правил, например CLIPS:

if наблюдение = облачно

Then П

if наблюдение = солнечно &

влажность = нормально then П

if наблюдение = дождливо &

ветрено = нет then П

Причина, по которой предпочтение иногда отдается деревьям решений, а не порождающим правилам, состоит в том, что существуют сравнительно простые алгоритмы построения дерева решений в процессе обработки обучающей выборки, причем построенные деревья могут быть использованы в дальнейшем для корректной классификации объектов, не представленных в обучающей выборке. Алгоритм системы ID3, который используется для построения дерева по обучающей выборке, мы рассмотрим в следующем разделе. Этот алгоритм достаточно эффективен с точки зрения количества вычислительных операций, поскольку объем вычислений растет линейно по отношению к размерности проблемы.

В табл. 20.2 показана обучающая выборка, которая использовалась для формирования дерева на рис. 20.2.

Таблица 20.2. Обучающая иыборка (заимствовано us [Quinlan, 1986,a])

	Номер	Наблюдение	Температура	Влажность	Ветрено	Класс
	1	Солнечно	Жарко	Высокая	Нет	Н
	2	Солнечно	Жарко	Высокая	Да	Н
	3	Облачно	Жарко	Высокая	Нет	п
	4	Дождливо	Умеренно	Высокая	Нет	п
	5	Дождливо	Холодно	Нормальная	Нет	п
	6	Дождливо	Холодно	Нормальная	Да	Н
	7	Облачно	Холодно	Нормальная	Да	п
	8	Солнечно	Умеренно	Высокая	Нет	Н
	9	Солнечно	Холодно	Нормальная	Нет	п
	10	Дождливо	Умеренно	Нормальная	Нет	п
	11	Солнечно	Умеренно	Нормальная	Да	п
	12	Облачно	Умеренно	Высокая	Да	п
	13	Облачно	Жарко	Нормальная	Нет	п
	14	Дождливо	Умеренно	Высокая	Да	Н

Читатель может самостоятельно проверить, насколько корректно классифицируется каждый из 14 экземпляров, представленных в этой выборке. Обратите внимание на то, что атрибут температура в дереве отсутствует, поскольку он оказался излишним при выполнении классификации.