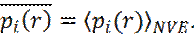Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эргодичность системы многих частицСодержание книги
Поиск на нашем сайте
Основной постулат статической механики наносистем: каждое квантовое состояние может быть занято системой с равной вероятностью. Тогда, среднее системы частиц определяется, как среднее, по ансамблю состояний системы. Но в реальном эксперименте мы измеряем какую-либо величину в течение определенного промежутка времени, и в результате получаем среднее значенип за этот промежуток. Предположим, что мы хотим рассчитать среднюю плотность жидкости, на растоянии r от некоторого атома i – pi(r).С течением времени, координаты атомов меняются и, следовательно, будет меняться плотность вокруг атома i. В методе молекулярной динамики рассчитывается усредненная по времени плотность
В выражении (18) предполагается, что
В предельном случае бесконечного количества начальных условий возможно поменять местами усреднение по начальным условиям и усреднение по времени, как не зависящие друг от друга операции. Тогда обозначая через < … > среднее по начальным условиям (ансамблю), получаем:
Из уравнения (20) следует, что усреднение по начальным координатам в фазовом пространстве эквивалентно усреднению по времени по траектории в фазовом пространстве. В связи с этим, можно опустить усреднение по времени в формуле (20) и записать:
Из последней формулы следует: - при вычислении средней величины функции координат и импульсов системы многих частиц можно вычислять эту среднюю величину с помощью усреднения по времени (метод молекулярной динамики), либо с помощью усреднения по ансамблю (метод Монте-Карло). Системы многих частиц, для которых справедливо соотношение (21) называются эргодичными. Контрольное задание 1.
Рассмотрим систему А, состоящую из подсистем А1 и А2 , для которых Ω1 = 1020 и Ω2 = 1022. Чему равно число конфигураций в объединенной системе? Вычислить также энтропии S, S1 , S2 . Контрольное задание 2.
Во сколько раз увеличится число доступных конфигураций при расширении на 0,001% 10 м3 воздуха, при постоянной температуре, находящегося при давлении 1,0 атм и температуре 300 К? Уравнение состояния: PV = nRT. При изотермическом расширении газа в пустоту:
ΔS = nR ln(V2 / V1), т.к. T dS = dU + P dV и PV = nRT. S = kB ln Ω; kB = 1,38 10-23 Дж/K; R = 8,31 Дж/(моль К); 1 атм = 105 Па. Глава 3. МОДЕЛИ КВАНТОВЫХ НАНОСИСТЕМ
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.152.189 (0.005 с.) |

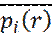 системы N атомов, в объеме V, при постоянном значении полной энергии Е:
системы N атомов, в объеме V, при постоянном значении полной энергии Е: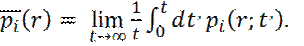 (18)
(18)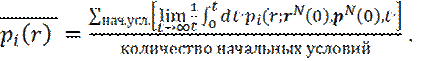 (19)
(19)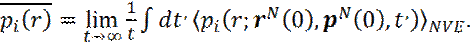 (20)
(20)