
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В химической технологии, фармацевтике и биотехнологииСодержание книги
Поиск на нашем сайте
М. Б. Глебов, В.А. Налетов
МОДЕЛИРОВАНИЕ НАНОПРОЦЕССОВ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ, ФАРМАЦЕВТИКЕ И БИОТЕХНОЛОГИИ
Утверждено Редакционным советом университета в качестве учебного пособия
Москва 2020 УДК 661.124 ББК 35.113 Г53 Рецензенты: Доктор технических наук, заведующий кафедрой процессов и аппаратов Российского химико-технологического университета им. Д.И. Менделеева, профессор Л. В. Равичев Доктор технических наук, заместитель директора по научной работе Научного центра «Малотоннажная химия», профессор А. М. Бессарабов
Глебов М. Б., Налетов В.А. Г53 Моделирование нанопроцессов в химической технологии, фармацевтике и биотехнологии: учебн. пособие / М. Б. Глебов, В.А. Налетов. __ М.: РХТУ имени Д. И. Менделеева, 2020. __ 85 с. ISBN 978-5-7237-1708-4
Излагаются принципы математического описания и моделирования основных нанопроцессов в химической технологии, фармацевтике и биотехнологии. На конкретных примерах показано использование метода математического моделирования для расчётов процессов на наноуровне, включая при этом не только разработку их математических моделей, но и алгоритмов компьютерного моделирования. Предназначено для бакалавров, обучающихся по направлению 28.03.02 – Наноинженерия, а также для магистров, аспирантов, инженерно-технических и научных работников, занимающихся вопросами исследования и моделирования нанопроцессов.
УДК 661.124 ББК 35.113 ISBN 978-5-7237-1708-4 © Российский химико_технологический университет имени Д. И. Менделеева, 2020 © Глебов М.Б., Налетов В.А. 2020
Оглавление ВВЕДЕНИЕ..................................................... 4 Глава 1. МОЛЕКУЛЯРНОЕ РАССМОТРЕНИЕ НАНОСИСТЕМ...... 5 Глава 2. РОЛЬ СТАТИСТИЧЕСКОЙ МЕХАНИКИ В МОДЕЛИРОВАНИИ НАНОСИСТЕМ ........................... 17 Глава 3. МОДЕЛИ КВАНТОВЫХ НАНОСИСТЕМ ................ 24 Глава 4. ДВИЖЕНИЕ НАНОЧАСТИЦ ВО ВНЕШНЕМ ПОЛЕ....... 36 Глава 5. МОДЕЛИРОВАНИЕ ВОДОРОДНО ПОДОБНЫХ АТОМОВ . 47 Глава 6. МЕТОД МОНТЕ-КАРЛО ДЛЯ МОДЕЛИРОВАНИЯ НАНОСИСТЕМ........................................ .... .. 58 Глава 7. МЕТОД МОЛЕКУЛЯРНОЙ ДИНАМИКИ ДЛЯ МОДЕЛИРОВАНИЯ НАНОСИСТЕМ............................ 69 ЗАКЛЮЧЕНИЕ.............................................. . 81 БИБЛИОГРАФИЧЕСКИЙ СПИСОК.............................. 82
ВВЕДЕНИЕ Одной из основных задач химической технологии является создание новых высокоэффективных процессов и совершенствование уже действующих. Её решение возможно только с помощью разработки и использования систем моделирования, автоматизированного проектирования и оптимизации химико-технологических процессов. Системы автоматизированного проектирования и моделирующие пакеты прикладных программ активно внедряются в проектных, научно-исследовательских институтах, в конструкторских бюро, в высших учебных заведениях. Их развитие обусловлено растущими требованиями к качеству химической продукции, материалов и технологий. В основе этих автоматизированных систем лежит бурно развивающийся метод математического моделирования – изучение свойств объекта на математической модели. Теоретические основы химической технологии как авангард развития химической и смежных отраслей промышленности будут опираться наряду с необходимыми экспериментальными исследованиями процессов и на метод математического моделирования, рассматриваемый в настоящем пособии. Данное пособие не претендует на полное изложение моделей разнообразных нанопроцессов химической технологии и биотехнологии. Из-за ограниченного объёма книги автор счел возможным не включать в неё ряд разделов, посвященный анализу и математическому моделированию фармацевтических процессов, которые обычно рассматриваются в специальной литературе. Тем не менее автор надеется, что будет достигнута основная цель книги – привить студентам навыки активного использования метода математического моделирования для решения задач расчёта, оптимизации и проектирования нанопроцессов в химической технологии и биотехнологии. Авторы с признательностью примет все пожелания и замечания читателей, касающиеся предлагаемого учебного пособия.
Глава 1. МОЛЕКУЛЯРНОЕ РАССМОТРЕНИЕ НАНОСИСТЕМ Распределение Больцмана Пусть имеются две равновесные области, в которых молекулы сорта i имеют собственную энергию μi1 и μi2. Тогда равновесные концентрации молекул сорта i будут связаны хорошо известным распределением Больцмана:
Или
Величина μ известна, как химический потенциал.
Основные понятия и математический аппарат квантовой механики
В квантовой механике, в силу соотношения неопределенности Гейзенберга, классические определения координат, импульса, энергии частиц теряют смысл. Вводится волновая функция Ψ(r, t), являющаяся комплексной величиной, позволяющая вычислить остальные характеристики частицы. Волновая функция - Ψ(r, t), позволяет находить вероятностные характеристики всех параметров микрочастиц. Квадрат модуля волновой функции | Ψ |2, для элемента пространства, объемом dV, определяет вероятность нахождения микрочастицы в данном объеме:
где Ψ* - комплексно-сопряженная волновая функция. Отсюда, функция плотности вероятности (вероятность нахождения микрочастицы в единице объема) P, будет равна:
Функция плотности вероятности должна удовлетворять условиям нормировки:
где интеграл берется по всему пространству, где Ψ ≠ 0. Теперь, вероятность dP нахождения частицы в интервале (X, X+dX) будет равна: Среднее значение координаты - Xср частицы, определяется как
В общем случае, среднее значение любой функции fср(X), находится по аналогичной формуле:
Уравнение Шредингера
Для частицы массой m, движущейся в поле с потенциальной энергией U(x, y, z, t) со скоростью v << c, уравнение Шредингера имеет вид:
где: Уравнение Шредингера играет в квантовой механике такую же роль, как и закон Ньютона в классической механике. Причем, Ψ –функция должна быть: 1) Конечная, непрерывная, однозначная; 2) Иметь непрерывные производные по координатам; 3) Удовлетворять условию нормировки ∫ V | Ψ |2 dV = 1. Особую роль в квантовой механике играют стационарные состояния. К ним относится, в частности, случай когда внешнее потенциальное поле не зависит от времени. В этом случае искомую волновую функцию можно искать в виде:
Где:
Получим стационарное уравнение Шредингера. Для этого подставим решение (20), в исходное уравнение Шредингера (19). Получаем:
Где Влияние размера ямы l Свободный электрон в металле, размер ямы Размер ямы соизмерим с атомом Туннелирование В этом случае, внешний потенциал
Если обозначить области до барьера, в барьере и после барьера, соответственно, I, II и III, то в областях I и III, уравнение Шредингера примет вид
а в области II
В каждой из областей, решение уравнения Шредингера имеет вид:
Постановка этого решения (8), в исходное уравнение (7), для областей I и III, дает связь волнового числа K, с общей энергией частицы E:
Или
В последнем соотношении, знак «+» соответствует волне, идущей слева направо, а знак «-» - волне, идущей справа налево. Таким образом, получаем следующее решение уравнения Шредингера, в областях I и III:
Соответственно, подстановка общего решения (9), в уравнение Шредингера, для II области (уравнение (8)), приводит к следующему характеристическому уравнению для
Или
Таким образом, после подстановки
где:
В области III, волна идет слева направо, и граничное условие при Условия сшивки решений на границе барьера имеют вид:
Таким образом, имеем 4 условия сшивки, и 5 неизвестных коэффициентов Тогда положим, коэффициент
Отношение квадратов модулей амплитуд отраженной и падающей волны:
есть коэффициент отражения, и определяет вероятность отражения частицы от потенциального барьера. Отношение квадратов модулей прошедшей и падающей волны:
Определяет вероятность прохождения частицы через барьер. С учетом системы уравнений (21) – (24), получаем:
Из последнего соотношения видно, что вероятность прохождения барьера сильно повышается с уменьшением ширины барьера a, и уменьшением Эксоненциальная зависимость квеличения вероятности туннелирования (прохождения) частицей потенциального барьера, с уменьшением ширины барьера, использована при создании сканируюшего туннельного микроскопа, где атомно-острая игла размещается на наномеровом расстоянии от поверхности проводника, что значительно увеличивает ток туннелирования через барьер игла-проводник. В этом случае, расстояние от иглы до образца играет роль ширины барьера, и при a = 0,5 нм, высоте барьера
Примеры применения метода Монте-Карло. Вычисление определенного интеграла по методу Монте-Карло
1. Вычисление определенного интеграла Традиционно при численном интегрировании отрезок [a, b] делится на равномерно распределенные узлы. Вычисляется f (x) в этих узлах и производится суммирование. Согласно методу Монте-Карло рассматривают случайную величину u, равномерно распределенную на отрезке [a, b]. Тогда функция f (u) также будет случайной величиной и ее математическое ожидание E f (u) будет:
где φ (x) - функция плотности распределения случайной величины u, равная:
Следовательно, получаем:
Откуда:
Но математическое ожидание E[f(u)] легко смоделировать, организовав случайный процесс и вычислив выборочное среднее. Таким образом вычисление определенного интеграла по методу Монте-Карло будет включать. 1. С использованием датчика случайных чисел с равномерным распределением на [a, b] образуем N значений случайной величины u. 2. Вычисляем значения случайной функции f(ui) в точке ui. 3. Вычисляем выборочное среднее
4. Вычисляем искомый интеграл:
Граничные условия
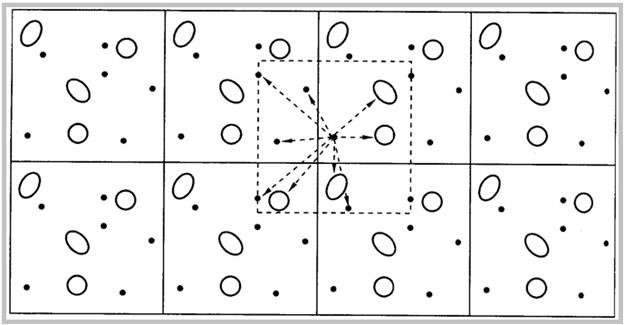
Для моделирования макросвойств объемной фазы по выборке из сотен либо тысяч частиц необходимо задать граничные условия (свободные, жесткие, периодические), которые имитируют наличие бесконечного объема вокруг выделенной N-частичной системы. Обычно это достигается путем использования периодических граничных условий. Объем, содержащий N частиц, представляет собой элементарную ячейку бесконечной периодической решетки, составленной из идентичных ячеек.
В принципе, любая выбранная частица взаимодействует со всеми другими частицами бесконечной системы и полная потенциальная энергия N частиц в любой ячейке периодической решетки равна:
где L – размер периодической ячейки (например, кубической); n – произвольный вектор из трех чисел; штрих у суммы показывает, что слагаемое с i=j должно быть исключено при n=0. Однако, на практике, мы часто работаем с короткодействующими потенциалами и, в этом случае, мы можем пренебречь межмолекулярными взаимодействиями, за пределами некоторого радиуса обрезки rc . В контексте короткодействующих потенциалов, считается, что полная потенциальная энергия данной частицы i, определяется, преимущественно, взаимодействиями с соседними частицами, находящимися внутри радиуса обрезки rc. Самый простой способ обрезки потенциалов состоит в исключении из рассмотрения всех взаимодействий, за пределами rc. В процессе моделирования используется следующий потенциал.
Инициализация
Чтобы запустить процесс моделирования, мы должны задать начальные координаты всех частиц в системе. Так как равновесные свойства системы не должны зависеть от выбора начальных условий, приемлемы любые начальные условия. Так, если мы хотим моделировать твердое состояние, конкретной модельной системы, логично подготовить эту систему, в той, конкретной кристаллической структуре, которая нас интересует. С другой стороны, если нас интересует жидкая фаза, можно приготовить систему, в любой, подходящей кристаллической структуре. Этот кристалл впоследствии растает, поскольку при любых типичных, для жидкого состояния, температуре и плотности, твердое состояние термодинамически не стабильно. Пробные смещения
Рассмотрим поступательные смещения. Вполне приемлемый метод для создания пробного смещения заключается в добавлении случайных чисел из интервала: от - ∆/2 до + ∆/2, к x, y, z - координатам частиц (центров масс молекул):
где Ranf – случайные числа, равномерно распределенные на интервале от 0 до 1. Контрольное задание на применение метода Монте-Карло. Записать алгоритм определения числа «пи», с использованием метода Монте-Карло. Задание начальных значений параметров и положения частиц (инициализация)
Чтобы инициировать процесс моделирования необходимо задать начальные положения и скорости всех частиц в системе. Положения частиц должны быть выбраны совместимыми со структурой, которую мы стремимся воспроизвести. В любом случае частицы должны располагаться так, чтобы не было заметного перекрывания атомов и молекул. Часто это достигается за счет первоначального размещения частиц в узлах кубической решетки. Для задания начальных значений скоростей, каждой компоненте скорости, у каждой частицы, приписывается произвольное значение, с равномерным распределением, в интервале [- 0,5; 0,5]. атем производится сдвиг значений скоростей таким образом, чтобы суммарный импульс в системе стал равным нулю, а также проводится перемасштабирование скоростей для достижения желаемого значения средней кинетической энергии. В состоянии теплового равновесия выполняется следующее соотношение
где v α - α -я компонента скорости частицы. Соотношение (3) может быть использовано для определения мгновенной температуры T (t), в момент времени t:
Очевидно, что возможно подогнать значение мгновенной температуры T (t), к желаемому значению T, путем перемасштабирования всех скоростей, с коэффициентом Значения скоростей сами по себе не используются при решении уравнений Ньютона. Для предсказания положения частиц на следующем шаге используются положения частиц, в настоящий (X) и предыдущий (Xm) моменты времени, вместе с информацией о силах (f), действующих на частицу. В начале моделирования, для нормального выполнения алгоритма, необходимо искусственно задать положения частиц в предыдущий момент времени. Ограничиваясь учетом только закона сохранения импульса, можно оценить предыдущее положение частиц как:
Расчет сил
Расчет сил, действующих на каждую частицу, является наиболее трудоемким этапом моделирования методом молекулярной динамики. Если рассматривать модель системы с парными аддитивными взаимодействиями, необходимо учитывать вклад всех соседей рассматриваемой частицы. Если же рассматривать только взаимодействие между некоторой частицей и ближайшим образом другой частицы (периодические граничные условия), то для системы N частиц, необходимо вычислить N ·(N -1)/2, парных взаимодействий. Первоначально, необходимо рассчитать текущее расстояние в направлении x, y, z, для каждой пары частиц. Пусть это расстояние xr . При расчете межмолекулярных взаимодействий, с периодическими граничными условиями, используют обрезку потенциала, на расстоянии rc (где rc должен быть меньше половины диаметра периодической ячейки). В этом случае мы всегда можем свести расчет межмолекулярных взаимодействий между молекулами i и j, к взаимодействию между молекулой i, и ближайшим периодическим образом молекулы j. В случае использования простой кубической ячейки, с периодическими граничными условиями, расстояние в любом направлении, между i и ближайшим периодическим образом, молекулы j, всегда должно быть меньше (по абсолютной величине), чем половина диаметра периодической ячейки. Удобный способ вычислить расстояние между i и ближайшим периодическим образом j, заключается в использовании функции ближайшего целого, nint (x), которая округляет реальное число x, до ближайшего целого. Так, имея расстояние по x, между молекулами i и j, равное xr, расстояние, по x, между i, и ближайшим образом j, вычисляется как:
гдеbox – диаметр периодической ячейки. Вычислив, таким образом, все декартовы составляющие вектора расстояния r ij, между i и ближайшим периодическим образом j, определяется величина r ij 2. Далее проверяется будет ли r ij 2 меньше квадрата радиуса обрезки rc 2. Если нет, то сразу же производится переход к следующему значению. Если какие-либо две частицы расположены достаточно близко, чтобы они могли взаимодействовать друг с другом, тогда требуется рассчитать силы между этими частицами, а также вклад в потенциальную энергию. При этом, необходимо знать выражение для потенциальной энергии взаимодействия двух частиц, на расстоянии r. Так, x -составляющая силы fx (r), будет выражаться через потенциальную энергию взаимодействия u (r), в виде:
Рассмотрим пример взаимодействия молекул в неполярной жидкости. Энергия взаимодействия двух частиц в ней описывается потенциалом Ленард- Джонса (1924 год):
В уравнении (8) ε –глубина потенциальной ямы; σ – расстояние, на котором энергия взаимодействия становится равной нулю. Пример расчета сил взаимодействия в Леннард-Джонсовской жидкости
Выведем выражение для x -составляющей силы взаимодействия молекул, на расстоянии r. Введем безразмерные координаты: В новых переменных потенциал Леннард-Джонса примет вид:
Теперь x -составляющая силы взаимодействия fx молекул будет равна:
Заключение Нанопроцессы занимают все более значимое место в химических технологиях и других смежных отраслях промышленности. Большинство из рассмотренных в настоящем учебном пособии процессов только развиваются и начинают использоваться в промышленности. И это влечет еще больший исследовательский интерес к ним. Стремление государственных и частных компаний в условиях жесткой конкуренции к внедрению новых ресурсосберегающих нанотехнологий обуславливает постоянный поиск технологических и конструктивных решений на уровне как отдельных нанопроцессов, так и всего производства в целом. К этому следует добавить постоянно растущие экологические требования, выполнение которых возможно только при условии совершенствования технологии. Сказанное объясняет жизненно важную необходимость модернизации существующих и создания новых нанопроцессов и производств с позиций последних достижений науки и техники. Здесь к числу новых направлений следует отнести внедрение совмещенных, плазмохимических процессов, процессов в сверхкритических условиях, нанобиохимических процессов и ряд других. Вместе с тем, значительный потенциал остается в направлении оптимизации и организации нанопроцессов. И его ни в коем случае нельзя принижать. Именно использование этого ресурса позволяет получить коммерческий эффект без значительных капитальных затрат, что в ряде случаев является единственным выходом поддержания конкурентноспособности производства. Таким образом, создание современной наноиндустрии, и химической в частности, обуславливает необходимость постоянных исследований в области химической технологии, биотехнологии и подготовки соответствующих кадров. Мощным инструментом в совершенствовании и создании новых нанопроцессов является математическое моделирование, дополненное необходимыми экспериментальными исследованиями. В этом смысле настоящее учебное пособие наглядно иллюстрирует практическое применение метода математического моделирования как для традиционных процессов, так и для новых нанопроцессов. Безусловно, в пособии рассмотрена лишь небольшая часть нанопроцессов. Но их систематическое изложение не является целью данного учебного пособия. Цель состоит в демонстрации метода математического моделирования для изучения, совершенствования и создания новых нанопроцессов химической технологии и биотехнологии.
Библиографический список
1. Закгейм А. Ю. Введение в моделирование химико-технологических процессов. __ М.: Химия, 1982. – 288. 2. Кафаров В. В. Методы кибернетики в химии и химической техно- логии. __ М.: Химия, 1985. – 498. 3. Кафаров В. В. Основы массопередачи. — М.: Высшая школа, 1979. – 439. 4. Кафаров В. В., Глебов М. Б. Математическое моделирование основных процессов химических производств. __ М.: Юрайт, 2019. – 403. 5. Комиссаров Ю. А., Гордеев Л. С., Вент Д. П. Процессы и аппараты химической технологии. __ М.: Химия, 2011. – 1230. 6. Левич В. Г. Физико-химическая гидродинамика. __ М.: Физматгиз, 1959. – 700. 7. Марчук Г. И. Методы вычислительной математики. __ М.: Наука, 1977. – 538. 8. Плановский А. Н., Муштаев В. И., Ульянов В. М. Сушка дисперсных материалов в химической промышленности. __ М.: Химия, 1979. – 287. 9. Праузниц Дж. М. Машинный расчет парожидкостного равновесия. __ М.: Химия, 1971. – 215. 10. Таганов И. Н. Моделирование процессов массо- и энергопереноса: нелинейные системы. __ Л.: Химия, 1979. – 208. 11. Тодес О. М., Себалло В. А., Гольцикер А. Д. Массовая кристаллизация из растворов. __ Л.: Химия, 1984. – 232. 12. Тябин Н.В. Теория равновесия и переноса в химико-технологических процессах. __ Волгоград: Волгоградский политехн. ин-т, 1983. – 122. 13. Франк-Каменецкий Д. А. Диффузия и теплопередача в химической кинетике. __ М.: Наука, 1967. – 502. 14.Практикум по основам сверхкритических флюидных технологий: учеб. пособие / Р. А. Газизов [ и др.] __ Казань: ООО “Инновационно – издательский дом “Бутлеровское наследие”; 2010. – 452.
Учебное издание
ГЛЕБОВ Михаил Борисович, НАЛЕТОВ Владислав Алексеевич
МОДЕЛИРОВАНИЕ НАНОПРОЦЕССОВ М. Б. Глебов, В.А. Налетов
МОДЕЛИРОВАНИЕ НАНОПРОЦЕССОВ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ, ФАРМАЦЕВТИКЕ И БИОТЕХНОЛОГИИ
Утверждено Редакционным советом университета в качестве учебного пособия
Москва 2020 УДК 661.124 ББК 35.113 Г53 Рецензенты: Доктор технических наук, заведующий кафедрой процессов и аппаратов Российского химико-технологического университета им. Д.И. Менделеева, профессор Л. В. Равичев Доктор технических наук, заместитель директора по научной работе Научного центра «Малотоннажная химия», профессор А. М. Бессарабов
Глебов М. Б., Налетов В.А. Г53 Моделирование нанопроцессов в химической технологии, фармацевтике и биотехнологии: учебн. пособие / М. Б. Глебов, В.А. Налетов. __ М.: РХТУ имени Д. И. Менделеева, 2020. __ 85 с. ISBN 978-5-7237-1708-4
Излагаются принципы математического описания и моделирования основных нанопроцессов в химической технологии, фармацевтике и биотехнологии. На конкретных примерах показано использование метода математического моделирования для расчётов процессов на наноуровне, включая при этом не только разработку их математических моделей, но и алгоритмов компьютерного моделирования. Предназначено для бакалавров, обучающихся по направлению 28.03.02 – Наноинженерия, а также для магистров, аспирантов, инженерно-технических и научных работников, занимающихся вопросами исследования и моделирования нанопроцессов.
УДК 661.124 ББК 35.113 ISBN 978-5-7237-1708-4 © Российский химико_технологический университет имени Д. И. Менделеева, 2020 © Глебов М.Б., Налетов В.А. 2020
Оглавление ВВЕДЕНИЕ..................................................... 4 Глава 1. МОЛЕКУЛЯРНОЕ РАССМОТРЕНИЕ НАНОСИСТЕМ...... 5 Глава 2. РОЛЬ СТАТИСТИЧЕСКОЙ МЕХАНИКИ В МОДЕЛИРОВАНИИ НАНОСИСТЕМ ........................... 17 Глава 3. МОДЕЛИ КВАНТОВЫХ НАНОСИСТЕМ ................ 24 Глава 4. ДВИЖЕНИЕ НАНОЧАСТИЦ ВО ВНЕШНЕМ ПОЛЕ....... 36 Глава 5. МОДЕЛИРОВАНИЕ ВОДОРОДНО ПОДОБНЫХ АТОМОВ . 47 Глава 6. МЕТОД МОНТЕ-КАРЛО ДЛЯ МОДЕЛИРОВАНИЯ НАНОСИСТЕМ........................................ .... .. 58 Глава 7. МЕТОД МОЛЕКУЛЯРНОЙ ДИНАМИКИ ДЛЯ МОДЕЛИРОВАНИЯ НАНОСИСТЕМ............................ 69 ЗАКЛЮЧЕНИЕ.............................................. . 81 БИБЛИОГРАФИЧЕСКИЙ СПИСОК.............................. 82
ВВЕДЕНИЕ Одной из основных задач химической технологии является создание новых высокоэффективных процессов и совершенствование уже действующих. Её решение возможно только с помощью разработки и использования систем моделирования, автоматизированного проектирования и оптимизации химико-технологических процессов. Системы автоматизированного проектирования и моделирующие пакеты прикладных программ активно внедряются в проектных, научно-исследовательских институтах, в конструкторских бюро, в высших учебных заведениях. Их развитие обусловлено растущими требованиями к качеству химической продукции, материалов и технологий. В основе этих автоматизированных систем лежит бурно развивающийся метод математического моделирования – изучение свойств объекта на математической модели. Теоретические основы химической технологии как авангард развития химической и смежных отраслей промышленности будут опираться наряду с необходимыми экспериментальными исследованиями процессов и на метод математического моделирования, рассматриваемый в настоящем пособии. Данное пособие не претендует на полное изложение моделей разнообразных нанопроцессов химической технологии и биотехнологии. Из-за ограниченного объёма книги автор счел возможным не включать в неё ряд разделов, посвященный анализу и математическому моделированию фармацевтических процессов, которые обычно рассматриваются в специальной литературе. Тем не менее автор надеется, что будет достигнута основная цель книги – привить студентам навыки активного использования метода математического моделирования для решения задач расчёта, оптимизации и проектирования нанопроцессов в химической технологии и биотехнологии. Авторы с признательностью примет все пожелания и замечания читателей, касающиеся предлагаемого учебного пособия.
Глава 1. МОЛЕКУЛЯРНОЕ РАССМОТРЕНИЕ НАНОСИСТЕМ
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.15.112 (0.018 с.) |

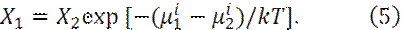
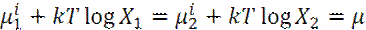
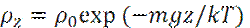 - Барометрическое распределение
- Барометрическое распределение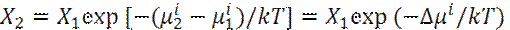 - Растворимость по Нернсту
- Растворимость по Нернсту (6)
(6)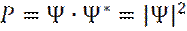 (7)
(7) , (8)
, (8)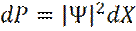 . (9)
. (9)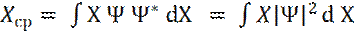 (10)
(10)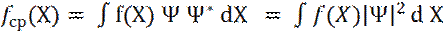 (11)
(11)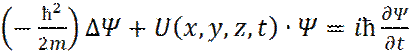 (19)
(19)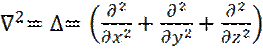 - оператор Лапласа.
- оператор Лапласа.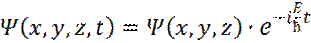 (20)
(20)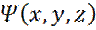 – функция координат;
– функция координат;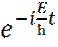 – функция t
– функция t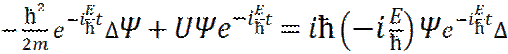 (21)
(21)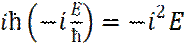
 т. е. энергетические уровни расположены так тесно, что спектр можно считать непрерывным для зоны проводимости.
т. е. энергетические уровни расположены так тесно, что спектр можно считать непрерывным для зоны проводимости. т. е. дискретные значения энергии, спектр – линейчатый.
т. е. дискретные значения энергии, спектр – линейчатый.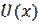 , имеет вид:
, имеет вид: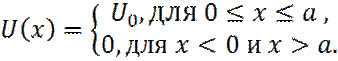 (6)
(6)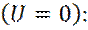
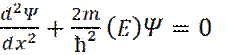 (7)
(7)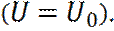
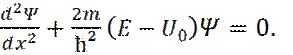 (8)
(8)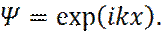 (9)
(9)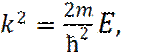 (10)
(10)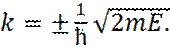 (11)
(11)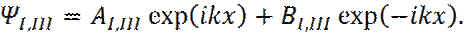 (12)
(12)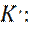
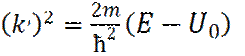 (13)
(13)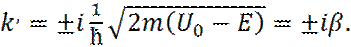 (14)
(14)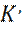 , в общее решение уравнения Шредингера (9), для области II, решение является суммой убывающей и возрастающей экспонент:
, в общее решение уравнения Шредингера (9), для области II, решение является суммой убывающей и возрастающей экспонент: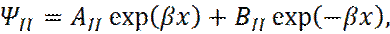 (15)
(15)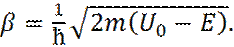 (16)
(16)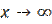 (граничное условие Зоммерфельда, определяющее единственность решения), требует, чтобы
(граничное условие Зоммерфельда, определяющее единственность решения), требует, чтобы 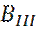 равнялось 0, в решении
равнялось 0, в решении 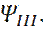
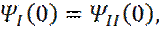 (17)
(17)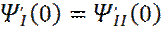 , (производные) (18)
, (производные) (18)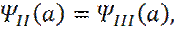 (19)
(19)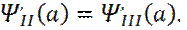 (производные) (20)
(производные) (20)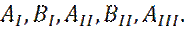 Один коэффициент получается произвольным, в силу однородности уравнения Шредингера.
Один коэффициент получается произвольным, в силу однородности уравнения Шредингера.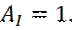 Получаем после подстановки решений
Получаем после подстановки решений 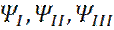 , в соотношения (17) - (20), следующее:
, в соотношения (17) - (20), следующее: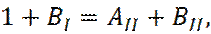 (21)
(21)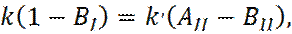 (22)
(22)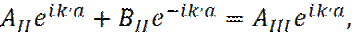 (23)
(23)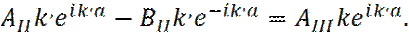 (24)
(24)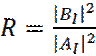 (25)
(25)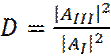 (26)
(26)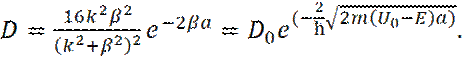 (27)
(27)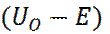 .
.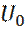 = 4 эв, создается заметный поток туннелирующих электронов, от образца к игле
= 4 эв, создается заметный поток туннелирующих электронов, от образца к игле 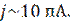
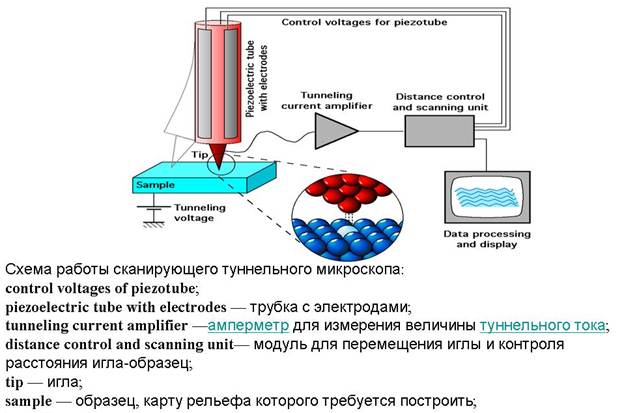




 .
. (1)
(1)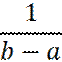
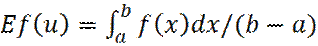 (2)
(2) (3)
(3) (4)
(4)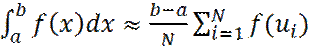 (5)
(5)
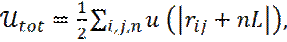 (21)
(21) (22)
(22)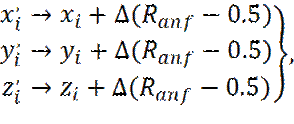 (23)
(23)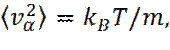 (3)
(3)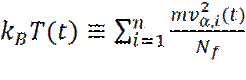 (4)
(4)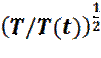 .
.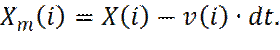 (5)
(5)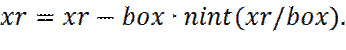 (6)
(6)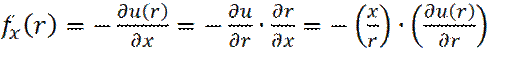 (7)
(7)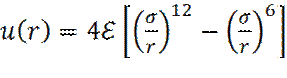 (8)
(8)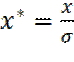 ,
, 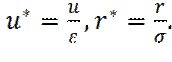
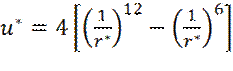 (9)
(9)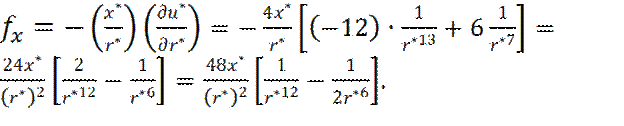 (10)
(10)


