
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частица в одномерной прямоугольной потенциальной яме с бесконечно высокими стенкамиСодержание книги
Поиск на нашем сайте
Частица движется вдоль оси x. Энергия отсчитывается от дна ямы. Яма описывается потенциальной энергией:
Уравнение Шредингера для стационарного состояния в одномерном случае:
Из граничных условий следует: 1. Бесконечно высокие стенки → частица не проникает за пределы ямы → 2. На границе ямы
3. В яме (где Дифференциальное уравнение гармонического осциллятора:
Общее решение дифференциального уравнения: Условие на границе:
т. е. уравнение Шредингера удовлетворяется только при собственных значениях Т. о. n – главное квантовое число определяет энергию уровня.
Собственным функциям Энергетический интервал между двумя соседними уровнями
Влияние размера ямы l Свободный электрон в металле, размер ямы Размер ямы соизмерим с атомом Влияние главного квантового числа n
Все остальные уровни Контрольное задание 1. Оценить значения первых двух энергетических уровней электрона в потенциальной яме размером 1 Ǻ с бесконечно высокими стенками.
Масса электрона составляет 9,1 10-31 кг.
Контрольное задание 2. Имеется проводник со свободной квантовой частицей (электроном) длиной X. Найти вероятность P нахождения частицы (электрона) на отрезке [0; Δ x ].
Глава 4. ДВИЖЕНИЕ НАНОЧАСТИЦ ВО ВНЕШНЕМ ПОЛЕ Осцилляции частиц в параболическом внешнем поле Этот случай интересен для описания осцилляций молекул во внешнем параболическом поле (яме). Пусть параболическая форма внешнего поля
Или, для молекулы, с массой m и частотой собственных колебаний
Тогда, уравнение Шредингера приобретает вид:
Аналитическое решение уравнения (3) (собственные функции), находят в виде степенного ряда. Соответствующий спектр энергий
Отметим, что энергетические уровни
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.124 (0.007 с.) |

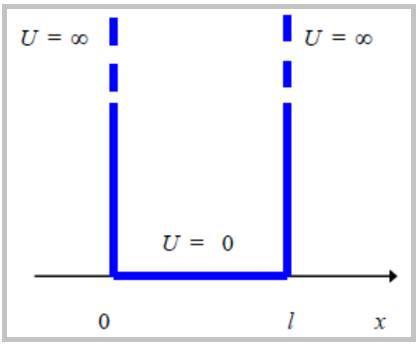
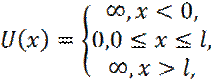 l – ширина ямы.
l – ширина ямы.
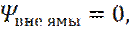
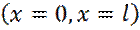 непрерывная функция
непрерывная функция 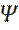 обращается в нуль:
обращается в нуль: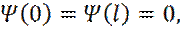
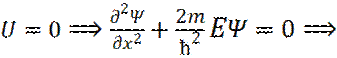

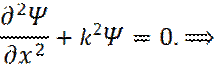
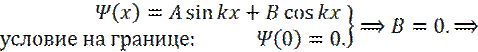
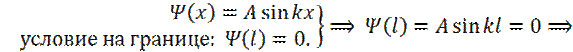
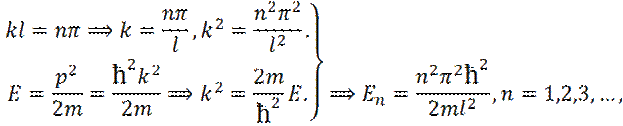
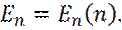
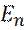 принимает дискретные значения – квантуется. Квантовые значения
принимает дискретные значения – квантуется. Квантовые значения 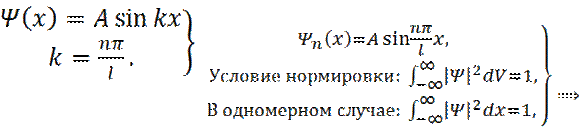
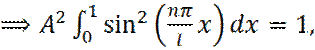 на концах промежутка интегрирования
на концах промежутка интегрирования 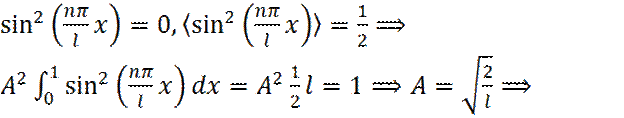
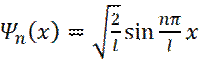 соответствуют уровни энергии
соответствуют уровни энергии 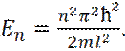
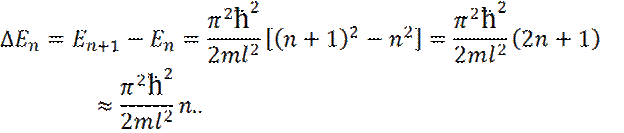
 т. е. энергетические уровни расположены так тесно, что спектр можно считать непрерывным для зоны проводимости.
т. е. энергетические уровни расположены так тесно, что спектр можно считать непрерывным для зоны проводимости. т. е. дискретные значения энергии, спектр – линейчатый.
т. е. дискретные значения энергии, спектр – линейчатый.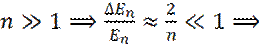 соседние уровни расположены очень тесно, можно говорить о непрерывных уровнях, т. е. о энергетической зоне (квазинепрерывные уровни).
соседние уровни расположены очень тесно, можно говорить о непрерывных уровнях, т. е. о энергетической зоне (квазинепрерывные уровни).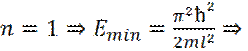 частица в потенциальной яме и не может иметь энергию, меньше
частица в потенциальной яме и не может иметь энергию, меньше 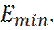
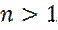 имеют
имеют 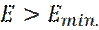
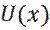 не ограничена по координате x, т. е.:
не ограничена по координате x, т. е.: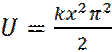 (1)
(1)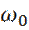 , будет:
, будет: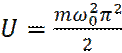 (2)
(2)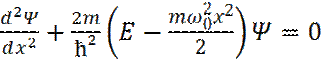 (3)
(3)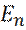 дискретен и равен:
дискретен и равен: (4)
(4)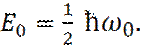 (5)
(5)


