
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь автокорреляционной функции скорости с коэффициентом диффузии (соотношение Грина-Кубо)Содержание книги
Поиск на нашем сайте
Получим выражение, связывающее коэффициент диффузии D, со скоростями частиц v i (t). За основу возьмем соотношение:
и для простоты будем рассматривать средний квадрат смещения только по одной из декартовых координат. Следует уточнить, что под смещением частицы в системе, с периодическими граничными условиями, подразумевается интеграл по времени от скорости, выделенной частицы
Если записать смещение частицы x (t), за время t, как интеграл по времени от x -составляющей скорости выделенной частицы, получим:
Величина Автокорреляционная функция скорости является равновесным свойством системы, потому что отражает связь между скоростями, осредненную по всем частицам, при движении системы частиц вдоль равновесной траектории. Поскольку равновесные свойства инвариантны относительно времени начала отсчета, автокорреляционная функция зависит только от разности (t ’ – t ’’). Следовательно, можно записать:
Подставляя (31) и (30) в уравнение (29), получаем:
Отсюда:
Из последнего выражения видна связь коэффициента диффузии D, с интегралом от автокорреляционной функции скорости. Соотношение (33) называется соотношением Грина-Кубо. Аналогичные соотношения Грина-Кубо существуют и для многих других кинетических коэффициентов, таких, как сдвиговая вязкость, теплопроводность, электропроводность и т.д. Временные корреляционные функции могут быть легко рассчитаны, в ходе метода молекулярной динамики. Соотношение Грина-Кубо для D и соотношение Эйнштейна полностью эквивалентны. Заключение Нанопроцессы занимают все более значимое место в химических технологиях и других смежных отраслях промышленности. Большинство из рассмотренных в настоящем учебном пособии процессов только развиваются и начинают использоваться в промышленности. И это влечет еще больший исследовательский интерес к ним. Стремление государственных и частных компаний в условиях жесткой конкуренции к внедрению новых ресурсосберегающих нанотехнологий обуславливает постоянный поиск технологических и конструктивных решений на уровне как отдельных нанопроцессов, так и всего производства в целом. К этому следует добавить постоянно растущие экологические требования, выполнение которых возможно только при условии совершенствования технологии. Сказанное объясняет жизненно важную необходимость модернизации существующих и создания новых нанопроцессов и производств с позиций последних достижений науки и техники. Здесь к числу новых направлений следует отнести внедрение совмещенных, плазмохимических процессов, процессов в сверхкритических условиях, нанобиохимических процессов и ряд других. Вместе с тем, значительный потенциал остается в направлении оптимизации и организации нанопроцессов. И его ни в коем случае нельзя принижать. Именно использование этого ресурса позволяет получить коммерческий эффект без значительных капитальных затрат, что в ряде случаев является единственным выходом поддержания конкурентноспособности производства. Таким образом, создание современной наноиндустрии, и химической в частности, обуславливает необходимость постоянных исследований в области химической технологии, биотехнологии и подготовки соответствующих кадров. Мощным инструментом в совершенствовании и создании новых нанопроцессов является математическое моделирование, дополненное необходимыми экспериментальными исследованиями. В этом смысле настоящее учебное пособие наглядно иллюстрирует практическое применение метода математического моделирования как для традиционных процессов, так и для новых нанопроцессов. Безусловно, в пособии рассмотрена лишь небольшая часть нанопроцессов. Но их систематическое изложение не является целью данного учебного пособия. Цель состоит в демонстрации метода математического моделирования для изучения, совершенствования и создания новых нанопроцессов химической технологии и биотехнологии.
Библиографический список
1. Закгейм А. Ю. Введение в моделирование химико-технологических процессов. __ М.: Химия, 1982. – 288. 2. Кафаров В. В. Методы кибернетики в химии и химической техно- логии. __ М.: Химия, 1985. – 498. 3. Кафаров В. В. Основы массопередачи. — М.: Высшая школа, 1979. – 439. 4. Кафаров В. В., Глебов М. Б. Математическое моделирование основных процессов химических производств. __ М.: Юрайт, 2019. – 403. 5. Комиссаров Ю. А., Гордеев Л. С., Вент Д. П. Процессы и аппараты химической технологии. __ М.: Химия, 2011. – 1230. 6. Левич В. Г. Физико-химическая гидродинамика. __ М.: Физматгиз, 1959. – 700. 7. Марчук Г. И. Методы вычислительной математики. __ М.: Наука, 1977. – 538. 8. Плановский А. Н., Муштаев В. И., Ульянов В. М. Сушка дисперсных материалов в химической промышленности. __ М.: Химия, 1979. – 287. 9. Праузниц Дж. М. Машинный расчет парожидкостного равновесия. __ М.: Химия, 1971. – 215. 10. Таганов И. Н. Моделирование процессов массо- и энергопереноса: нелинейные системы. __ Л.: Химия, 1979. – 208. 11. Тодес О. М., Себалло В. А., Гольцикер А. Д. Массовая кристаллизация из растворов. __ Л.: Химия, 1984. – 232. 12. Тябин Н.В. Теория равновесия и переноса в химико-технологических процессах. __ Волгоград: Волгоградский политехн. ин-т, 1983. – 122. 13. Франк-Каменецкий Д. А. Диффузия и теплопередача в химической кинетике. __ М.: Наука, 1967. – 502. 14.Практикум по основам сверхкритических флюидных технологий: учеб. пособие / Р. А. Газизов [ и др.] __ Казань: ООО “Инновационно – издательский дом “Бутлеровское наследие”; 2010. – 452.
Учебное издание
ГЛЕБОВ Михаил Борисович, НАЛЕТОВ Владислав Алексеевич
МОДЕЛИРОВАНИЕ НАНОПРОЦЕССОВ
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.95 (0.006 с.) |

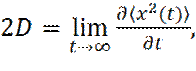 (28)
(28) (29)
(29)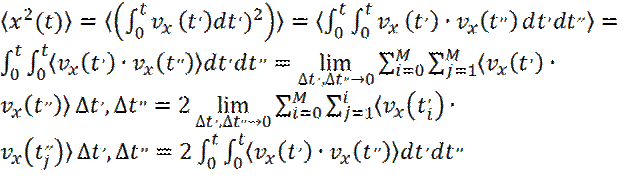 (30)
(30)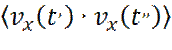 называется автокорреляционной функцией скорости. Она показывает связь скорости, в различные моменты времени t ’ и t ’’.
называется автокорреляционной функцией скорости. Она показывает связь скорости, в различные моменты времени t ’ и t ’’. (31)
(31) (32)
(32)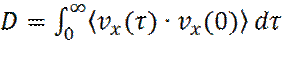 (33)
(33)


