
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пояснение к процедуре принятия или отклонения пробного шагаСодержание книги
Поиск на нашем сайте
Предположим, что пробное смещение из состояния o, в состояние n построено, причем U (n)> U (o). Тогда согласно правилу Метрополиса (11), этот пробный шаг должен принят с вероятностью:
Для того чтобы решить, принять или отклонить пробное смещение, генерируется случайное число Ranf, равномерно распределенное на интервале [0, 1]. Очевидно, что вероятность того, что Ranf меньше, чем acc (o → n), равна acc (o → n). Пробное смещение принимается, если Ranf < acc (o → n) и отклоняется в противном случае. Это гарантирует, что вероятность принять пробное смещение из o в n действительно равна acc (o → n). 6.9. Базовый алгоритм Монте-Карло (модификация Метрополиса)
Основной целью применения метода Монте-Карло, в наших задачах, является вычисление равновесных свойств наносистем. Выше было показано, что вероятность перехода системы в новое состояние, пропорциональна больцмановскому фактору exp (- β U (rN)). Соответствующий алгоритм метода Монте-Карло, в модификации Метрополиса, имеет следующий вид. 1. Выбрать частицу случайным образом и вычислить ее энергию U(rN). 2. Задать случайное смещение частицы r ‘= r + Δ и вычислить ее новую энергию U(r‘N). 3. Принять смещение rN в r ‘ N , с вероятностью:
4. Если ranf < exp (- β (U (r ‘ N) – U (rN))), то перевести систему в состояние n. В противном случае оставить систему в состоянии o. 5. Если цикл по частицам не закончился, то перейти к п. 1, выполнив предварительно расчет нового значения средней величины оцениваемого параметра. Граничные условия
Для моделирования макросвойств объемной фазы по выборке из сотен либо тысяч частиц необходимо задать граничные условия (свободные, жесткие, периодические), которые имитируют наличие бесконечного объема вокруг выделенной N-частичной системы. Обычно это достигается путем использования периодических граничных условий. Объем, содержащий N частиц, представляет собой элементарную ячейку бесконечной периодической решетки, составленной из идентичных ячеек.
В принципе, любая выбранная частица взаимодействует со всеми другими частицами бесконечной системы и полная потенциальная энергия N частиц в любой ячейке периодической решетки равна:
где L – размер периодической ячейки (например, кубической); n – произвольный вектор из трех чисел; штрих у суммы показывает, что слагаемое с i=j должно быть исключено при n=0. Однако, на практике, мы часто работаем с короткодействующими потенциалами и, в этом случае, мы можем пренебречь межмолекулярными взаимодействиями, за пределами некоторого радиуса обрезки rc . В контексте короткодействующих потенциалов, считается, что полная потенциальная энергия данной частицы i, определяется, преимущественно, взаимодействиями с соседними частицами, находящимися внутри радиуса обрезки rc. Самый простой способ обрезки потенциалов состоит в исключении из рассмотрения всех взаимодействий, за пределами rc. В процессе моделирования используется следующий потенциал.
Инициализация
Чтобы запустить процесс моделирования, мы должны задать начальные координаты всех частиц в системе. Так как равновесные свойства системы не должны зависеть от выбора начальных условий, приемлемы любые начальные условия. Так, если мы хотим моделировать твердое состояние, конкретной модельной системы, логично подготовить эту систему, в той, конкретной кристаллической структуре, которая нас интересует. С другой стороны, если нас интересует жидкая фаза, можно приготовить систему, в любой, подходящей кристаллической структуре. Этот кристалл впоследствии растает, поскольку при любых типичных, для жидкого состояния, температуре и плотности, твердое состояние термодинамически не стабильно. Пробные смещения
Рассмотрим поступательные смещения. Вполне приемлемый метод для создания пробного смещения заключается в добавлении случайных чисел из интервала: от - ∆/2 до + ∆/2, к x, y, z - координатам частиц (центров масс молекул):
где Ranf – случайные числа, равномерно распределенные на интервале от 0 до 1. Контрольное задание на применение метода Монте-Карло. Записать алгоритм определения числа «пи», с использованием метода Монте-Карло.
|
||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.57.5 (0.009 с.) |

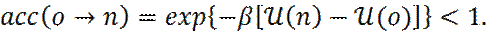
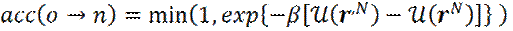 . (20)
. (20)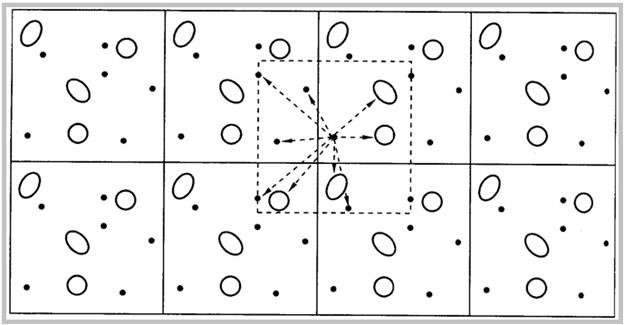
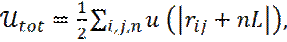 (21)
(21) (22)
(22)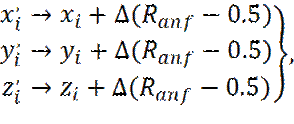 (23)
(23)


